
Как построить равнобедренный треугольник по основанию и биссектрисе: подробное руководство
Хотите построить равнобедренный треугольник, но не знаете, с чего начать? Не волнуйтесь, мы поможем вам разобраться! Для построения такого треугольника вам понадобится знать основу и биссектрису треугольника. Основание — это доступный отрезок, а биссектриса — это линия, которая делит угол пополам и пересекает противоположную сторону. Можно легко построить равнобедренный треугольник, следуя нескольким шагам. Возьмите основу и поставьте концы на некотором расстоянии друг от друга. Затем проведите биссектрису из вершины основания и учете, где она пересекает сторону треугольника. Соединив эти точки, вы получите равные стороны треугольника и, следовательно, равнобедренный треугольник. Теперь вы можете самостоятельно построить равнобедренный треугольник!
Основные понятия
Давайте разберемся с некоторыми основными понятиями, связанными с построением равнобедренного треугольника по основанию и биссектрисе. Понимание этих терминов поможет нам лучше понять процесс построения и применение данного типа треугольника в геометрии.
Равнобедренный треугольник
Равнобедренный треугольник — это треугольник, у которого два стороны равны друг другу. Иначе говоря, у равнобедренного треугольника две равные стороны и два равных угла. В равнобедренном треугольнике одна сторона называется основанием, а другие две стороны — боковыми сторонами.
Основание
Основание треугольника — это одна из его сторон, которая лежит в основании. В контексте построения равнобедренного треугольника по основанию и биссектрисе, мы будем использовать заданное основание для создания такого треугольника.
Биссектриса
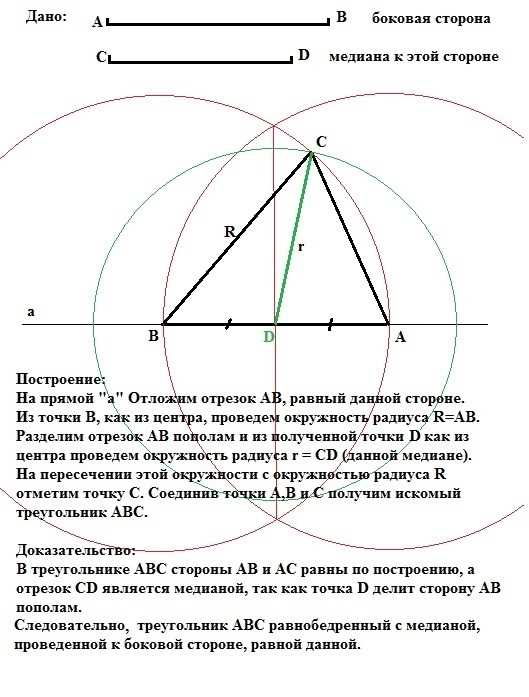
Биссектриса треугольника — это линия, которая делит внутренний угол треугольника на две равные части. В данном случае мы будем использовать биссектрису как одну из условий для построения равнобедренного треугольника.
Перпендикулярная
Перпендикулярная — это линия, которая образует прямой угол (90 градусов) с другой линией. В процессе построения равнобедренного треугольника по основанию и биссектрисе, мы будем использовать перпендикулярные линии для создания необходимых точек и пересечений.
Теперь, когда мы понимаем основные понятия, мы готовы перейти к следующему шагу — к построению равнобедренного треугольника по основанию и биссектрисе.
Равнобедренный треугольник
Для построения равнобедренного треугольника необходимо знать хотя бы две стороны или одну сторону и один угол. Если известны две стороны треугольника, равнобедренность можно проверить, сравнив длины с помощью инструментов измерения или математических вычислений. Если известна одна сторона и один угол, можно использовать тригонометрию или специальные геометрические конструкции, чтобы построить равнобедренный треугольник.
Существует несколько способов построения равнобедренного треугольника. Один из них — построение треугольника по основанию и биссектрисе угла при основании.
Для этого нужно:
- Нарисовать основание треугольника.
- С самого нижнего угла основания провести линию под углом примерно 60 градусов (или определить нужный угол с помощью угломера или транспортира).
- Провести биссектрису угла между этой линией и основанием. Биссектриса должна пересекать основание треугольника.
- Соединить точку, где биссектриса пересекает основание, с вершиной треугольника. Получится равнобедренный треугольник.
Этот метод построения можно использовать, чтобы воссоздать равнобедренные треугольники для решения задач или для творчества.
Равнобедренные треугольники широко используются в архитектуре, конструкции мостов, дизайне и других областях, где требуется равновесие и симметрия. Они также представляют собой прекрасный пример гармонии и красоты в геометрии.
Зная, как построить равнобедренный треугольник по основанию и биссектрисе, вы расширите свои знания в геометрии и сможете применять их в различных ситуациях. Используйте этот метод и наслаждайтесь процессом создания прекрасных углов и форм! Также, применив свои навыки, вы можете стать настоящим архитектором своей жизни, строящим красивые и равнобедренные треугольники на пути к успеху и достижению своих целей!
Основание треугольника
Из всей системы коммуникативной математики одна из важнейших и необходимых составляющих – треугольники, довольно фундаментальные фигуры, которыми мы все пользуемся ежедневно без сознательного понимания того, как они работают.
Основание треугольника – это ни что иное, как одна из его сторон, на которой лежит высота, или которая используется для построения биссектрисы треугольника. Другими словами, основание это та сторона треугольника, которая выступает в качестве базы для измерений и построений.
Но как найти или построить основание треугольника? В случае, когда у вас есть биссектриса треугольника, она делит основание на две равные части. В этом случае, для построения основания вам потребуется знать длину биссектрисы и ее угол с основанием. С помощью тригонометрических функций вы сможете вычислить длину основания.
| Шаги для построения основания треугольника по биссектрисе |
|---|
| 1. Измерьте длину биссектрисы треугольника |
| 2. Измерьте угол между биссектрисой и основанием треугольника |
| 3. Используя тригонометрический косинус, вычислите длину основания треугольника |
| 4. Отметьте полученную длину на основании треугольника |
Теперь у вас есть основание треугольника, которое можно использовать для различных вычислений и построений. И помните, основание не только поддерживает треугольник, но и является ключевым элементом для изучения его свойств и характеристик.
Так что, если у вас есть биссектриса треугольника и вы хотите построить его основание, следуйте приведенным выше шагам. И помните, математика — это увлекательный область знаний, которая помогает нам понять и объяснить мир вокруг нас.
Биссектриса треугольника
В геометрии биссектриса это линия, которая делит угол на две равные части. В треугольнике биссектриса проходит через вершину угла и делит противоположную сторону на две равные части. Биссектрисы могут быть внутренними, что значит они проходят внутри треугольника, или внешними, что значит они проходят за пределами треугольника.
Биссектриса треугольника имеет несколько важных свойств. Во-первых, она равноудалена от боковых сторон угла. Во-вторых, биссектрисы трех углов пересекаются в одной точке, называемой центром вписанной окружности треугольника. Это значит, что можно построить вписанную окружность, проведя биссектрисы трех углов, и она будет касаться всех трех сторон треугольника. Третье важное свойство биссектрисы — она делит противоположную сторону на отрезки, пропорциональные оставшимся сторонам треугольника.
Построить биссектрису треугольника по основанию и биссектрисе можно с помощью геометрических построений. Вот несколько шагов, которые могут помочь выполнить это построение.
- 1. На листе бумаги нарисуйте треугольник, используя линейку и карандаш. Убедитесь, что вы правильно измерили длины сторон треугольника и углы.
- 2. Найдите основание треугольника — это самая длинная сторона. Обозначьте ее точками А и В.
- 3. Найдите биссектрису основания треугольника. Для этого возьмите циркуль и сделайте две дуги с центром в точке А и В.
- 4. Проведите линию, которая соединяет пересечение этих двух дуг с вершиной треугольника. Эта линия будет биссектрисой основания треугольника.
- Нарисуйте основание треугольника любой длины на листе бумаги, используя линейку и ручку.
- Установите точку вершины треугольника, используя компас. Поместите кончик компаса на одном конце основания и нарисуйте дугу, пересекающую основание.
- Снова используйте компас, установив его на другом конце основания. Нарисуйте вторую дугу, пересекающую основание и пересекающуюся с первой дугой.
- Соедините точки пересечения дуг с основанием. Полученные отрезки будут равными и являются боковыми сторонами равнобедренного треугольника.
Теперь у вас есть построена биссектриса треугольника по основанию и биссектрисе. Вы можете использовать эту биссектрису для построения вписанной окружности и решения различных геометрических задач, связанных с треугольниками.
Шаги построения равнобедренного треугольника по основанию и биссектрисе
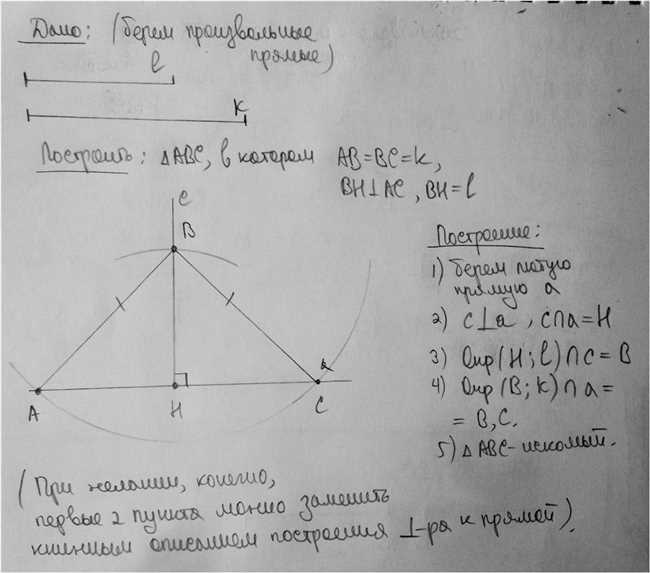
Шаг 1: Начните с рисования основания треугольника. Основание может быть изображено отрезком прямой линии на листе бумаги или на другой поверхности. Обозначьте концы основания точками A и B.
Шаг 2: Теперь вам необходимо построить биссектрису угла между сторонами основания треугольника. Для этого возьмите циркуль и на основании угла АВ отметьте точку С.
Шаг 3: Теперь необходимо найти середину стороны АС. Для этого соедините точки А и C линией, а затем проведите серединный перпендикуляр к этой линии с помощью циркуля. Пусть точка D будет серединой стороны АС.
Шаг 4: От точки D постройте перпендикуляр к основанию АВ. Пусть перпендикуляр пересекается с линией АВ в точке Е.
Шаг 5: От точки E проведите линии до точек B и C. Пусть эти линии пересекаются с биссектрисой угла АВ в точках F и G соответственно.
Шаг 6: И, наконец, постройте отрезки ФС и ГС. Теперь вы имеете треугольник АФГ, который является равнобедренным треугольником, потому что стороны АФ и ГФ равны, а углы АФГ и ГФА также равны.
Вот и все! Вы успешно построили равнобедренный треугольник по основанию и биссектрисе. Этот метод может быть использован для решения различных геометрических задач и может быть очень полезен для студентов и учащихся, изучающих геометрию. Не забывайте практиковаться и экспериментировать с различными задачами, чтобы улучшить свои навыки геометрии!
Начало работы
Построение равнобедренного треугольника по основанию и биссектрисе может показаться сложной задачей, но с помощью этого подробного руководства вы сможете легко справиться с ней. Вам потребуется всего несколько шагов и базовых знаний геометрии.
Перед началом работы, убедитесь, что у вас есть следующие материалы: линейка, компас, ручка и лист бумаги. Также рекомендуется иметь прозрачный треугольник для более точных измерений. Приступим к построению равнобедренного треугольника:
Теперь у вас есть равнобедренный треугольник, построенный по основанию и биссектрисе. Этот метод конструкции позволяет вам быстро и точно создавать данную геометрическую фигуру. Не забывайте делать точные измерения с помощью линейки и треугольника, чтобы получить наилучший результат.






