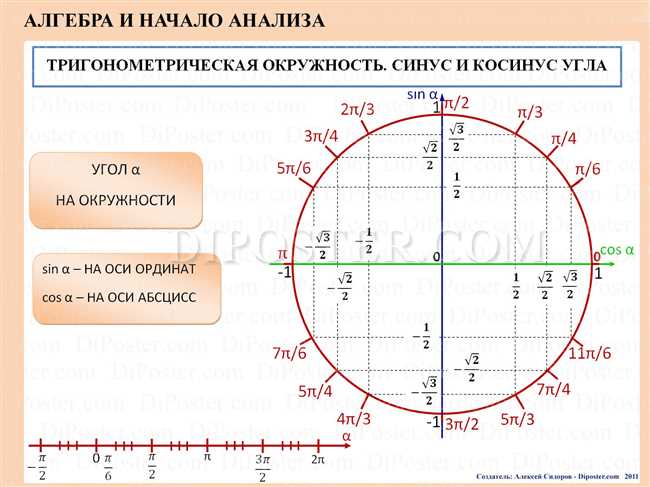
Как мы знаем, синус и косинус — это две основные тригонометрические функции, которые используются для описания отношения сторон треугольника. Когда мы рассматриваем нулевой угол (0 градусов), значения синуса и косинуса имеют особое значение.
Значение синуса нулевого угла равно 0, что означает, что противоположная сторона треугольника отсутствует. В то же время, значение косинуса нулевого угла равно 1, что означает, что прилежащая сторона треугольника равна его гипотенузе.
Таким образом, когда мы работаем с нулевым углом, синус равен 0 и косинус равен 1, что отражает его специфические геометрические свойства.
Значения синуса и косинуса нулевого угла
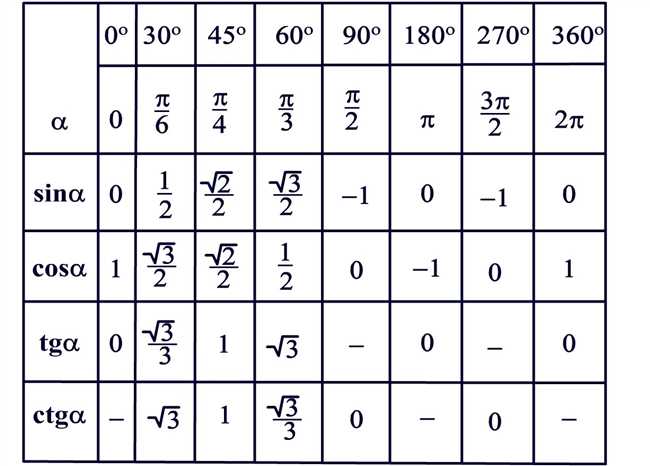
Знаете ли вы, что значение синуса и косинуса нулевого угла составляют одну из основных констант в математике? Интересно, правда? Давайте рассмотрим это ближе.
Нулевой угол — это специальный угол, который равен 0 градусам. Он обозначается как 0° или 0 radians. Это самый простой угол, который не требует вращения и не имеет никакого отклонения от начальной точки. Но, несмотря на свою простоту, нулевой угол имеет важное значение в математике и физике.
Значение синуса нулевого угла равно 0. Это означает, что синус угла, равного 0 градусам или 0 радиан, равен нулю. Он не имеет никакого смещения или отклонения от оси y. Это можно представить как точку на графике синуса, которая находится на начале координат в точке (0, 0).
А теперь давайте поговорим о косинусе нулевого угла. Значение косинуса нулевого угла также равно 1. Это означает, что косинус угла, равного 0 градусам или 0 радиан, равен единице. Он не отклоняется от оси x и равен 1 на графике косинуса.
- Синус нулевого угла равен 0
- Косинус нулевого угла равен 1
Итак, синус и косинус нулевого угла имеют фиксированные значения, и это будет всегда так независимо от выбранной единицы измерения. Это важно помнить, когда мы применяем эти функции в различных областях, таких как тригонометрия, геометрия, физика и инженерия.
Надеюсь, эта информация о значениях синуса и косинуса нулевого угла была интересной и полезной для вас! Если у вас возникли вопросы или хотите обсудить это дальше, не стесняйтесь задать вопросы — я с радостью на них отвечу!
Синус и косинус: определение и особенности
Итак, сначала давай разберемся с определением. Синус и косинус — это математические функции, которые определяют отношение длины двух сторон прямоугольного треугольника к гипотенузе. А что такое прямоугольный треугольник, спросишь ты? Это треугольник, у которого один угол равен 90 градусам, то есть прямой.
Теперь представь себе, что у нас есть прямоугольный треугольник с одним из его углов равным 0 градусам. В этом случае синус и косинус такого угла будут равны определенным значениям. Но какие же?
Для начала давай разберемся с синусом. Синус угла определяется как отношение противолежащего катета к гипотенузе. В случае нулевого угла, противолежащий катет равен нулю (ведь этот угол не имеет противолежащей стороны), а значит, синус нулевого угла также будет равен нулю.
Теперь перейдем к косинусу. Косинус угла определяется как отношение прилежащего катета к гипотенузе. В случае нулевого угла, прилежащий катет также равен нулю, поэтому косинус нулевого угла равен единице.
Теперь, когда мы знаем значения синуса и косинуса нулевого угла (синус равен нулю, а косинус равен единице), давай рассмотрим, как эти функции ведут себя в других углах.
На самом деле, синус и косинус — периодические функции. Это означает, что они повторяются через определенные интервалы. Например, синус и косинус варьируются от -1 до 1 в любом угле.
Более того, синус и косинус взаимосвязаны между собой. Если мы знаем значение синуса, мы можем найти косинус и наоборот. Интересно, верно?
В конечном итоге, синус и косинус — неотъемлемая часть математики и ее приложений. Они помогают нам понять и описать мир вокруг нас, их значения используются во многих науках и инженерных дисциплинах.
Так что теперь ты знаешь основы синуса и косинуса, и можешь показать свои знания этой увлекательной науки! Удачи!
Угол 0 градусов: особенности и свойства
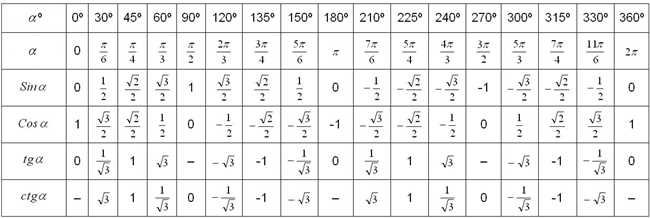
Свойства угла 0 градусов:
- Угол 0 градусов является наименьшим углом, который можно измерить.
- Угол 0 градусов имеет начало и конец на одной и той же точке, поэтому он называется нулевым углом.
Значение синуса и косинуса угла 0 градусов:
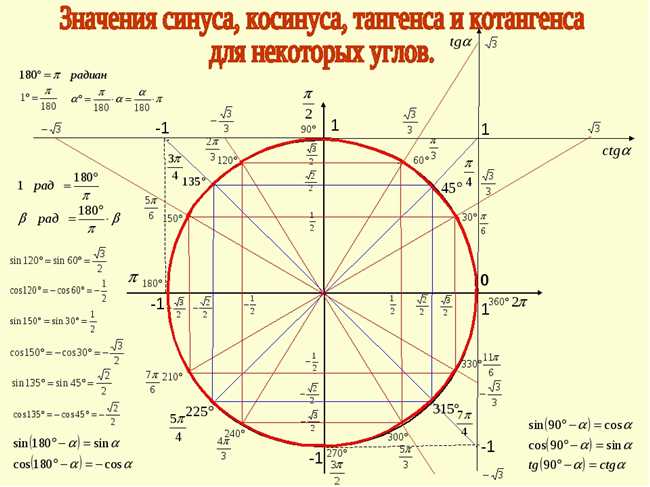
Синус и косинус — это две из основных тригонометрических функций, которые определяют отношение сторон треугольника к его углам. Значения синуса и косинуса угла 0 градусов являются ключевыми и легко запоминаются:
- Sin(0) = 0
- Cos(0) = 1
Значение синуса равно 0, что означает, что при угле 0 градусов противоположная сторона треугольника отсутствует. В то же время, значение косинуса равно 1, что указывает на то, что при угле 0 градусов катет треугольника равен гипотенузе.
Применение угла 0 градусов:
Угол 0 градусов имеет широкий спектр применений в различных областях, включая геометрию, физику и инженерию. Некоторые конкретные ситуации, в которых угол 0 градусов играет важную роль, включают:
- Определение направления векторов и вращение объектов в пространстве.
- Изучение прямых линий и их взаимного расположения.
- Расчёт мгновенной скорости и однородного движения.
Угол 0 градусов также используется как отправная точка при определении других значений тригонометрических функций и проверки различных теорем и формул, связанных с геометрией.
Значение синуса и косинуса нулевого угла
Когда говорим о значениях синуса и косинуса, можно вспомнить о прямоугольном треугольнике, в котором угол равен нулю. Вспомнишь, как построить прямоугольный треугольник? Знаешь, что это такое? Если нет, не переживай, я расскажу и об этом.
Прямоугольный треугольник — это треугольник, у которого один из углов равен 90° (прямой угол). В нем одна из сторон называется гипотенузой, а две другие — катетами.
Давай построим прямоугольный треугольник, где угол равен нулю. Получилось? Теперь представь, что стороны треугольника очень маленькие. В таком случае, катеты почти совпадают, и если мы продолжим уменьшать их размеры, они в конечном итоге совпадут полностью и образуют нулевой угол.
Теперь зададимся вопросом: что будет с синусом и косинусом при значении нулевого угла? И важно понимать, что эти функции определены для всех углов, в том числе и для нулевого.
Значение синуса нулевого угла равно 0. Почему? Потому что в нулевом угле противоположный катет (относительно угла) равен нулю, так как точки совпадают.
А что с косинусом нулевого угла? Значение косинуса нулевого угла равно 1. Почему? Потому что в нулевом угле прилежащий катет (относительно угла) равен гипотенузе, а гипотенуза всегда больше или равна катету. Поэтому косинус нулевого угла равен 1.
Итак, чтобы подытожить, значение синуса нулевого угла равно 0, а значение косинуса нулевого угла равно 1. Это необходимо помнить, так как эти значения могут использоваться в различных математических и физических задачах.
Ну что, не так уж сложно, правда? Проявишь знания синуса и косинуса нулевого угла в своей будущей работе или учебе? Был рад помочь!
Практическое применение синуса и косинуса нулевого угла
Синус и косинус нулевого угла (sin(0) и cos(0)) имеют специальные значения, которые позволяют использовать их в различных практических ситуациях. Ниже приведены несколько примеров, демонстрирующих практическое применение синуса и косинуса нулевого угла.
- Расчет длины гипотенузы прямоугольного треугольника: В прямоугольном треугольнике гипотенуза – это самая длинная сторона, которая расположена напротив прямого угла. Если один из углов этого треугольника равен нулю (т.е. прямой угол), то можно использовать значения sin(0) и cos(0), чтобы быстро вычислить длину гипотенузы. В данном случае sin(0) = 0 и cos(0) = 1, поэтому длина гипотенузы будет равна длине противоположной стороны.
- Расчет координат точки на единичной окружности: Единичная окружность – это окружность радиусом 1, центр которой находится в начале координат. Синус и косинус нулевого угла используются для определения координат точки на этой окружности. С помощью sin(0) и cos(0) можно вычислить значения координат точки на единичной окружности, находящейся на расстоянии 0 от начала координат.
- Вычисление периодических функций: Синус и косинус являются периодическими функциями, что означает, что они повторяются через определенные интервалы. Нулевой угол позволяет определить эти значения функций в начале каждого периода. Таким образом, значения sin(0) и cos(0) используются для нахождения значений функций в исходной точке.
В заключении, синус и косинус нулевого угла имеют важное практическое значение в различных областях, включая геометрию, тригонометрию и физику. Зная значения sin(0) и cos(0), можно решать разнообразные задачи, связанные с треугольниками, окружностями и периодическими функциями.
