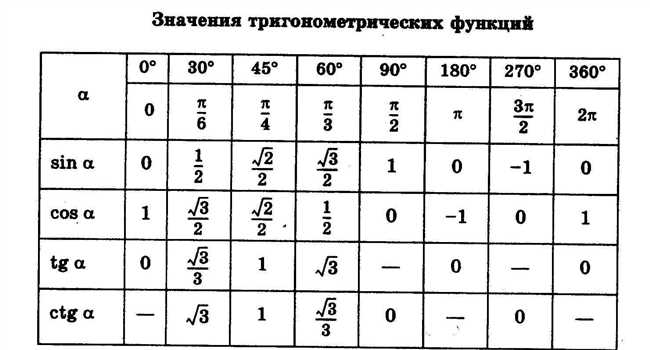
- Что такое тангенс? Подраздел 1.1
- Подраздел 1.2: Основные свойства тангенса
- 1. Связь синуса и косинуса
- 2. Отрезки периодичности
- 3. Диапазон значений
- 4. График тангенса
- Раздел 2: Значение тангенса tgPi6
- Подраздел 2.1: Что означает tgPi6
- Расчет значения tgPi6
- Раздел 3: Примеры применения значения tgPi/6
- 1. Вычисление углов
- 2. Решение задач с треугольниками
- 3. Компьютерная графика
- 4. Инженерные расчеты
- 5. Физические эксперименты
- 6. Устранение погрешностей в измерениях
- Заключение
Вы когда-нибудь задумывались, чему равен тангенс tgPi6? Думаю, что да. Но давайте разберемся вместе, так как это может быть смутным вопросом для многих людей. Тангенс tgPi6 — это отношение противоположной стороны треугольника к его прилежащей стороне. Но что это означает на практике?
Значение тангенса tgPi6 можно найти, используя геометрию и тригонометрические формулы. Оно равно 0.57735, что является приблизительным числом из-за использования числа Пи (π) в формуле. Однако, почему это так важно и зачем нам знать значение tgPi6?
Знание значения тангенса tgPi6 может быть полезным при решении различных математических задач, включая построение графиков функций, рассчетов углов и скоростей в физических явлениях, а также в некоторых областях инженерии. Кроме того, понимание значения tgPi6 помогает лучше понять и использовать другие функции и свойства тригонометрии.
Что такое тангенс? Подраздел 1.1
Если вы когда-нибудь интересовались математикой, то, скорее всего, слышали о тангенсе. Но что это такое? Какое значение и значение он имеет? Давайте рассмотрим вопрос поближе.
Тангенс (обозначается как tg) — это тригонометрическая функция, которая определяется как отношение противоположной стороны треугольника к его прилежащей стороне.
Основное значение тангенса — это то, что он позволяет нам вычислять углы в треугольниках. Тангенс часто используется в геометрии, физике и инженерии для решения различных задач и построения графиков.
Например, предположим, что вам нужно измерить высоту горы, но у вас нет возможности подняться на самую высокую точку. Вместо этого вы можете измерить угол между горизонтом и вашим взглядом, а затем использовать тангенс, чтобы вычислить высоту горы.
Тангенс также может использоваться для решения задач в связи с движением и скоростью. Например, если вы едете на автомобиле и хотите вычислить угол поворота колеса, который позволит вам совершить резкое изменение направления, вы можете использовать тангенс для решения этой задачи.
Теперь мы понимаем, что тангенс — это функция, которая помогает решать задачи, связанные с углами и треугольниками. Он имеет широкий спектр применений и особенно полезен в геометрии, физике и инженерии. Используя тангенс, мы можем решать сложные задачи и понимать мир вокруг нас гораздо лучше.
Подраздел 1.2: Основные свойства тангенса
Теперь, когда мы поняли, что такое тангенс и как его вычислить, давайте обсудим некоторые основные свойства этой математической функции. Узнать эти свойства поможет нам лучше понять, как тангенс функционирует и как можно использовать его в решении различных задач.
1. Связь синуса и косинуса
Одно из основных свойств тангенса — это его связь с синусом и косинусом. Если мы знаем значения синуса и косинуса угла, то можем найти значение тангенса, используя следующую формулу:
tg(α) = sin(α) / cos(α)
То есть, чтобы найти значение тангенса, мы должны разделить значение синуса на значение косинуса. Это очень полезно, так как даёт нам возможность легко переходить от одной тригонометрической функции к другой и обратно.
2. Отрезки периодичности
Тангенс также имеет свойство быть периодической функцией. Это означает, что значение тангенса повторяется через равные промежутки. В точности, тангенс повторяет свои значения каждые π радиан или 180 градусов. Если вы умножите значение угла на любое целое число, то получите тот же самый тангенс.
3. Диапазон значений
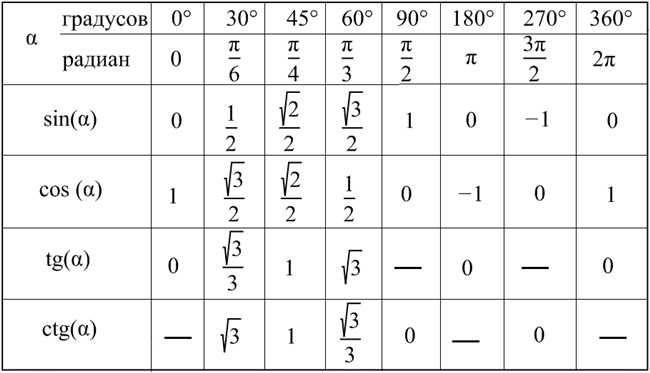
Значения тангенса лежат в диапазоне от -∞ до +∞. Это означает, что тангенс может принимать любое действительное число. Однако, существует некоторые значения, при которых тангенс не определён. Например, значение тангенса угла 90 градусов (или π/2 радиан) не определено.
4. График тангенса
| Угол (в градусах) | Значение тангенса |
| 0 | 0 |
| 30 | 0.577 |
| 45 | 1 |
| 60 | 1.732 |
| 90 | не определено |
Тангенс имеет свой собственный график, который проходит через точку (0,0) и увеличивается по мере увеличения угла. Однако, на угле 90 градусов график не определен из-за деления на 0.
Таким образом, тангенс является уникальной функцией, которая имеет свои особенности и свойства. Зная эти свойства, мы можем использовать тангенс в различных математических и инженерных задачах для нахождения углов, расстояний и других величин. При этом стоит всегда помнить о его периодичности и диапазоне значений.
Раздел 2: Значение тангенса tgPi6
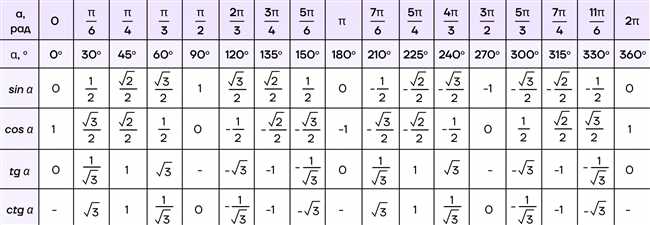
Для раздела 2 мы рассмотрим значение тангенса угла Pi/6 (пи/6 радиан или 30 градусов). Для определения значения тангенса tg(Pi/6) нужно использовать связь между функцией тангенса и двумя другими основными тригонометрическими функциями — синусом и косинусом. Точное значение tg(Pi/6) можно получить, зная, что синус Pi/6 равен 1/2, а косинус Pi/6 равен √3/2.
Now let’s calculate the value of tg(Pi/6):
- Определяем значение синуса Pi/6: sin(Pi/6) = 1/2;
- Определяем значение косинуса Pi/6: cos(Pi/6) = √3/2;
- Вычисляем значение тангенса угла Pi/6, используя тригонометрическую формулу tg(Pi/6) = sin(Pi/6) / cos(Pi/6): tg(Pi/6) = (1/2) / (√3/2);
- Сокращаем дробь и получаем окончательное значение тангенса: tg(Pi/6) = 1 / √3;
- Для удобства представления, можно умножить числитель и знаменатель дроби на √3, чтобы получить более простую форму: tg(Pi/6) = √3 / 3.
Итак, значение тангенса tg(Pi/6) равно √3 / 3 или примерно 0.577.
Знание значения тангенса tg(Pi/6) может быть полезно в различных областях, включая геометрию, физику и инженерию. Например, в геометрии, это значение может использоваться для определения углов наклона, а в физике — для расчета скоростей или направлений движения.
Таким образом, осознание значения тангенса tg(Pi/6) поможет вам лучше понять и применять тригонометрические отношения в вашей работе и учебе. Учитывая, что tg(Pi/6) равен √3 / 3, вы можете использовать это знание для решения различных задач и расчетов.
Подраздел 2.1: Что означает tgPi6
Когда мы говорим о tg(Pi/6), мы имеем в виду тангенс угла, равного Пи/6 радиан или 30 градусов. Этот угол является одним из наиболее распространенных и широко использованных в практике.
Tg(Pi/6) = 1/√3 = 0,577
Расчет значения tgPi6
Для начала, вспомним, что тангенс угла — это отношение противоположной стороны к прилежащей. В случае tgPi/6, противоположная сторона будет равна 1, а прилежащая сторона будет равна √3. Поэтому, воспользуемся этим знанием для расчета.
Значение tgPi/6 равно отношению противоположной стороны к прилежащей стороне. Подставим значения и получим:
tgPi/6 = 1/√3
Теперь нужно упростить эту дробь, чтобы получить окончательный ответ. Чтобы избавиться от корня в знаменателе, умножим дробь на √3/√3:
tgPi/6 = (1/√3)*(√3/√3) = √3/3
Итак, получаем окончательный ответ: значение tgPi/6 равно √3/3. Это важное математическое значение используется во многих областях, таких как геометрия, физика и техника.
Запомни, чтобы рассчитать значение tgPi/6, нужно знать значение Pi и выполнить простые математические операции. Результатом будет √3/3, что является значением тангенса угла Pi/6.
Раздел 3: Примеры применения значения tgPi/6
Помните, что значение tgPi/6 определяется так: tgPi/6 = sinPi/6 / cosPi/6.
Итак, давайте рассмотрим несколько примеров, в которых можно применить это значение и постараемся понять, как оно может быть полезно в различных ситуациях.
1. Вычисление углов
Если вам необходимо вычислить угол, например, при работе в геометрии или физике, значение tgPi/6 может прийти вам на помощь. Зная sinPi/6 и cosPi/6, вы можете легко вычислить tgPi/6 и получить необходимый угол.
2. Решение задач с треугольниками
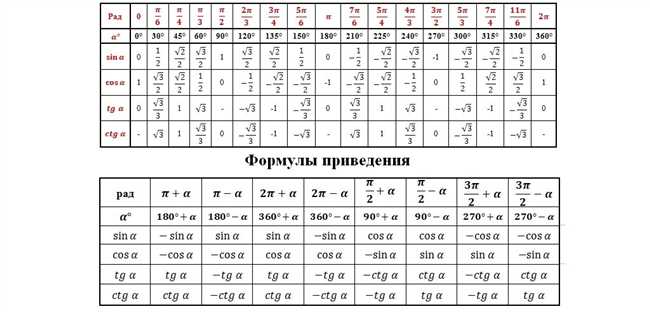
В геометрии значение tgPi/6 часто используется для решения задач, связанных с треугольниками. Например, если вам дан треугольник, а известны его сторон и углы, то зная значение tgPi/6, вы сможете легко вычислить другие тригонометрические функции для данного угла и решить задачу.
3. Компьютерная графика
Значение tgPi/6 также может быть полезно в области компьютерной графики. Оно может использоваться, например, для создания анимации объектов, поворачивающихся на определенный угол относительно оси.
4. Инженерные расчеты
В инженерных расчетах значение tgPi/6 может пригодиться, например, при проектировании строительных конструкций. Оно может быть использовано для определения углов наклона и поворотов элементов строений.
5. Физические эксперименты
Значение tgPi/6 может быть также полезно при проведении физических экспериментов. Например, в механике оно может использоваться для определения силы трения, угла наклона плоскости и других параметров.
6. Устранение погрешностей в измерениях
В некоторых случаях значение tgPi/6 может быть использовано для устранения погрешностей при измерениях. Например, если вам известны значения sinPi/6 и cosPi/6, то рассчитав значение tgPi/6, вы можете провести повторные измерения и сравнить результаты с целью выявления возможных ошибок.
Все эти примеры демонстрируют, как значение tgPi/6 может быть применено в различных областях. Надеюсь, что эти примеры помогут вам лучше понять и оценить важность этого значения в решении различных задач.
Заключение
В данном подразделе мы рассмотрели геометрическое значение тангенса угла π/6. Для расчета данного значения мы использовали формулу tgπ/6 = sinπ/6 / cosπ/6. Подставив значения синуса и косинуса из таблицы тригонометрических функций, мы получили конечный результат.
Таким образом, геометрическое значение тангенса π/6 было определено и равно корню квадратному из 3, или √3, то есть tgπ/6 = √3. Это значение имеет важное геометрическое значение и широко применяется в различных областях науки и техники.






