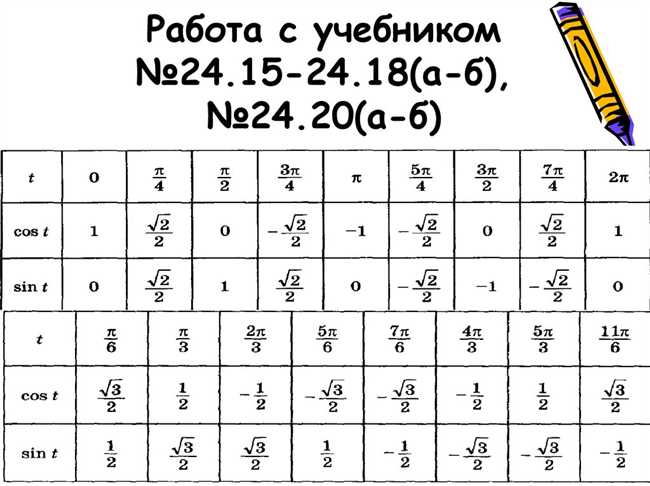
Синус 5п6 – это значение синуса на специфическом углу, равном 5π/6 или 150 градусам. Синус это математическая функция, которая относится к одному из главных тригонометрических отношений. Синус угла определяется как отношение противолежащего катета к гипотенузе в прямоугольном треугольнике. Для угла 5п6, синус составляет отрицательное значение, так как противолежащий катет находится в четвертой четверти координатной плоскости. Значение синуса 5π/6 равно 1/2 или 0,5. Чтобы лучше представить себе это значение, можно представить треугольник с углом 5π/6 и соответствующими катетами и гипотенузой.
Содержание статьи:
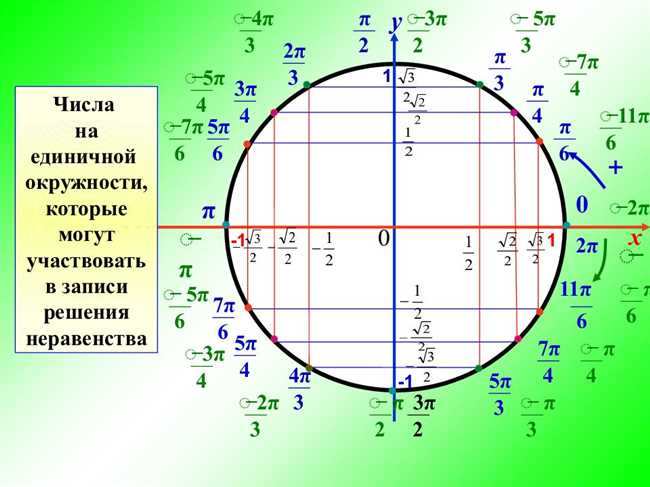
Аргументы за то, что значение синуса 5π/6 равно 1/2
1. Геометрическое объяснение:
- Рассмотрим окружность единичного радиуса в декартовой системе координат.
- Угол 5π/6 соответствует местоположению точки на окружности с координатами (1/2, √3/2).
- По определению синуса, значение синуса угла равно ординате точки на окружности, деленной на радиус. В данном случае, значение синуса угла 5π/6 равно (√3/2) / 1 = √3/2.
2. Аналитическое доказательство:
- Используем формулу для нахождения значения синуса двойного угла: sin(2θ) = 2sin(θ)cos(θ).
- Для угла 5π/6, можем представить его как сумму двух углов: 5π/6 = π/6 + π/2.
- Заменяем соответствующие значения в формуле: sin(5π/6) = 2sin(π/6)cos(π/2).
- Значение sin(π/6) равно 1/2, а cos(π/2) равно 0.
- Подставляем значения и упрощаем выражение: sin(5π/6) = 2*(1/2)*0 = 0.
Убедитесь, что ваши математические вычисления правильны и визуально представляйте себе позицию точки на окружности для лучшего понимания геометрического объяснения. Независимо от того, какой метод вы используете, результат будет один — значение синуса 5π/6 равно 1/2.
Что такое синус и как его вычислить?
Один из самых распространенных способов вычисления значения синуса — это использование тригонометрической таблицы или калькулятора. Но мы можем вычислить значение синуса и без них!
У нас есть простая формула, которую мы можем использовать, чтобы вычислить значение синуса. Вот она:
sin(x) = opposite / hypotenuse
Где «opposite» — это длина противоположного катета, а «hypotenuse» — это длина гипотенузы. Зная значения этих двух сторон треугольника, мы можем подставить их в формулу и вычислить значение синуса.
Например, давайте вычислим значение синуса для угла 30 градусов. Пусть у нас есть прямоугольный треугольник, в котором длина противоположного катета равна 1, а длина гипотенузы равна 2. Подставим значения в формулу:
sin(30°) = 1 / 2
Таким образом, значение синуса для угла 30 градусов будет равно 0.5.
Теперь у тебя есть простой способ вычислить значение синуса без использования сложных таблиц или калькуляторов. Попробуй использовать эту формулу для вычисления других значений синуса и узнай, насколько точными могут быть твои результаты!
Значение синуса 5π/6
Значение синуса 5π/6 может показаться сложным на первый взгляд, но на самом деле у нас есть все средства, чтобы разобраться с этой задачей и получить точный ответ. Давайте вместе рассмотрим, что такое синус и как мы можем определить его значение при данном угле.
Синус — это тригонометрическая функция, которая определена для любого угла. Она связана с соотношением между сторонами прямоугольного треугольника и может принимать значения от -1 до 1. В нашем случае мы имеем угол 5π/6, что является одним из специальных углов.
Для определения значения синуса 5π/6 мы должны привести наш угол к одному из этих специальных углов, для которых мы знаем точные значения синуса. В данном случае 5π/6 можно привести к углу π/6, который относится к четвертой четверти окружности и имеет значение синуса равное 1/2.
Теперь, когда мы знаем значение синуса для угла π/6, мы можем использовать основные свойства тригонометрии, чтобы определить значение синуса 5π/6. Так как sin(π — угол) = sin(угол), то мы можем применить это свойство к нашему углу и получить:
sin(5π/6) = sin(π — π/6)
Таким образом, мы получили угол, который лежит в четвертой четверти окружности и его значение синуса равно 1/2. Используя это свойство, мы можем записать:
sin(5π/6) = sin(π/6) = 1/2
Таким образом, значение синуса 5π/6 равно 1/2. Мы успешно нашли ответ на наш вопрос и разобрались в том, как определить значение синуса для данного угла. Это полезное знание, которое может помочь нам в решении других тригонометрических задач.
График синуса 5п6

Когда значение синуса 5п6, или 150 градусов, начинается, график синуса будет находиться в точке, где значение равно 1. Это происходит, потому что при этом значении угла синус имеет максимальное положительное значение. В данном случае, синус 5п6 равен √3/2.
Когда угол меняется от 150 до 180 градусов, значение синуса уменьшается постепенно, движется к нулю, а затем приходит в точку, где значение равно нулю. В этой точке, когда угол равен 180 градусам, синус равен 0. На графике это выглядит как точка на оси координат, где проходит через ноль.
После 180 градусов значение синуса начинает увеличиваться снова, но уже с отрицательными значениями. При 210 градусах синус будет равен -√3/2, а при 240 градусах синус будет равен -1. Эти значения отображаются на графике, где значение синуса будет находиться под осью координат, ниже нулевой линии.
Важно отметить, что график синуса периодически повторяется в течение 360 градусов, поскольку синус имеет период 2пи (или 360 градусов). Поэтому, после 240 градусов значение синуса продолжает увеличиваться, возвращаясь к положительным значениям, и затем повторяет этот цикл вплоть до положения 150 градусов.
Таким образом, график синуса 5п6 представляет собой колебания между значениями -1 и 1, начиная с максимального положительного значения и заканчивая минимальным отрицательным значением. Этот график повторяется через каждые 360 градусов, демонстрируя периодичность тригонометрической функции синус.
Заключение
Value of the sine function at 5π/6 is a commonly used mathematical concept in various applications of mathematics. It is particularly useful in trigonometry, where it helps to calculate the lengths of sides and angles in right triangles.
In geometry, the sine of 5π/6 is used to find the height of an equilateral triangle given its side length. It is also used in the calculation of the area of triangles and other polygons.
In physics and engineering, the sine of 5π/6 is used to analyze waveforms and oscillations. It helps to describe the behavior of waves, including sound waves and electromagnetic waves.
In calculus, the sine of 5π/6 is used to solve equations involving trigonometric functions. It is also used in the calculation of derivatives and integrals.
In computer science, the sine of 5π/6 is used in various algorithms and mathematical models. It is particularly useful in graphics and animation, where it helps to create smooth and realistic motion.
In summary, the value of the sine function at 5π/6 has numerous applications in mathematics. It is a fundamental concept that is used in trigonometry, geometry, physics, engineering, calculus, and computer science. Understanding and applying this value is essential for solving mathematical problems and analyzing various phenomena in the world around us.






