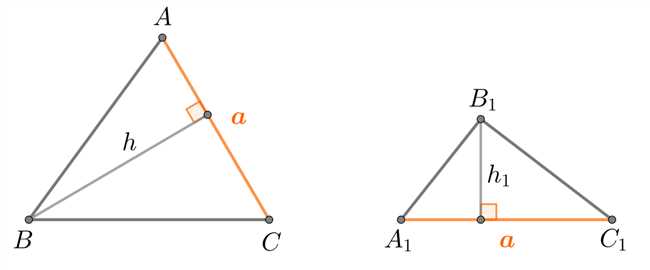
Высота треугольника является важным понятием в геометрии, которое определяет расстояние от вершины треугольника до противоположной стороны. Когда основание треугольника разбивается на два отрезка, например 8 и 9, существует несколько способов решения задачи нахождения высоты. Один из популярных методов — использовать подобные треугольники и пропорции. Другой метод заключается в применении формулы, основанной на площади треугольника и его основании. Каждый из этих способов позволяет получить точные значения высоты треугольника при заданных условиях.
Способы решения задачи о нахождении высоты треугольника
Существует несколько способов решения задачи о нахождении высоты треугольника, в зависимости от доступной информации о треугольнике.
Способ 1: Использование формулы площади треугольника
Один из наиболее распространенных способов решения задачи о высоте треугольника — использование формулы площади треугольника. Если известны длины сторон треугольника и необходимо найти высоту, можно воспользоваться следующей формулой:
Высота = 2 * Площадь / Длина основания
Где Площадь треугольника может быть найдена с помощью формулы Герона для треугольников с заданными сторонами.
Способ 2: Использование теоремы Пифагора
Если известны длины двух сторон треугольника, а третья сторона является гипотенузой прямоугольного треугольника, можно воспользоваться теоремой Пифагора для нахождения длины высоты.
Согласно теореме Пифагора, в прямоугольном треугольнике с катетами a и b и гипотенузой c, выполнено следующее равенство:
a^2 + b^2 = c^2
Таким образом, можно найти длину третьей стороны треугольника и использовать ее для расчета высоты с помощью формулы из способа 1.
Способ 3: Использование свойств перпендикуляра
Если известны углы треугольника и одна из сторон, можно воспользоваться свойством перпендикуляра и тригонометрическими функциями для нахождения высоты.
Предположим, что известна длина стороны a, а угол между этой стороной и основанием треугольника равен α. Тогда высоту можно найти по следующей формуле:
Высота = a * sin(α)
Эта формула основана на свойстве перпендикуляра — высота треугольника является противоположным катетом в прямоугольном треугольнике, где угол между основанием и высотой равен α.
Выбор способа решения задачи о нахождении высоты треугольника зависит от имеющихся данных о треугольнике и уровня математической подготовки. Важно уметь грамотно применять эти способы для решения конкретных задач.
Метод площадей
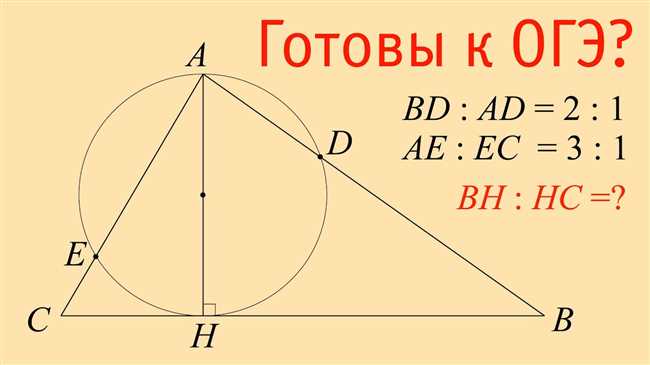
Как же работает метод площадей? Представьте, что у нас есть треугольник ABC с основанием AB, которое разбито точкой D на две отрезка AD и DB. Чтобы найти высоту треугольника, нам нужно найти площадь этого треугольника. Но нам неизвестна высота, поэтому мы разбиваем треугольник на два меньших треугольника: треугольник ADB и треугольник BDC.
Теперь мы можем вычислить площади этих двух треугольников. Площадь треугольника ADB равна половине произведения основания AD на высоту HD, а площадь треугольника BDC равна половине произведения основания BD на высоту HE. Заметьте, что высоты HD и HE — это искомая высота треугольника ABC.
Теперь, чтобы найти высоту треугольника ABC, мы просто складываем площади треугольников ADB и BDC и делим полученную сумму на длину основания AB:
Высота треугольника ABC = (площадь ADB + площадь BDC) / AB
Таким образом, метод площадей позволяет нам получить высоту треугольника, используя только известные длины основания и разбиение на два отрезка. Этот метод основан на принципе равенства площадей и не требует использования сложных тригонометрических выражений. Теперь вы можете легко вычислить высоту треугольника, даже если вам известны только длины основания и отрезков разбиения.
Метод подобия треугольников
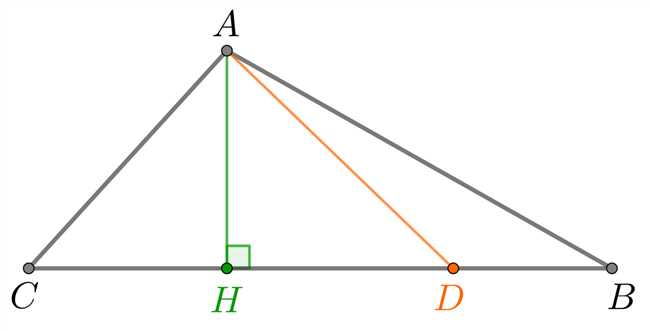
Для применения метода подобия треугольников необходимо знать, что два треугольника подобны, если их углы равны и соответствующие стороны пропорциональны. Таким образом, если мы разделим основание треугольника на два отрезка, то получим два подобных треугольника.
Давайте рассмотрим конкретный пример. Предположим, что основание треугольника равно 17 см, а мы разделили его на две части — 8 см и 9 см. Теперь нам нужно найти высоту треугольника.
Чтобы применить метод подобия треугольников, мы можем сравнить отношения сторон и высот в двух подобных треугольниках. Например, в нашем случае:
- В большем треугольнике, с основанием 17 см, соотношение сторон будет равно 17:8 = 2,125.
- В меньшем треугольнике, с основанием 8 см, соотношение сторон будет равно 8:9 = 0,889.
Мы можем использовать эти соотношения, чтобы найти высоту большего треугольника. Зная, что высота меньшего треугольника равна, например, 3 см, мы можем установить пропорцию:
2,125 / 0,889 = x / 3
Решая эту пропорцию, мы найдем высоту большего треугольника:
| 2,125 | 0,889 |
|---|---|
| x | 3 |
Найденное значение x будет равно высоте большего треугольника. С помощью этого метода можно найти высоту треугольника в любом случае разбиения основания на два отрезка.
Метод подобия треугольников является эффективным способом решения задачи о высоте треугольника при разбиении основания на два отрезка. Он позволяет использовать свойства подобия треугольников, чтобы найти высоту треугольника с помощью пропорций. Применяйте этот метод с уверенностью и достигайте успешных результатов!
Метод прямоугольных треугольников
Итак, давайте представим, что основание треугольника разбито на два отрезка: 8 и 9. Наша задача — найти высоту треугольника.
Для начала давайте построим прямоугольный треугольник, в котором одна из катетов будет равна одному из отрезков основания, а другой катет будет равен высоте треугольника. Давайте в качестве одного из катетов выберем отрезок основания, равный 8.
Теперь вспомним свойства прямоугольных треугольников. Один из них гласит, что произведение катетов прямоугольного треугольника равно произведению гипотенузы на высоту, опущенную на эту гипотенузу. Поэтому у нас есть соотношение: 8 * h = a * b, где h — искомая высота, а a и b — катеты прямоугольного треугольника. Заметим, что один из катетов равен 8, а гипотенуза будет равна сумме двух отрезков основания: 8 + 9 = 17.
Теперь мы знаем соотношение: 8 * h = 17 * b. Для решения этого уравнения нам нужно найти значение катета b. Мы можем найти его, используя теорему Пифагора: a^2 + b^2 = c^2. Подставим известные значения: 8^2 + b^2 = 17^2. Решив это уравнение, получим, что b^2 = 289 — 64 = 225. Извлекая квадратный корень, получим b = 15.
Теперь мы знаем значения двух катетов: a = 8 и b = 15. Подставим их в наше исходное соотношение: 8 * h = 17 * 15. Решив это уравнение, получим, что h = 1275 / 8 = 159,375.
Итак, ответ: высота треугольника, когда основание разбито на два отрезка 8 и 9, равна примерно 159,375 (с округлением до трех знаков после запятой).
Заключение
Используя эту теорему, мы можем определить высоту треугольника, если известны длины двух отрезков, на которые разбито его основание. Нам достаточно найти длину третьего отрезка, который является гипотенузой прямоугольного треугольника, образованного высотой и катетами — отрезками, на которые разбито основание. Затем мы можем воспользоваться теоремой Пифагора, чтобы найти высоту треугольника.
Таким образом, метод теоремы Пифагора предоставляет нам простой и надежный способ нахождения высоты треугольника при заданном разбиении основания на два отрезка. Он основан на фундаментальной теореме Пифагора и может быть применен в различных задачах, связанных с геометрией и треугольниками.






