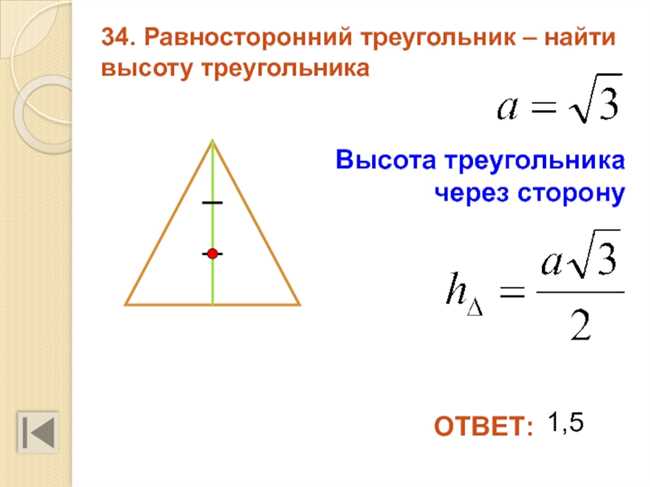
Все высоты равностороннего треугольника равны
Равносторонний треугольник является особым типом треугольника, у которого все стороны равны. Но, помимо равных сторон, равносторонний треугольник имеет еще одну интересную особенность — все его высоты равны.
Высоты треугольника — это перпендикуляры, опущенные из вершин треугольника на противоположные стороны. В случае равностороннего треугольника, все три высоты окажутся равными друг другу.
Это свойство может быть доказано геометрически, а также математически с использованием формул для расчета высот треугольника. Понимание данного свойства равностороннего треугольника позволяет упростить решение геометрических задач и улучшить понимание его структуры и свойств.
Определение равностороннего треугольника
Равносторонний треугольник, в свою очередь, является частным случаем равнобедренного треугольника, где все три стороны равны. Он отличается от равнобедренного треугольника тем, что у равностороннего треугольника все три угла также равны.
Этот тип треугольника имеет много интересных свойств и особенностей. Обрати внимание, что в равностороннем треугольнике также справедливы следующие утверждения:
- Все высоты равностороннего треугольника равны между собой.
- Биссектрисы углов равномерно делят противолежащие стороны.
- Медианы равностороннего треугольника также делятся равными отрезками.
- Центр описанной окружности равностороннего треугольника совпадает с центром равностороннего треугольника.
Равносторонний треугольник может быть использован в различных задачах и конструкциях. Например, он часто используется как основа для создания равносторонних многоугольников или как основной элемент в архитектуре и дизайне.
Так что теперь ты знаешь, что такое равносторонний треугольник. Обрати внимание на его равные стороны и углы, а также на свойства и особенности этого треугольника. Равносторонний треугольник — это не только простая геометрическая фигура, но и символ равенства и гармонии.
Свойства равностороннего треугольника
Свойство 1: Равные стороны
Главное свойство равностороннего треугольника – все его стороны равны между собой. Например, если одна сторона равна 5 см, то все остальные стороны также будут равны 5 см. Это делает треугольник симметричным и эстетически приятным для глаза.
Свойство 2: Равные углы
В равностороннем треугольнике все его углы равны между собой. Каждый из углов равен 60 градусам. Это значит, что треугольник имеет три равных угла и является равноугольным. Такой треугольник можно представить как ровный угол на три равные части.
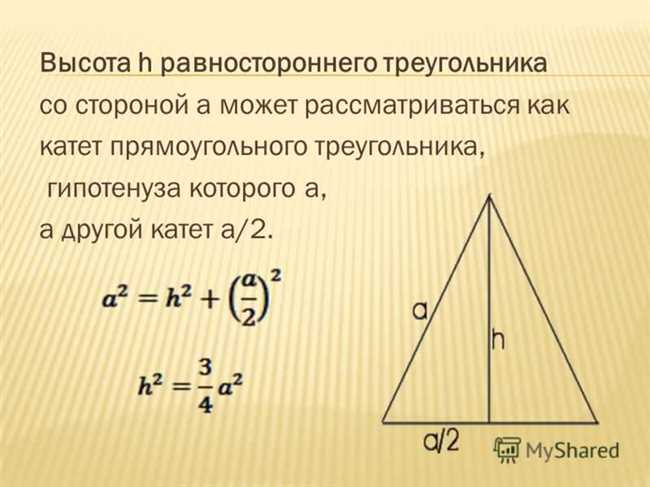
Свойство 3: Равные высоты
В равностороннем треугольнике все его высоты равны между собой. Высота треугольника – это отрезок, проведенный из вершины треугольника к основанию, перпендикулярно к основанию. Так как все стороны равны, то все высоты также будут равны. Это свойство делает равносторонний треугольник симметричным относительно своих высот.
Свойство 4: Формула для нахождения площади
Равносторонний треугольник имеет удобную формулу для нахождения его площади. Для этого нужно знать длину одной из его сторон. Площадь равностороннего треугольника можно вычислить по формуле: S = (a^2 * √3) / 4, где S – площадь треугольника, a – длина стороны.
Свойства равностороннего треугольника делают его интересным объектом для изучения и применения в различных областях науки и техники. Он является основой для конструирования геометрических фигур, а также используется в решении задач по тригонометрии и геометрии. Изучение свойств равностороннего треугольника помогает развивать логическое мышление, улучшать навыки решения геометрических задач и расширять общий кругозор.
Доказательство равенства высот равностороннего треугольника
Таким образом, высоты равностороннего треугольника сходятся в единой точке, которая является одновременно центром окружности, описанной вокруг треугольника. А значит, длины всех трех высот равны, так как радиус этой окружности одинаков для всех трех сторон треугольника. В свою очередь, равенство всех высот означает, что все три высоты представляют собой перпендикуляры, опущенные из вершин треугольника на прямые, содержащие соответствующие стороны.






