- Острые углы прямоугольного треугольника
- Прямоугольный треугольник и его свойства
- Соотношение углов в остроугольном треугольнике
- Углы 84 и 6 градусов
- Высота и медиана в прямоугольном треугольнике
- Высота треугольника
- Медиана треугольника
- Угол между высотой и медианой
- Угол между высотой и медианой в треугольнике

В прямоугольном треугольнике с острыми углами 84 и 6 градусов, угол между высотой и медианой является одним из интересных аспектов геометрии. Изучая углы и их свойства в данном треугольнике, можно понять, как они взаимодействуют и как это может влиять на структуру треугольника. Угол между высотой и медианой может быть как острый, так и тупой, и его величина зависит от конкретных значений углов прямоугольного треугольника. Понимание этого угла позволяет глубже погрузиться в изучение геометрии треугольников и их свойств.
Острые углы прямоугольного треугольника
Давайте рассмотрим прямоугольный треугольник с острыми углами 84 и 6 градусов. Один из острых углов равен 84 градусам, а другой — 6 градусам. При этом сумма этих углов составляет 90 градусов, что совпадает с определением прямоугольного треугольника.
В прямоугольном треугольнике высота и медиана являются важными сторонами и углами. Высота — это линия, которая проходит через вершину треугольника и перпендикулярна основанию. Она разделяет основание на две равные части и образует прямой угол со стороной основания. Медиана — это линия, которая соединяет любую вершину треугольника с серединой противоположной стороны.
В нашем случае, мы имеем прямоугольный треугольник со сторонами, образованными острыми углами 84 и 6 градусов. Медиана, проходящая через вершину с прямым углом и середину противоположной стороны, создает два острых угла. Угол между медианой и высотой будет равным сумме острых углов треугольника, то есть 84 + 6 = 90 градусов.
В итоге, угол между высотой и медианой в прямоугольном треугольнике с острыми углами 84 и 6 градусов будет равен 90 градусам.
Прямоугольный треугольник и его свойства
1. Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Это одно из самых известных свойств прямоугольных треугольников. Например, если у нас есть треугольник со сторонами 3 и 4, то гипотенуза будет равна 5, так как 3² + 4² = 9 + 16 = 25, и √25 = 5.
2. Соотношения между сторонами. В прямоугольном треугольнике стороны между собой взаимосвязаны следующим образом:
- Гипотенуза (самая длинная сторона) является противоположной стороной прямого угла.
- Катеты (две оставшиеся стороны) являются прилежащими сторонами прямого угла.
Это соотношение сторон позволяет нам вычислять длины сторон прямоугольного треугольника, если нам известны длины двух из них. Например, если у нас есть треугольник со сторонами 3 и 4, то длина гипотенузы будет 5.
3. Углы прямоугольного треугольника. В прямоугольном треугольнике сумма углов всегда равна 180 градусов. Это означает, что если один угол является прямым (90 градусов), то другие два угла в сумме будут равны 90 градусам.
Также в прямоугольном треугольнике существуют такие понятия, как высота и медиана:
- Высота – это отрезок, соединяющий вершину прямого угла с противоположной стороной. Она образует прямой угол с этой стороной и является показателем расстояния от вершины до этой стороны.
- Медиана – это отрезок, соединяющий середину одной из сторон прямоугольного треугольника с противоположной вершиной. В прямоугольном треугольнике, каждая медиана делит данный треугольник на равные по площади прямоугольники.
Интересно, что в прямоугольном треугольнике угол между высотой и медианой, проведенными из одной вершины, всегда равен 45 градусам. Это свойство может быть использовано для различных геометрических задач.
Соотношение углов в остроугольном треугольнике

Остроугольный треугольник, как следует из названия, имеет все три угла острые, то есть меньше 90 градусов. В таком треугольнике есть несколько интересных соотношений между его углами, которые помогают нам лучше понять его свойства и особенности.
Первое соотношение, которое стоит упомянуть, это то, что сумма углов остроугольного треугольника всегда равна 180 градусов. Это означает, что если мы сложим все углы треугольника, мы получим точно 180 градусов, независимо от их величины.
Также, в остроугольном треугольнике, наибольший угол всегда противоположен наибольшей стороне, а наименьший угол — наименьшей стороне. Это обусловлено тем, что прямая сторона треугольника является самой длинной и соответствующий ей угол является самым большим.
Более конкретно, в нашем треугольнике с острыми углами 84 и 6 градусов, можно отметить следующие соотношения:
- Угол в прямоугольном треугольнике, противолежащий гипотенузе, всегда составляет 90 градусов.
- Два острых угла в остроугольном треугольнике всегда в сумме дают 90 градусов.
- У каждого острого угла в остроугольном треугольнике обязательно есть своя противолежащая сторона, которая является наибольшей среди трех сторон.
- Сумма длин двух меньших сторон всегда больше длины наибольшей стороны.
Такие соотношения между углами и сторонами помогают нам лучше понять геометрические свойства и особенности остроугольных треугольников. Изучение их позволяет строить математические модели и применять их в практических задачах.
Углы 84 и 6 градусов

Сначала давайте рассмотрим угол 84 градуса. Этот угол является острым углом, так как он меньше прямого угла (равного 90 градусам). Он также относится к острой стороне прямоугольного треугольника, то есть к стороне, которая лежит напротив прямого угла.
Далее перейдем к углу 6 градусов. Этот угол также является острым и представляет собой маленький угол в треугольнике. Он также относится к острой стороне и лежит напротив двух других углов — 84 градуса и прямого угла.
Теперь давайте рассмотрим, как связаны эти два угла с прямоугольным треугольником в целом. Угол 84 градуса является углом между высотой и гипотенузой треугольника, а угол 6 градусов — углом между медианой и острой стороной треугольника, лежащей вне медианы.
А теперь давайте взглянем на таблицу, которая показывает отношение длины высоты к длине медианы в прямоугольном треугольнике с углами 84 и 6 градусов:
| Угол | Высота | Медиана | Отношение |
|---|---|---|---|
| 84 градуса | h1 | m1 | h1/m1 |
| 6 градусов | h2 | m2 | h2/m2 |
В данной таблице h1, m1, h2 и m2 обозначают длины высоты и медианы для соответствующих углов 84 и 6 градусов.
Изучение этих значений поможет нам лучше понять взаимосвязь угла между высотой и гипотенузой с углом между медианой и острой стороной в прямоугольном треугольнике. Возможно, вы сможете найти интересные закономерности и связи, которые помогут вам в дальнейших геометрических и тригонометрических исследованиях.
Высота и медиана в прямоугольном треугольнике
В прямоугольном треугольнике, где острые углы составляют 84 и 6 градусов, можно рассмотреть высоту и медиану, которые имеют определенный угол между собой. Давайте разберемся, что это за линии и как они связаны.
Высота треугольника
Высота треугольника – это перпендикуляр, опущенный из вершины треугольника на основание или продолжение основания. В прямоугольном треугольнике, высота рассекает его на две равные части – это основание и другая сторона, образующая прямой угол с основанием. Угол между высотой и основанием в прямоугольном треугольнике всегда будет 90 градусов.
Чтобы найти высоту в прямоугольном треугольнике, можно воспользоваться теоремой Пифагора. Если основание треугольника – это сторона, которая является основанием прямого угла, а вторая сторона – это высота, то третья сторона будет гипотенузой прямоугольного треугольника. Таким образом, высоту можно найти по формуле h^2 = a^2 + b^2, где h – высота, а a и b – катеты прямоугольного треугольника.
Медиана треугольника
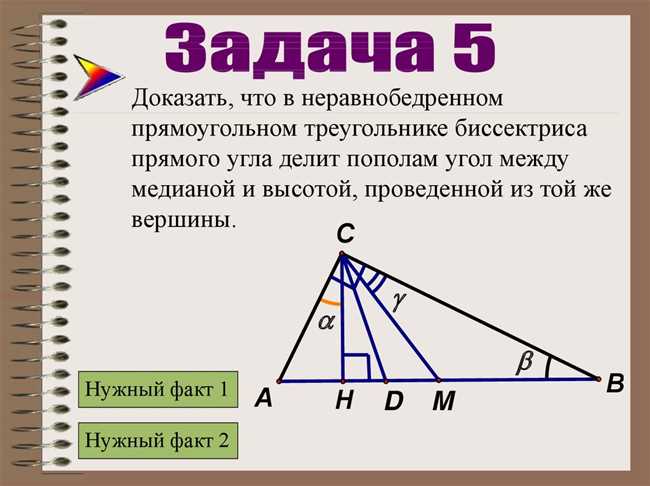
Медиана треугольника – это линия, которая соединяет вершину треугольника с серединой основания или продолжение основания. В прямоугольном треугольнике, медиана также рассекает его на две равные части. Угол между медианой и основанием может быть разным и зависит от углов треугольника.
Чтобы найти медиану в прямоугольном треугольнике, нужно учитывать, что медиана, проведенная из вершины прямого угла, будет равна половине гипотенузы. Если обозначить гипотенузу как c, то медиана будет равна c/2.
Угол между высотой и медианой
Угол между высотой и медианой в прямоугольном треугольнике может быть разным, в зависимости от углов треугольника. В данном случае, когда острые углы треугольника составляют 84 и 6 градусов, это означает, что острый угол между высотой и медианой будет равен 84 градусам.
Такой угол между высотой и медианой, равный 84 градусам, может иметь различные геометрические интерпретации и использоваться в различных задачах. Например, он может помочь в измерении расстояний или определении площади треугольника.
Важно помнить, что для каждого прямоугольного треугольника угол между высотой и медианой будет разным, и его значение зависит от углов треугольника. Таким образом, высота и медиана – важные элементы прямоугольного треугольника, которые имеют свои уникальные свойства и помогают в изучении его геометрии.
Угол между высотой и медианой в треугольнике
В прямоугольном треугольнике с острыми углами 84 и 6 градусов, угол между высотой и медианой также имеет определенное значение. Он равен 90 градусов, то есть высота и медиана перпендикулярны друг другу.
Это свойство обусловлено особенностями прямоугольного треугольника, где одна из сторон является высотой, проведенной из прямого угла, а другая сторона является медианой, проходящей через середину противоположной стороны.
Из этого следует, что угол между высотой и медианой в прямоугольном треугольнике всегда равен 90 градусам. Это важное свойство треугольника, которое может быть использовано в вычислительной геометрии или при решении задач по геометрии и тригонометрии.






