
Теорема о угле в 30 градусов и катет напротив – это важное математическое утверждение, которое может использоваться в различных сферах. Когда угол равен 30 градусам, соответствующий катет всегда равен половине гипотенузы. Это отношение используется в треугольнике 30-60-90, где один из углов равен 30 градусам. Утверждение также находит применение в естественных науках, особенно в физике. Например, при расчете силы, направления движения объекта или определении составляющих векторов. Теорема об угле в 30 градусов и катете противоположен подробно изучается в школьных учебниках математики и физики, и ее понимание позволяет более точно решать задачи и проводить анализ.
Теорема про угол в 30 градусов и катет напротив
В мире геометрии существует множество интересных и полезных теорем, одна из которых связана с углом в 30 градусов и катетом, который лежит напротив этого угла. Но что же такое эта теорема и как она может нам помочь в решении геометрических задач?
В общем, теорема гласит: если в треугольнике угол равен 30 градусам, то катет, лежащий напротив этого угла, равен половине гипотенузы. Необходимое условие для применения этой теоремы – наличие угла величиной 30 градусов в треугольнике.
Мы часто сталкиваемся с треугольниками в повседневной жизни. Например, если ты строишь дом садовыми инструментами, то ты, возможно, сталкиваешься с задачами, связанными с определением размеров или углов треугольников. В таких ситуациях знание теоремы про угол в 30 градусов и катет напротив может оказаться очень полезным.
Как применить эту теорему на практике? Представь, ты строишь перголу в своем саду и хочешь убедиться, что рама будет иметь угол в 30 градусов. Ты можешь измерить одну из боковых сторон рамы и разделить это значение на половину, чтобы определить длину катета, лежащего напротив угла в 30 градусов.
Но может возникнуть вопрос: «Как же мне измерить угол в 30 градусов?» Вот несколько способов, которые помогут тебе справиться с этой задачей:
- Использование геометрического инструмента, такого как транспортир. Он позволяет точно измерить угол.
- Создание равнобедренного треугольника с помощью линейки и компаса. Если два угла в этом треугольнике равны, то третий угол будет составлять 180 — 2*30 = 120 градусов.
- Использование готовых геометрических фигур, которые имеют угол в 30 градусов, например, специального угольника.
Теорема про угол в 30 градусов и катет напротив важна не только для решения задач в геометрии, но и для развития нашего логического мышления и умения анализировать информацию. Она показывает нам, что математика применима не только в классе, но и в повседневной жизни.
Объяснение теоремы
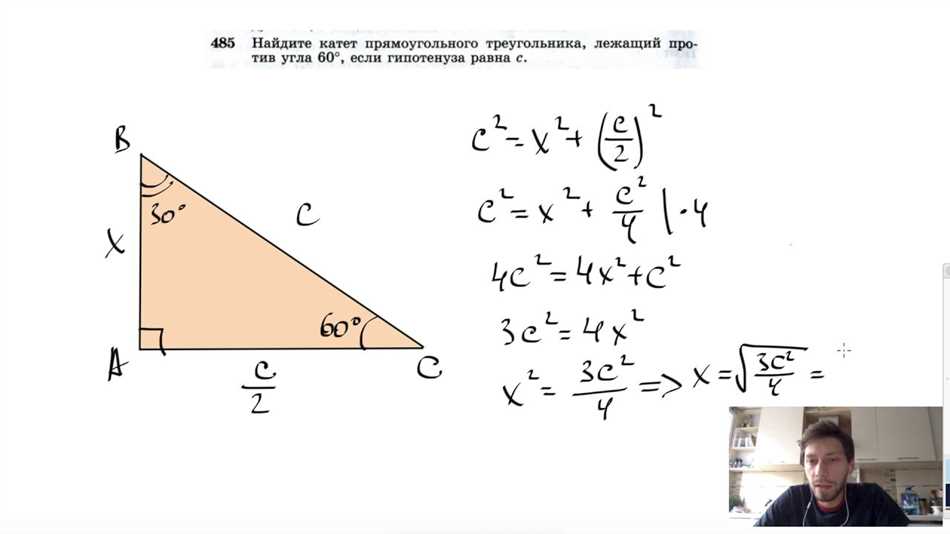
Представь себе ситуацию: ты решил построить прямоугольный треугольник и наткнулся на проблему. Как найти длину катета, если известен только угол в 30 градусов? Теорема про угол в 30 градусов и катет напротив приходит на помощь!
Перед тем, как погрузиться в объяснение теоремы, давай разберемся с основами. Что такое угол и катет? Угол — это величина, измеряющая поворот или наклон между двумя лучами или отрезками. Самый простой способ представить угол — это полукруг, где центр — точка схода лучей (вершина угла), а лучи — отрезки, исходящие из этой точки. Катет — это один из двух отрезков, составляющих прямоугольный треугольник, лежащий при основании или вблизи его.
Теперь перейдем к теореме про угол в 30 градусов и катет напротив. Главная идея заключается в следующем: если в прямоугольном треугольнике один из углов равен 30 градусам, то длина катета напротив этого угла будет равна половине гипотенузы, то есть самого длинного отрезка треугольника.
Но как это работает? Давай рассмотрим пример. Представь себе прямоугольный треугольник с углом в 30 градусов. В этом треугольнике существуют три стороны: гипотенуза, которая находится напротив прямого угла, и два катета, которые образуют острые углы.
| h | a | b |
|---|---|---|
| Гипотенуза | a | b |
| 30° |
Предположим, что длина гипотенузы равна 10 единицам. Согласно теореме, катет напротив угла в 30 градусов будет равен половине гипотенузы, то есть 5 единицам. Это можно объяснить следующим образом: если угол в 30 градусов занимает только 1/3 от всего круга (360 градусов), то катет, лежащий напротив него, занимает такую же долю от гипотенузы.
Теперь представь, что ты знаешь длину катета, но не знаешь длину гипотенузы. Используя теорему про угол в 30 градусов и катет напротив, ты можешь найти гипотенузу. Давай решим такую задачу: катет напротив угла в 30 градусов равен 7 единицам. Какая будет длина гипотенузы?
Так как катет напротив угла в 30 градусов равен половине гипотенузы, мы можем записать уравнение: 7 = 1/2 * гипотенуза. Чтобы найти значение гипотенузы, мы умножим 7 на 2, получив 14 единиц.
Теорема про угол в 30 градусов и катет напротив очень полезна в геометрии и в решении различных задач, связанных с треугольниками. Умение применять эту теорему поможет тебе не только в школе, но и в повседневной жизни. Например, можно использовать ее для измерения расстояния до объектов, когда известен угол обзора.
Так что не бойся углов в 30 градусов и находи катеты напротив смело! Теорема стоит на страже точных измерений и геометрических рассуждений.
Доказательство теоремы про угол в 30 градусов и катет напротив
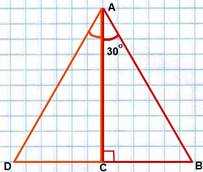
Во-первых, давайте рассмотрим треугольник ABC, в котором угол BAC равен 30 градусам. Нам нужно доказать, что отрезок BC (катет) равен половине отрезка AB (гипотенуза).
Для доказательства этой теоремы мы воспользуемся свойствами треугольника и тригонометрией. Рассмотрим треугольник ABC.
1. Найдем высоту треугольника, опущенную из вершины A на сторону BC. Обозначим ее точкой D.
2. Поскольку угол BAC равен 30 градусам, угол DBA равен 60 градусам (сумма углов треугольника равна 180 градусам).
3. Также у нас есть соотношение между сторонами и углами треугольника, известное как тригонометрический закон или закон синусов. Он гласит, что отношение длины стороны к синусу противолежащего ей угла одинаково для всех сторон треугольника.
4. Применив закон синусов к треугольнику ABC, мы получаем следующее равенство: BC / sin(60) = AB / sin(30).
5. Поскольку sin(60) = √3/2 и sin(30) = 1/2, у нас получается следующее равенство: BC / (√3/2) = AB / (1/2).
6. Упростив это равенство, мы получаем следующее: BC = AB * √3.
7. Таким образом, мы доказали, что катет BC равен гипотенузе AB, умноженной на √3.
Теперь, когда у нас есть доказательство этой теоремы, давайте посмотрим, как она может быть применена в реальной жизни.
Например, представьте себе, что у вас есть треугольник ABC, в котором угол BAC равен 30 градусам, а длина гипотенузы AB равна 10 сантиметрам.
Используя теорему про угол в 30 градусов, мы можем вычислить длину катета BC. Подставив значения в формулу BC = AB * √3, мы получим BC = 10 * √3 ≈ 17,32 сантиметра.
Таким образом, доказательство этой теоремы позволяет нам вычислять длины сторон треугольника, если известен угол BAC и длина гипотенузы.
Заключение
В данной статье были рассмотрены несколько примеров применения этой теоремы. Мы узнали, как использовать ее для нахождения длины катета напротив угла в 30 градусов и для вычисления площади прямоугольного треугольника.
Также мы рассмотрели применение теоремы в реальных ситуациях. Например, она может быть использована в строительстве для определения уровня наклона крыши или в авиации для расчета траектории полета самолета.
Таким образом, теорема про угол в 30 градусов и катет напротив является полезным инструментом в геометрии, который может иметь широкий спектр применения в различных областях. Понимание и использование этой теоремы поможет нам лучше понять и работать с геометрическими объектами, а также применять их в практических задачах.






