Когда решаем задачи по геометрии, нам часто требуется найти тангенс угла. Тангенс — это отношение противоположной стороны к прилежащей стороне треугольника. Если изначально у вас нет таблицы тангенсов или калькулятора под рукой, вы можете использовать клеточки для нахождения этого значения. Этот метод особенно полезен для работы с прямоугольными треугольниками и построения графиков функций. Найти тангенс угла с использованием клеточек несложно, нужно только знать несколько простых правил и следовать им при выполнении вычислений. В этом подробном руководстве мы рассмотрим, как найти тангенс угла с помощью клеточек и приведем примеры для лучшего понимания.
Руководство: как найти тангенс угла через клеточки
Давайте представим, что перед вами есть прямоугольная сетка, разделенная на клеточки. Мы будем использовать эту сетку для определения тангенса угла. Нашей целью является нахождение отношения длины противоположного катета к длине прилежащего катета.
Для начала, выберите угол, для которого вы хотите найти тангенс. Проведите линию через этот угол так, чтобы она проходила через начало координат и пересекала сетку. Отметьте точку на этой линии, где она пересекает противоположный катет, и точку, где она пересекает прилежащий катет.
Теперь посчитайте количество клеточек по горизонтали и вертикали между этими двумя точками. Обозначим количество клеточек по горизонтали как «a» и по вертикали как «b». Затем найдите отношение «a» к «b».
Вот и все! Это отношение является тангенсом угла, который вы выбрали. Тангенс угла равен противоположному катету (вертикальной стороне треугольника) деленному на прилежащий катет (горизонтальную сторону треугольника).
К примеру, если вы нашли отношение «a» к «b» равное 2/3, то тангенс этого угла будет 2/3.
Теперь вы знаете, как найти тангенс угла с помощью клеточек! Этот метод очень прост и удобен, и он может быть полезен при решении различных задач в геометрии и физике. Надеюсь, что эта информация окажется вам полезной и поможет вам в вашей учебе и работе. Удачи!
Раздел 2: Понятие тангенса угла
Тангенс угла определяется как отношение противоположной стороны к прилежащей стороне прямоугольного треугольника. Прежде чем мы более подробно рассмотрим это определение, вспомним, что такое прямоугольный треугольник.
- Прямоугольный треугольник — это треугольник, у которого один из углов равен 90 градусам.
Теперь вернемся к тангенсу угла. Вот формула, которая позволяет нам вычислить тангенс:
тангенс угла = противоположная сторона / прилежащая сторона
Эта формула основана на теореме Пифагора, которая утверждает, что сумма квадратов катетов равна квадрату гипотенузы в прямоугольном треугольнике.
Теперь, когда мы знаем формулу, давайте рассмотрим некоторые примеры использования тангенса угла. Предположим, у нас есть прямоугольный треугольник с углом 30 градусов и сторонами 3 и 4.
- Противоположная сторона для угла 30 градусов равна 3.
- Прилежащая сторона для угла 30 градусов равна 4.
Теперь мы можем использовать формулу тангенса, чтобы найти значение:
тангенс 30 градусов = 3 / 4 ≈ 0.75
Итак, тангенс угла 30 градусов составляет примерно 0.75.
Как видите, тангенс угла может быть полезным инструментом для вычислений и измерений в геометрии. Он позволяет нам определить отношение между двумя сторонами прямоугольного треугольника и, соответственно, углом.
Теперь, когда вы знакомы с понятием тангенса угла, вы можете использовать его для решения различных геометрических задач и измерений. Учитесь и практикуйтесь с вычислениями, и используйте тангенс в своей работе!
Раздел 3: Метод нахождения тангенса через клеточки
Чтобы приступить к использованию этого метода, первым делом необходимо изобразить треугольник на клетчатой бумаге или на экране компьютера. Каждая сторона треугольника будет представлена в виде линии, проходящей через вершины клеток.
Важно помнить, что для нахождения тангенса нам необходимо знать значения двух сторон треугольника. Обычно эти значения известны, например, в задаче или упражнении даны численные данные о длинах сторон. Если таких данных нет, то мы можем сами придумать числа и обыграть ситуацию.
Следующим шагом я предлагаю наметить горизонтальную и вертикальную оси на решетке клеток. Это поможет нам определить смещение и длину сторон треугольника. Не забудь указать масштаб. Теперь можем приступить к нахождению тангенса угла.
Для начала, найдем значение тангенса угла через соотношение сторон треугольника. Вспомни, что тангенс равен отношению противоположной стороны к прилежащей стороне:
тангенс угла = противоположная сторона / прилежащая сторона
Теперь, используя значения сторон треугольника, которые мы определили на клеточной бумаге или на экране компьютера, подставим их в формулу и получим значение тангенса угла.
Обрати внимание, что тангенс может быть как положительным, так и отрицательным, в зависимости от положения угла относительно осей координат.
Поздравляю! Теперь ты знаешь еще один способ нахождения тангенса угла, и можешь применять его в упражнениях и решении геометрических задач. Удачи!
Раздел 4: Примеры применения метода
В данном разделе мы рассмотрели несколько примеров применения метода нахождения тангенса угла через клеточки. Приведенные ниже примеры помогут вам лучше понять, как использовать данный метод в практических задачах.
Пример 1: Вычисление тангенса угла прямоугольного треугольника
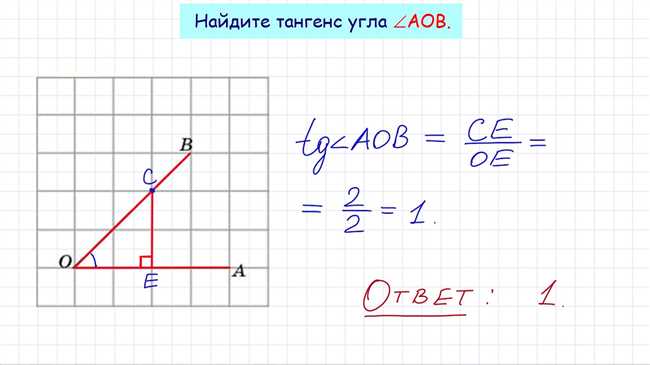
Рассмотрим пример прямоугольного треугольника, у которого известны значения двух катетов. Для нахождения тангенса угла α, нужно поделить длину противоположенного катета на длину прилежащего катета.
Пример:
- Длина прилежащего катета a = 3 клетки
- Длина противоположенного катета b = 4 клетки
Таким образом, тангенс угла α будет равен b/a = 4/3.
Пример 2: Нахождение тангенса угла в прямоугольной системе координат
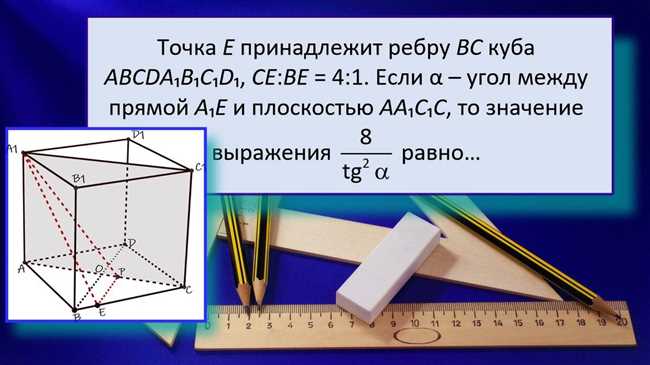
В прямоугольной системе координат угол может быть задан координатами точки на плоскости. Для нахождения тангенса такого угла нужно найти отношение координаты y к координате x.
Пример:
- Координата x = -2 клетки
- Координата y = 5 клеток
Тангенс такого угла будет равен y/x = 5/(-2).






