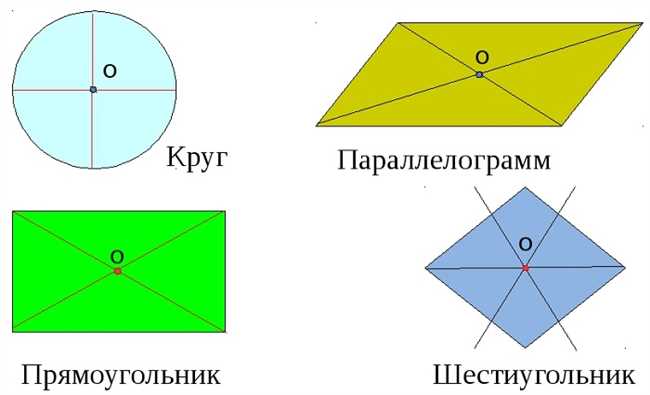
Геометрические фигуры с центральной и осевой симметрией являются одними из основных объектов изучения в геометрии. Центральная и осевая симметрии играют важную роль в определении симметричных и упорядоченных форм. Центральная симметрия обусловлена наличием оси вращения, вокруг которой фигура вращается таким образом, что она выглядит одинаково в любой позиции. Осевая симметрия, с другой стороны, происходит вдоль одной оси, где половина фигуры является зеркальным отображением другой половины. Некоторые примеры геометрических фигур с центральной симметрией включают круг, эллипс и шестиугольник, а с осевой симметрией — квадрат, прямоугольник и треугольник. Понимание этих симметричных шаблонов помогает нам визуально оценивать и классифицировать различные формы в окружающем нас мире.
Геометрические фигуры с центральной симметрией
1. Круг: Круг является одной из основных геометрических фигур с центральной симметрией. Любая точка на окружности равноудалена от центра, что делает его идеальным примером фигуры с центральной симметрией.
2. Эллипс: Эллипс также обладает центральной симметрией. Все точки на эллипсе имеют парные равноудаленные точки от центра, что создает симметричное отображение.
3. Равнобедренный треугольник: Равнобедренный треугольник имеет ось симметрии, проходящую через его вершину и середину основания. Фигура может быть разделена на две равные половины, симметрично отражающие друг друга.
4. Прямоугольник: Прямоугольник также является фигурой с центральной симметрией. Линия симметрии проходит через его центр и разделяет его на две равные половины.
5. Квадрат: Квадрат обладает центральной симметрией. Все его стороны и углы равны, а линия симметрии проходит через его центр.
6. Ромб: Ромб также обладает центральной симметрией. Все его стороны равны, а линия симметрии проходит через его центр и разделяет ромб на две равные части.
7. Восьмиугольник: Восьмиугольник имеет центр симметрии, который делит его на две равные половины. Линия симметрии проходит через центр восьмиугольника.
8. Круглый треугольник: Круглый треугольник имеет центр симметрии, лежащий на его высоте. Все точки треугольника равноудалены от центра, что создает симметрию.
9. Круглый прямоугольник: Круглый прямоугольник также обладает центральной симметрией. Все его стороны равны и линия симметрии проходит через его центр.
Это лишь несколько примеров геометрических фигур с центральной симметрией. Зная эти фигуры, вы сможете легко обнаружить центральную симметрию в других фигурах и использовать ее для создания гармоничных и сбалансированных композиций.
Круг и его симметрия

Основное свойство круга — его центральная симметрия. Центральная симметрия означает, что любая прямая линия, проходящая через центр круга, разделит его на две половины, которые будут симметричны друг другу. Например, если мы проведем прямую линию через центр круга и отразим половину круга относительно центральной линии, мы получим симметричный круг.
Еще одно интересное свойство круга — его отражательная симметрия. Отражательная симметрия означает, что каждая точка на поверхности круга находится на равном расстоянии от его центра. Это означает, что если мы проведем прямую линию от центра круга до любой точки на его поверхности, а затем продолжим эту линию через центр, она также пересечет поверхность круга в другой точке, находящейся на том же расстоянии от центра, что и исходная точка. Таким образом, у круга есть бесконечное количество осей отражательной симметрии.
Стоит отметить, что симметрия круга делает его не только привлекательным, но также практичным и полезным в ряде областей, включая архитектуру, дизайн и математику. Например, в архитектуре круг используется для создания куполов и центральных фигур, которые придают зданиям величественность и гармонию. В дизайне круг часто используется для создания органичных и сочных форм, которые придают продуктам привлекательность. В математике круг — это одно из первых изучаемых фигур, и его свойства образуют основу для изучения геометрии и тригонометрии.
- Центральная симметрия — каждая прямая линия, проходящая через центр круга, делит его на две симметричные половины.
- Отражательная симметрия — каждая точка на поверхности круга находится на равном расстоянии от его центра.
- Симметрия делает круг привлекательным, практичным и полезным в разных областях.
Эллипс и его симметрия
Симметрия это свойство, при котором фигура выглядит идентично при определенных преобразованиях. В случае с эллипсом, у него есть два вида симметрии — центральная и осевая.
Центральная симметрия:
Центральная симметрия означает, что фигура выглядит идентично, если провести прямую линию через ее центр и отразить ее относительно этой линии. В случае с эллипсом, его центральной симметрией является то, что если разделить эллипс на две части соответствующие ранее описанному условию, то они будут полностью совпадать. Другими словами, если копировать и переворачивать одну половину эллипса, она будет идеально вписываться в другую половину.
Осевая симметрия:
Осевая симметрия означает, что фигура выглядит идентично при отражении относительно некоторой прямой линии, называемой осью симметрии. В случае с эллипсом, его осевой симметрией является то, что если провести прямую линию через его центр, то каждая точка эллипса будет симметрична относительно этой оси. Это означает, что если мы проведем отрезок от центра эллипса до его периферии, а затем продолжим его на такое же расстояние в противоположную сторону, мы также получим точку эллипса.
Треугольник и его симметрия
Одной из особенностей треугольника является симметрия. Симметрия — это качество, при котором фигура может быть перевернута, повернута или отражена в отношении оси или точки, при этом сохраняя свою форму. Треугольник может иметь два вида симметрии — центральную и осевую.
Центральная симметрия треугольника означает, что треугольник можно разделить на две равные части, путем проведения линии от одной вершины через центр треугольника до противоположной вершины. Таким образом, форма и размеры треугольника будут зеркально отражены относительно центральной линии. Это создает гармоничный и симметричный образ.
Осевая симметрия треугольника возникает, когда существует ось, которая разделяет треугольник на две равные части. Ось симметрии проходит через середину одной стороны и перпендикулярна этой стороне. Таким образом, одна половина треугольника является зеркальным отражением другой половины относительно оси. Осевая симметрия создает ощущение равновесия и гармонии.
- Центральная симметрия:
- Проведение линии от одной вершины через центр треугольника до противоположной вершины;
- В результате форма и размеры треугольника зеркально отражены относительно центральной линии.
- Осевая симметрия:
- Существует ось, которая разделяет треугольник на две равные части;
- Ось симметрии проходит через середину одной стороны и перпендикулярна этой стороне;
- Одна половина треугольника является зеркальным отражением другой половины относительно оси.
Симметрия является важной особенностью треугольника и добавляет ему красоту и эстетическое качество. Она также используется в различных областях науки и искусства, включая архитектуру, живопись и дизайн. Благодаря симметрии треугольник может быть использован в создании уникальных и гармоничных композиций.
Запомните, треугольник — это не только простая геометрическая фигура, но и фигура с симметрией, которая делает его особенным и привлекательным. Попробуйте рассмотреть треугольники вокруг вас и обратите внимание на их симметрию. Наслаждайтесь их красотой и вдохновляйтесь!
Раздел 2: Геометрические фигуры с осевой симметрией
Прямоугольник
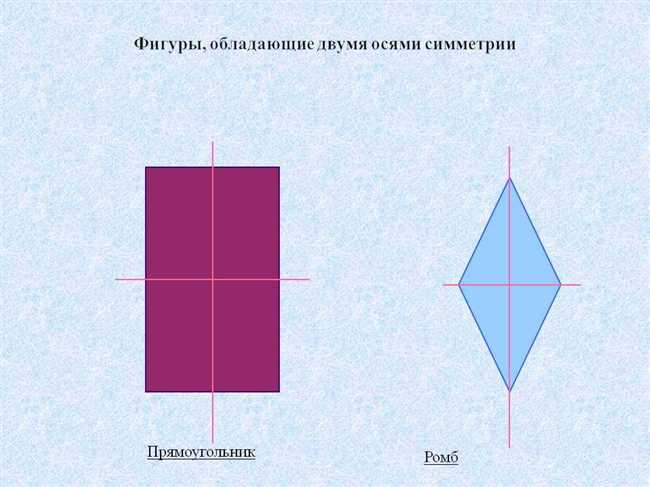
Прямоугольник является одной из наиболее распространенных фигур с осевой симметрией. Он обладает двумя осевыми симметричными линиями — горизонтальной и вертикальной. При вращении прямоугольника на 180 градусов вокруг этих линий, он остается неизменным. Таким образом, прямоугольник имеет две оси симметрии.
Квадрат
Квадрат также является фигурой с осевой симметрией. У квадрата есть 4 оси симметрии — две горизонтальные и две вертикальные. При вращении на 180 градусов вокруг любой из этих осей, квадрат остается неизменным.
Круг
Круг — это фигура с бесконечным количеством осей симметрии. Любая линия, проходящая через центр круга, является осью симметрии. При повороте на 180 градусов вокруг любой из этих осей, круг сохраняет свою форму.
Эллипс
Эллипс также обладает осевой симметрией. У него есть две оси симметрии — большая ось и малая ось, которые проходят через его центр. При вращении на 180 градусов вокруг этих осей, эллипс остается неизменным.
Треугольник
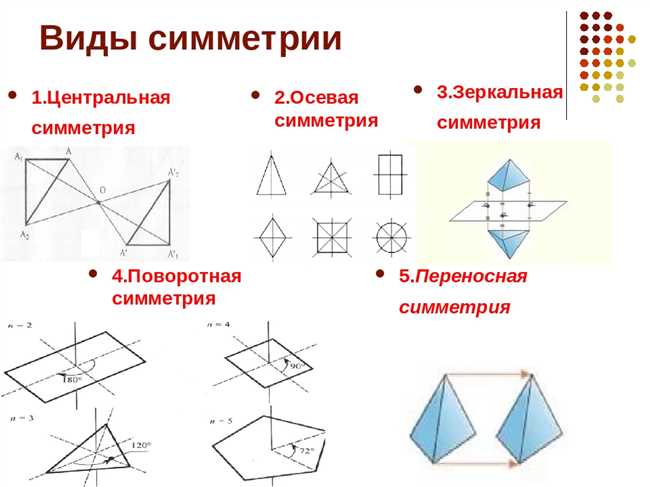
Некоторые треугольники также могут обладать осевой симметрией. Они называются равнобедренными треугольниками. Равнобедренный треугольник имеет одну ось симметрии — линию биссектрисы угла. При вращении на 180 градусов вокруг этой оси, равнобедренный треугольник сохраняет свою форму.
Осевая симметрия — это важный аспект геометрии, который помогает нам анализировать и понимать формы и фигуры. Она используется в различных областях, включая архитектуру, дизайн и искусство. Понимание осевой симметрии поможет вам в креативных проектах и в создании гармоничных и сбалансированных композиций.
Заключение
Осевая симметрия квадрата означает, что он можно разделить пополам по одной из его диагоналей или по одной из его осей симметрии. Это означает, что если мы сложим квадрат по этой линии, его две половинки будут идеально совпадать. Такая симметрия делает квадрат сбалансированным и гармоничным.
Центральная симметрия квадрата означает, что его можно разделить на две симметричные части относительно его центра. В этом случае, если мы сложим квадрат вдвое, его две половинки также будут идеально совпадать. Эта симметрия придает квадрату уникальность и эстетическую привлекательность.
Таким образом, квадрат — это не только простая геометрическая фигура, но и объект, обладающий удивительной симметрией. Она делает его не только полезным для различных задач в математике и физике, но и красивым визуально. Изучение симметрии квадрата не только помогает понять его структуру и свойства, но и открывает возможности для творческой интерпретации и использования в искусстве и дизайне.






