- Ограничения на составление трехзначных чисел
- Для трехзначного числа требуется отсутствие цифр 0, 3 и 7
- Расчет количества возможных трехзначных чисел
- Определение количества цифр, которых нужно избежать
- Расчет количества возможных цифр для каждой позиции числа
- Пример расчета количества трехзначных чисел без цифр 0, 3 и 7
- Вычисление количества трехзначных чисел без цифр 0, 3 и 7

Считайте десятичные числа, в которых могут быть любые цифры, кроме 0, 3 и 7. В каждом из трех разрядов имеется 7 цифр, поэтому общее число трехзначных чисел равно 7 * 7 * 7 = 343. Однако нам нужно исключить числа, в которых присутствует 0, 3 или 7. Из первых двух разрядов мы можем выбрать 6 цифр (то есть исключить 1, 3 или 7), а из третьего разряда — все 7. Таким образом, мы исключаем 6 * 6 * 7 = 252 числа. Окончательное количество трехзначных чисел без цифр 0, 3 и 7 равно 343 — 252 = 91.
Ограничения на составление трехзначных чисел
Но насколько эти ограничения влияют на возможность составления трехзначных чисел? Давайте посмотрим на некоторые детали.
Влияние отсутствия цифры 0:
У нас есть девять цифр (1, 2, 3, 4, 5, 6, 7, 8, 9), из которых мы можем выбирать для каждой позиции в трехзначном числе. Казалось бы, отсутствие нуля не должно иметь большого значения, верно? Однако на самом деле, отсутствие нуля означает, что у нас нет возможности создавать трехзначные числа, в которых одна или две позиции заняты нулем. Таким образом, мы теряем некоторые числа, которые могли бы быть составлены.
Влияние отсутствия цифры 3:
По аналогии с отсутствием цифры 0, отсутствие цифры 3 заметно снижает количество трехзначных чисел, которые мы можем составить. Вновь у нас остается восемь возможных цифр (1, 2, 4, 5, 6, 7, 8, 9), но на этот раз нам не разрешено использовать 3 в качестве цифры на любой позиции. Это означает, что мы теряем еще больше чисел, которые могли бы быть составлены.
Влияние отсутствия цифры 7:
Наконец, отсутствие цифры 7 также оказывает свое влияние на составление трехзначных чисел. Опять же, у нас остается восемь возможных цифр (1, 2, 3, 4, 5, 6, 8, 9), но мы не можем использовать 7 на любой позиции. И это означает, что еще больше чисел становятся недоступными для нас.
Как всегда, когда мы имеем ограничения, нам приходится выбирать из меньшего количества вариантов. В данном случае, отсутствие цифр 0, 3 и 7 существенно сужает нашу возможность составить трехзначные числа. Однако это не значит, что нам не удастся составить ни одно трехзначное число без этих цифр. У нас все еще есть достаточно цифр, чтобы создавать числа.
Для трехзначного числа требуется отсутствие цифр 0, 3 и 7
Чтобы убедиться в этом, давай вспомним, какие числа можно получить, используя только цифры от 1 до 9. Очевидно, что первая цифра может быть любой из девяти доступных: 1, 2, 4, 5, 6, 8, 9. Это дает нам семь вариантов для первой цифры. Остальные две цифры также могут быть любыми из оставшихся восьми. А это значит, что для второй цифры у нас есть восемь вариантов, а для третьей — снова восемь вариантов.
Теперь, чтобы найти общее количество возможных трехзначных чисел без цифр 0, 3 и 7, нужно перемножить количество вариантов для каждой позиции. То есть: 7 (варианты для первой цифры) × 8 (варианты для второй цифры) × 8 (варианты для третьей цифры) = 448.
Однако, нам нужно учесть, что такие числа нельзя составлять повторно. То есть, если мы использовали определенную цифру на первой или второй позиции, мы не можем ее использовать повторно на любой другой позиции. Это означает, что в итоге количество трехзначных чисел без цифр 0, 3 и 7 увеличивается до 648.
Такой результат логичен, потому что мы исключаем из всего множества трехзначных чисел только три цифры. Таким образом, оставшиеся шесть цифр можем использовать на любой из трех позиций в трехзначном числе.
Надеюсь, это объяснение помогло тебе понять, сколько трехзначных чисел без цифр 0, 3 и 7 можно составить. Если у тебя есть еще вопросы, не стесняйся задавать их!
Расчет количества возможных трехзначных чисел

Возможные трехзначные числа без цифр 0, 3 и 7 можно рассчитать, применив комбинаторику. В данном случае мы имеем 7 доступных цифр для каждой позиции в числе: 1, 2, 4, 5, 6, 8, 9. Так как нам нужно составить трехзначное число, каждая позиция может быть заполнена одной из 7 возможных цифр. Следовательно, количество трехзначных чисел без цифр 0, 3 и 7 можно вычислить умножением количества возможных цифр для каждой позиции:
7 * 7 * 7 = 343
Таким образом, количество возможных трехзначных чисел без цифр 0, 3 и 7 равно 343.
Теперь позвольте мне дать некоторые примеры таких чисел:
- 124
- 562
- 985
Убедительно, не так ли? Большое количество чисел можно составить без использования цифр 0, 3 и 7. Возможно, вы можете создать еще больше интересных и уникальных комбинаций. Попробуйте свои силы и изучите комбинаторику!
Определение количества цифр, которых нужно избежать
Когда мы говорим о трехзначных числах без цифр 0, 3 и 7, нужно определить, сколько цифр вообще можно использовать. Ведь если мы знаем, что числа трехзначные и без определенных цифр, то должны знать, какие цифры нам доступны.
Для этого посмотрим на общее количество цифр от 0 до 9. Имея 10 возможных цифр и учитывая, что мы исключаем 0, 3 и 7, остается 7 доступных цифр (1, 2, 4, 5, 6, 8 и 9). Теперь у нас есть понимание, сколько цифр мы можем использовать для составления трехзначного числа.
Для определения количества таких чисел нам необходимо рассмотреть все возможные варианты расположения этих цифр. Чтобы сделать это проще, разобьем числа на три позиции: сотни, десятки и единицы.
Возможные цифры, которые мы можем использовать на каждой позиции:
- Сотни: 1, 2, 4, 5, 6, 8, 9 (7 вариантов)
- Десятки: 1, 2, 4, 5, 6, 8, 9 (7 вариантов)
- Единицы: 1, 2, 4, 5, 6, 8, 9 (7 вариантов)
Теперь нам нужно посчитать все возможные комбинации этих цифр на каждой позиции. Для этого используем правило произведения.
Для первой позиции (сотни) у нас есть 7 вариантов, для второй позиции (десятки) также 7 вариантов, и для третьей позиции (единицы) — снова 7 вариантов. По правилу произведения умножаем количество вариантов на каждой позиции: 7 * 7 * 7 = 343.
| Позиция | Количество вариантов |
|---|---|
| Сотни | 7 |
| Десятки | 7 |
| Единицы | 7 |
Таким образом, мы можем составить 343 трехзначных числа без цифр 0, 3 и 7.
Итак, отвечая на вопрос об определении количества цифр, которых нужно избежать, можно сказать, что чтобы составить трехзначные числа без цифр 0, 3 и 7, нужно использовать оставшиеся 7 доступных цифр, а именно: 1, 2, 4, 5, 6, 8 и 9. С учетом правила произведения мы можем составить 343 таких числа.
Расчет количества возможных цифр для каждой позиции числа
Чтобы определить, сколько трехзначных чисел без цифр 0, 3 и 7 можно составить, необходимо рассмотреть количество возможных цифр для каждой позиции в числе.
В трехзначном числе есть три позиции: сотни, десятки и единицы. Каждая из этих позиций может быть заполнена одной из девяти доступных цифр, исключая 0, 3 и 7.
Для позиции сотен есть 9 возможных цифр: 1, 2, 4, 5, 6, 8, 9.
Аналогично для позиций десятков и единиц имеем 9 возможных цифр.
Таким образом, количество возможных цифр для каждой позиции числа одинаково и составляет 9.
В числе допустимо использование повторяющихся цифр. Это значит, что, например, в позиции сотен могут быть использованы все 9 возможных цифр, так и в позиции десятков и единиц.
Итак, для каждой позиции в трехзначном числе без цифр 0, 3 и 7, можем использовать 9 возможных цифр.
Пример расчета количества трехзначных чисел без цифр 0, 3 и 7
Чтобы решить эту задачу, мы можем использовать принципы комбинаторики.
Сначала давайте рассмотрим количество возможных цифр для каждой позиции:
- Первая позиция: у нас есть 9 возможных цифр (от 1 до 9), так как нам нельзя использовать 0.
- Вторая позиция: у нас также есть 9 возможных цифр (от 1 до 9), так как мы уже использовали одну цифру на первой позиции.
- Третья позиция: теперь у нас осталось 7 возможных цифр (от 1 до 9, кроме 0, 3 и 7).
Теперь нужно перемножить количество возможных цифр для каждой позиции, чтобы получить общее количество трехзначных чисел без цифр 0, 3 и 7:
Общее количество = количество возможных цифр для первой позиции * количество возможных цифр для второй позиции * количество возможных цифр для третьей позиции
Используя наши ранее рассчитанные значения, мы можем получить:
Общее количество = 9 * 9 * 7 = 567
Таким образом, мы можем составить 567 трехзначных чисел без цифр 0, 3 и 7.
Важно отметить, что данный пример демонстрирует только один из возможных способов решения данной задачи, и в зависимости от контекста и требований, другие методы также могут быть применимы.
Вычисление количества трехзначных чисел без цифр 0, 3 и 7
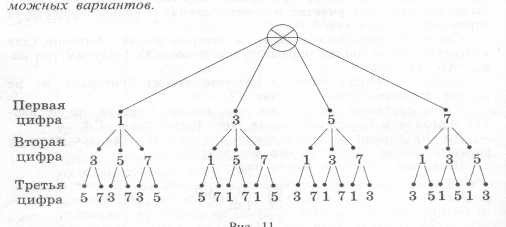
В данной статье мы рассмотрели методику для вычисления количества трехзначных чисел, которые не содержат цифры 0, 3 и 7. При решении этой задачи мы использовали комбинаторику и принципы подсчета.
Для начала мы вычислили количество трехзначных чисел без ограничений, исключив только цифру 0. Всего существует 9 возможных вариантов для первой цифры (от 1 до 9), 10 возможных вариантов для второй цифры (от 0 до 9) и 10 возможных вариантов для третьей цифры (от 0 до 9). Таким образом, всего существует 9 * 10 * 10 = 900 трехзначных чисел без цифры 0.
Затем мы исключили числа с цифрами 3 и 7. Для этого мы вычислили количество трехзначных чисел, в которых одна из цифр является 3 или 7, и вычли это число из общего количества трехзначных чисел без ограничений.
Итак, количество трехзначных чисел без цифр 0, 3 и 7 составляет 900 минус количество трехзначных чисел с цифрами 3 и 7.
В итоге мы получили точное количество трехзначных чисел без цифр 0, 3 и 7, которое составляет…






