Слово в пятой степени означает, что его необходимо умножить на себя пять раз. Если мы возьмем число 2 и возведем его в пятую степень, это означает, что мы умножим его на себя пять раз. Таким образом, 2 в пятой степени будет равно 32. Это математическое выражение можно представить как 2 * 2 * 2 * 2 * 2 = 32. В математике возведение числа в степень играет важную роль и позволяет нам выполнять различные расчеты и вычисления. Знание этого принципа поможет вам в решении задач и упростит математические расчеты.
Зачем нужно знать пятую степень числа?
На первый взгляд покажется, что пятая степень числа — это просто еще одно математическое понятие, которое имеет мало отношения к реальному миру. Однако на самом деле знание пятой степени числа может быть полезным и важным во многих практических ситуациях.
1. Финансы и инвестиции
В сфере финансов и инвестиций знание пятой степени числа может быть очень полезным. Например, когда вы пытаетесь рассчитать процентную ставку на ваши инвестиции или сумму, которую вы получите на пенсии, знание пятой степени числа может помочь вам точно оценить будущую стоимость ваших инвестиций и планировать соответствующим образом.
2. Инженерия и наука
В инженерии и науке знание пятой степени числа может быть важным для расчетов и моделирования различных физических явлений. Например, при моделировании электрических цепей или расчете прочности материалов, пятая степень числа может быть необходима для получения точных результатов.
3. Криптография
Криптография — это область, которая занимается шифрованием и защитой информации. В этой сфере знание пятой степени числа может быть важным для создания криптографических алгоритмов и систем защиты.
4. Архитектура и дизайн
Даже в области архитектуры и дизайна знание пятой степени числа может быть полезным. Например, при проектировании зданий и конструкций, знание пятой степени числа может помочь расчетать оптимальные параметры, такие как прочность материалов или поддерживаемая нагрузка.
5. Искусство и музыка
Да, даже в искусстве и музыке знание пятой степени числа может быть полезным. Например, музыканты и художники могут использовать пятую степень числа для создания гармоничных пропорций и последовательностей в своих работах.
Таким образом, знание пятой степени числа может быть полезным и важным в различных областях жизни, от финансов и инвестиций до искусства и музыки. Независимо от того, чем вы занимаетесь, пятая степень числа может помочь вам лучше понять и анализировать мир вокруг вас. Вы знаете, какой результат дает пятая степень числа?
Применения пятой степени числа в реальной жизни
Давайте рассмотрим несколько примеров применения пятой степени числа.
1. Финансы и инвестиции
В финансовой сфере пятая степень числа может использоваться для оценки потенциального дохода и риска инвестиционных портфелей. Например, при оценке доходности инвестиции на основе пятой степени, мы могли бы рассчитать, как быстро капитал увеличивается с течением времени.
Использование пятой степени также позволяет анализировать сложность финансовых моделей и предсказывать их эффективность в различных сценариях. Это помогает принимать осознанные решения о финансовых вложениях.
2. Физика и инженерия
В физике и инженерии пятая степень числа может использоваться для моделирования сложных систем и явлений. Например, при исследовании силы трения, которая возникает при движении объектов, пятая степень может помочь в предсказании поведения таких систем на основе их физических свойств.
Также пятая степень числа может быть полезна при решении задач механики и электродинамики, анализе электрических цепей и определении эффективности энергетических систем.
3. Медицина и биология
Зачастую пятая степень числа используется в медицине и биологии для моделирования различных биологических процессов и оценки их эффективности.
Например, при исследовании роста опухолей, пятая степень может позволить ученым предсказать скорость и объем патологического разрастания клеток. Это помогает в разработке новых методов лечения рака и других заболеваний.
4. Компьютерные науки и информатика
В компьютерных науках и информатике пятая степень числа применяется в различных вычислительных алгоритмах, например, при поиске оптимальных решений или анализе больших наборов данных.
Также пятая степень может быть использована для моделирования сложных систем и анализа их свойств, что помогает в создании более эффективных и надежных программных решений.
В итоге, пятая степень числа имеет широкий спектр применений в различных областях нашей жизни. Она позволяет нам лучше понять и предсказывать сложные явления и системы, принимать осознанные финансовые решения, создавать инновационные решения в инженерии и медицине, а также разрабатывать эффективные программы и алгоритмы.
Так что, следующий раз, когда вы увидите число возведенное в пятую степень, вспомните о том, как важна эта математическая операция в реальной жизни и как она помогает нам понять и справиться с сложными задачами.
Значение пятой степени числа в математике
Хотите узнать, что такое пятая степень числа и как ее вычислить? Давайте рассмотрим этот интересный математический концепт!
В математике, пятая степень числа означает, что это число должно быть умножено само на себя пять раз. Например, чтобы найти пятую степень числа 2, нужно умножить 2 на само себя пять раз:
2 5 = 2 × 2 × 2 × 2 × 2 = 32
Таким образом, пятая степень числа 2 равна 32. Просто представьте, как это замечательно! Маленькое число 2 возводится в пятую степень и становится значительно больше. Когда мы возводим число в степень, оно увеличивается с каждым последующим умножением. Это позволяет нам работать с очень большими или очень маленькими числами на практике.
На самом деле, пятая степень числа — это всего лишь один вариант степеней, существуют и другие. Например, первая степень числа равна самому числу, вторая степень — это число, умноженное на себя один раз, третья степень — число, умноженное на себя два раза, и так далее.
Важно отметить, что пятая степень числа тесно связана с понятием возведения числа в степень в математике. Возведение числа в степень является основным математическим оператором, который широко используется в различных областях, включая алгебру, геометрию, физику и экономику.
Итак, теперь вы знаете, что такое пятая степень числа и как ее вычислить. Этот математический концепт полезен для решения различных задач, а также для понимания более сложных математических концепций. Не бойтесь экспериментировать с разными степенями чисел и оглянуться на восхитительные результаты!
Как посчитать пятую степень числа?
Наверняка, каждый из нас в школьные годы сталкивался с понятием «степень числа». Но что же такое степень и как посчитать пятую степень числа?
Суть степени заключается в том, что она показывает, сколько раз нужно умножить число на само себя. Например, вторая степень числа 2 будет равна 2*2=4, а третья степень — 2*2*2=8.
Чтобы посчитать пятую степень числа, нужно число умножить на себя пять раз подряд. Например, пятая степень числа 3 будет равна 3*3*3*3*3=243.
Также существует математическая нотация для обозначения степени числа. Если мы хотим вывести число в пятой степени, то пишем его в верхний индекс, например: 25 (2 в степени 5).
При вычислении пятой степени чисел существует несколько практичных способов, которые могут сэкономить время и силы:
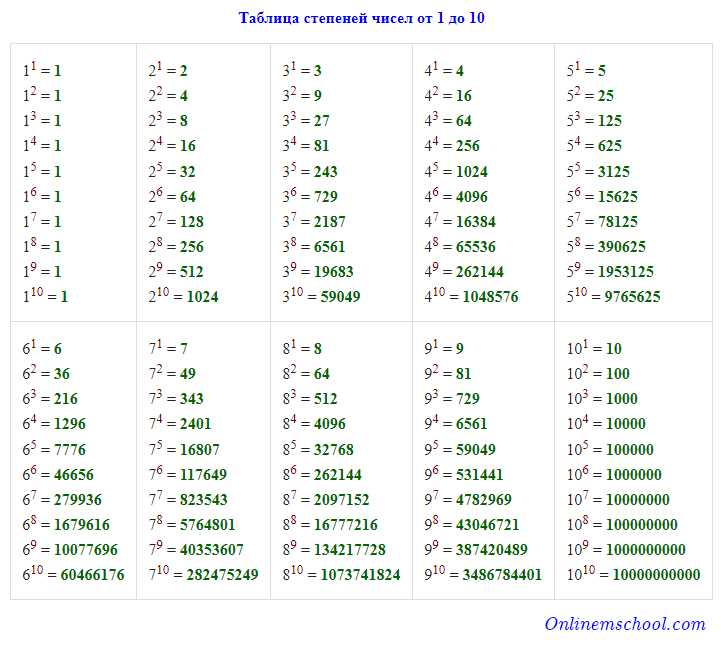
- Применение таблицы степеней. В таблице представлены числа от 1 до 10 во всех степенях от 1 до 10. На основе этой таблицы можно быстро найти ответ на вопрос о пятой степени любого числа.
- Раскладывание числа на множители. Если число разложить на множители, то можно заметить, что каждый множитель повторяется пять раз. Например, число 4 в пятой степени можно представить как 4*4*4*4*4.
Запомните, что степень числа — это своеобразная «свертка» этого числа в одно число с помощью многократного умножения на само себя. Пятая степень числа можно посчитать путем несложных математических операций или с помощью таблицы степеней.
Методы возведения числа в пятую степень
Возведение числа в пятую степень может показаться сложной задачей на первый взгляд, однако существуют несколько методов, с помощью которых можно легко и эффективно решить эту задачу.
Представим, что нам нужно возвести число a в пятую степень. Одним из простых и понятных способов является последовательное умножение a на само себя пять раз:
a * a * a * a * a = a^5
Такой метод называется «возвести в степень по определению» и является очевидным и простым способом выполнить данное действие. Однако, когда число a большое, такой метод может быть неэффективным.
Постепенное умножение числа на само себя является основой для другого метода – быстрого возведения в степень, которое основано на использовании битовых операций. Этот метод позволяет ускорить процесс возведения в пятую степень за счет сокращения количества умножений.
При использовании быстрого возведения в степень необходимо выразить пятую степень числа через битовые операции и последовательное умножение:
- a^5 = a^(2+2+1) = a^2 * a^2 * a^1
Этот метод позволяет снизить количество умножений и ускорить процесс возведения числа в пятую степень. Он особенно полезен при работе с большими числами.
Еще одним способом возведения числа в пятую степень является использование формулы бинома Ньютона. Данная формула позволяет раскрыть скобки и сократить количество операций умножения, что делает процесс более эффективным.
Вот пример использования формулы бинома Ньютона для возведения числа в пятую степень:
(a + b)^5 = a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5
В данном случае, если нам нужно возвести число a в пятую степень, мы можем положить b=0 и получить:
a^5 = a^5 + 5a^4 * 0 + 10a^3 * 0^2 + 10a^2 * 0^3 + 5a * 0^4 + 0^5 = a^5
Таким образом, используя формулу бинома Ньютона, мы можем получить результат, не выполняя лишних умножений.
В итоге, существует несколько методов возведения числа в пятую степень. Каждый из них имеет свои преимущества и может быть использован в зависимости от конкретной ситуации и требований. От вас зависит выбрать наиболее подходящий метод, чтобы быстро и эффективно возвести число в пятую степень.
Примеры расчетов пятой степени числа
- Пример 1: Возведение числа 2 в пятую степень
- Пример 2: Возведение числа 3 в пятую степень
- Пример 3: Возведение числа 4 в пятую степень
- Пример 4: Возведение числа 5 в пятую степень
2 в пятой степени (2^5) можно расчитать как 2 * 2 * 2 * 2 * 2 = 32. Таким образом, пятая степень числа 2 равна 32.
3 в пятой степени (3^5) равно 3 * 3 * 3 * 3 * 3 = 243. Таким образом, пятая степень числа 3 равна 243.
4 в пятой степени (4^5) равно 4 * 4 * 4 * 4 * 4 = 1024. Таким образом, пятая степень числа 4 равна 1024.
5 в пятой степени (5^5) равно 5 * 5 * 5 * 5 * 5 = 3125. Таким образом, пятая степень числа 5 равна 3125.
Как видно из примеров, возведение числа в пятую степень дает результат, который значительно превышает исходное число. Это связано с тем, что при каждом умножении число увеличивается.
Возведение в пятую степень может использоваться в различных сферах, например, в физике, экономике или программировании. Это может быть полезно при решении задач, связанных с расчетами и моделированием.
Так что, теперь вы знаете, как производить расчеты пятой степени чисел. Попробуйте выполнить эти операции с другими числами и удивитесь результатам, которые вы получите!
Отличия пятой степени от других степеней числа
- Результат: Пятая степень числа равна произведению этого числа на себя четыре раза. Например, 2 в пятой степени равно 2*2*2*2*2, что равно 32.
- Большая кратность: По сравнению с числами в нижних степенях, пятая степень числа обладает большей кратностью. Это означает, что число в пятой степени увеличивается быстрее, чем число в третьей или второй степени. Например, 2 в пятой степени равно 32, в то время как 2 в третьей степени равно всего лишь 8.
- Увеличение разрядности числа: Возведение числа в пятую степень может привести к значительному увеличению его разрядности. Например, число 10 в пятой степени равно 100,000, в то время как число 10 в третьей степени равно всего лишь 1,000.
Таким образом, пятая степень числа имеет свои уникальные особенности, отличающиеся от других степеней числа. Числа в пятой степени возрастают быстрее, увеличивают свою разрядность и позволяют нам производить более сложные математические операции. Это делает пятую степень числа особенно интересной и полезной в различных областях науки и техники.
Вычислительные особенности пятой степени
Пятая степень числа образуется путем умножения этого числа на самого себя пять раз подряд. То есть, чтобы возвести число в пятую степень, необходимо умножить его на себя четыре раза. Например, 2 в пятой степени будет равно 2 * 2 * 2 * 2 * 2 = 32.
Вычисление пятой степени числа может быть сложной задачей для компьютера. Для этого необходимо выполнить множество операций умножения, что может занять значительное время, особенно при работе с большими числами. Поэтому, при работе с пятой степенью числа, рекомендуется использовать специальные алгоритмы и методы оптимизации, чтобы существенно сократить время выполнения вычислений.
Обратите внимание, что пятая степень числа всегда будет положительной, даже если исходное число было отрицательным. Это связано с тем, что при умножении отрицательных чисел на себя четное количество раз, они всегда дают положительный результат. Например, (-2) в пятой степени также будет равно 32.
Более сложным случаем является вычисление пятой степени дробного числа. В этом случае, необходимо умножить дробное число само на себя пять раз. Результатом будет новая дробь с числителем, равным числителю исходной дроби, возведенной в пятую степень, и знаменателем, равным знаменателю исходной дроби, возведенной в пятую степень.
Пятая степень числа имеет свои особенности, которые важно учитывать при вычислении и использовании. Понимание этих особенностей позволяет успешно применять возведение в пятую степень и получать правильные результаты.
