Сколько будет 10 в минус первой степени? Это интересный вопрос, на который мы сейчас найдем ответ. Если мы возьмем число 10 и возведем его в степень -1, то получим новое число, которое будет являться обратным значением числа 10. В математике обратное значение числа a обозначается как 1/a. То есть, когда мы возведем 10 в минус первую степень, получаем: 1/10. А это означает, что результат будет равен 0.1. Таким образом, 10 в минус первой степени равняется 0.1. Если у вас остались сомнения, проверьте это значение с помощью калькулятора или обратитесь к математическим источникам для уточнения данного факта.
Определение степени
Для примера, рассмотрим число 2. Когда мы говорим, что число 2 возводится в степень, мы умножаем его само на себя несколько раз. Если мы возведем 2 во вторую степень, получим 2 * 2 = 4. Возведение в третью степень даст нам 2 * 2 * 2 = 8, и так далее. Чем выше степень, тем больше раз мы умножаем число на себя.
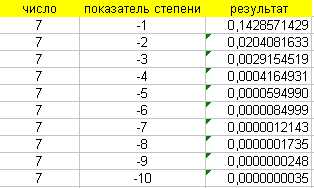
В данном случае, ты спросил, сколько будет 10 в минус первой степени. Если мы возведем 10 в минус первую степень, получим 1/10. Простыми словами, мы берем число 10 и делим его на само себя один раз. Это дает нам результат, который равен 0.1 или одной десятой.
Итак, когда ты задаешь вопрос о том, сколько будет 10 в минус первой степени, ответом будет 0.1 или 1/10.
Что такое степень числа?

Например, если мы имеем число 5 в степени 3, то это означает, что мы должны умножить число 5 на само себя три раза. То есть 5 * 5 * 5 = 125.
Степень числа может быть как положительной, так и отрицательной. Положительная степень означает, что мы должны умножить число на само себя несколько раз, а отрицательная степень означает, что мы должны разделить число на само себя несколько раз.
Когда мы имеем число в отрицательной степени, мы можем записать его в виде десятичной дроби. Например, число 5 в минус первой степени можно записать как 1/5 (чтобы получить этот ответ, мы делим 1 на 5).
Если мы возведем число в отрицательную степень, то получим десятичную дробь, а если возведем в положительную степень, то получим целое число или большее число.
Итак, возвращаясь ко вопросу, сколько будет 10 в минус первой степени, мы можем записать это число как 1/10. Таким образом, ответ равен 1/10.
Как обозначается степень числа?
Степени чисел являются основой для математических вычислений и имеют множество применений в нашей повседневной жизни. Например, они используются в науке, физике, экономике и многих других областях.
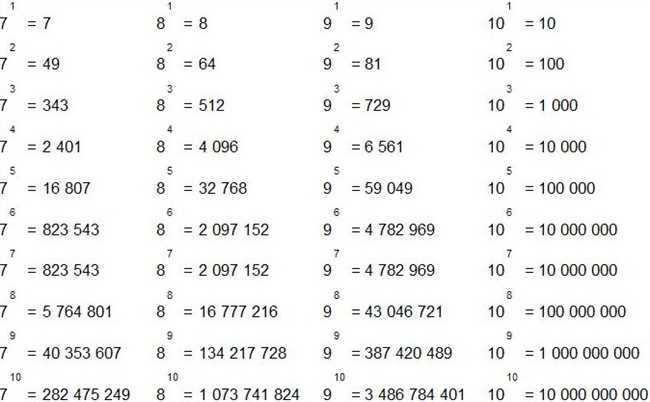
Когда число возводится в положительную целочисленную степень, результат получается путем повторного умножения числа на само себя. Например, чтобы найти результат 103 (10 в степени 3), нужно умножить число 10 на само себя три раза: 10 × 10 × 10 = 1000.
Если число возводится в отрицательную степень, то результат получается путем деления единицы на число, возведенное в положительную степень. Например, чтобы найти результат 10-2 (10 в минус второй степени), нужно поделить единицу на 10, возведенное во вторую степень: 1 / (10 × 10) = 0.01.
Таким образом, когда мы говорим о степенях чисел, мы указываем, сколько раз число умножается само на себя или делится на себя, в зависимости от знака степени. Используя эти математические операции, мы можем решать различные задачи и находить решения в различных областях знаний.
Отрицательная степень
Все дело в том, что отрицательная степень – это обратная величина положительной степени. Например, 2 в квадрате равно 4, а 2 в минус квадрате равно 1/4. То есть отрицательная степень выражает обратное значение числа. Поэтому в случае возведения числа в отрицательную степень мы должны получить десять в обратной степени.
Теперь мы можем перейти к самому вопросу: «Сколько будет 10 в минус первой степени?». Для ответа на этот вопрос нам необходимо знать одно важное правило: любое число, возведенное в отрицательную первую степень, равно 1 деленное на это число. То есть 10 в минус первой степени будет равно 1/10 или 0,1.
Если у нас возникает другая задача, например, найти результат возведения числа в отрицательную степень с использованием десятичной системы и отрицательной степенью больше одного, то можно воспользоваться обратным правилом возведения чисел в степень. Например, 2 в минус третьей степени будет равно 1/(2*2*2) или 1/8.
Отрицательная степень является важным и неотъемлемым понятием в математике, она позволяет нам находить обратные значения чисел и решать разнообразные задачи. Поэтому не бойтесь отрицательных степеней и используйте их в своих расчетах.
Что такое отрицательная степень?
Чтобы лучше понять это понятие, давай рассмотрим простой пример: возведение числа 2 в отрицательную степень:
2 в минус первой степени обозначается как 2-1. Чтобы найти результат, мы должны разделить единицу на число, возведенное в положительную степень. То есть:
2-1 = 1 / 21 = 1/2 = 0,5
Таким образом, 2 в минус первой степени равно 0,5.
Отрицательная степень может быть полезной при решении различных задач. Например, если мы знаем, что 2 возводится в положительную степень равную 3, то можем использовать отрицательную степень, чтобы найти результат в виде десятичной дроби. То есть:
23 = 8
2-3 = 1 / 23 = 1/8 = 0,125
Таким образом, отрицательная степень позволяет нам работать с числами в форме десятичной дроби, что может быть полезным при решении различных задач.
Свойства отрицательной степени
- Инверсия значения: Отрицательная степень числа равна обратному значению того числа в положительной степени. Например, 10 в минус первой степени равно 1/10.
- Изменение порядка: При возведении числа в отрицательную степень изменяется порядок числа. Например, если число равно 2, то 2 в минус второй степени будет равно 1/4.
- Сохранение знака: При возведении числа в отрицательную степень его знак сохраняется. Например, (-2) в минус третьей степени будет равно -1/8.
Отрицательная степень имеет важное значение в математике и широко применяется в различных областях, включая физику, экономику и программирование. Понимание свойств отрицательной степени поможет лучше разобраться в работе с числами и решении математических задач.






