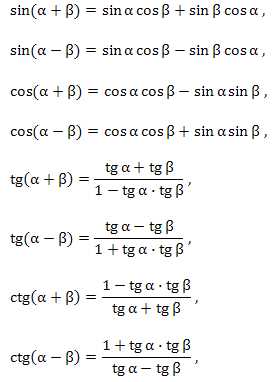
Синус 2х — это математическая функция, которая широко используется в различных областях, таких как физика, инженерия и компьютерная графика. Она является основной тригонометрической функцией, определенной отношением противоположного катета к гипотенузе прямоугольного треугольника. Формула для расчета синуса 2х выглядит следующим образом: sin(2x) = 2 * sin(x) * cos(x), где x — значение угла. Расчеты с использованием этой формулы позволяют нам определить значения синуса угла 2х на основе известного значения синуса угла x. Знание формулы синуса 2х и умение выполнять соответствующие расчеты являются важными навыками в решении задач, связанных с тригонометрией и техническими науками.
Раздел 1: Что такое синус 2x
Но как мы можем понять, что же это за функция и как ее использовать? Давайте рассмотрим это подробнее.
Синус 2x представляет собой отношение длины противоположного катета к гипотенузе прямоугольного треугольника. Также он можно определить с помощью ряда Тейлора или комплексных чисел.
Синус 2x обозначается как sin(2x) или сокращенно как sin2x. Здесь 2x — угол, выраженный в радианах.
Основные свойства синуса 2x:
- Периодичность: функция sin2x повторяет себя через равные интервалы, когда аргумент увеличивается или уменьшается на целое число угловых единиц 2π (или 360 градусов).
- Значение: синус 2x может принимать значения между -1 и 1. Это связано с определением функции через противоположный катет и гипотенузу прямоугольного треугольника.
- Амплитуда: синус 2x имеет амплитуду 1, что означает, что его значения колеблются между -1 и 1.
Теперь, когда вы знакомы с основными понятиями и свойствами синуса 2x, вы можете использовать его в различных математических и физических расчетах. Например, функция sin2x может быть полезна при анализе колебаний, волновых процессов или решении уравнений.
Не забывайте, что практика делает совершенство. Чем больше вы будете практиковаться в расчетах с синусом 2x, тем лучше вы станете в его использовании и применении в реальных задачах.
Общие сведения о синусе 2x
Синус 2x можно выразить через обычный синус x с использованием формулы двойного угла. Формула для синуса двойного угла имеет следующий вид:
sin(2x) = 2sin(x)cos(x)
То есть, чтобы найти значение синуса угла 2x, необходимо умножить синус угла x на косинус угла x и умножить полученный результат на 2. Важно отметить, что эта формула основана на тригонометрической идентичности.
Применение данной формулы может быть полезным при подсчете значений синуса 2x для различных углов. Например, если известно значение синуса угла x, можно легко найти значение синуса угла 2x с помощью формулы.
Также стоит отметить, что синус 2x обладает некоторыми свойствами, которые могут быть полезны при анализе графиков или решении уравнений. Например:
- Синус 2x имеет период, равный периоду обычного синуса, то есть 2π.
- Синус 2x симметричен относительно оси OY, что означает, что его график является четным.
Общие сведения о синусе 2x могут быть полезны не только для изучающих математику, но и для всех, кто интересуется применением данной функции в практических задачах. Знание основных свойств и формул позволяет более эффективно использовать синус 2x при решении различных задач и заданий.
Примеры вычисления синуса 2x

Вычисление синуса 2x может быть полезным при решении различных задач, связанных с тригонометрией, физикой или инженерными расчетами. Рассмотрим несколько примеров, чтобы проиллюстрировать этот процесс.
Пример 1:
Предположим, что нам нужно вычислить значение синуса угла в два раза большего, чем заданный угол. Допустим, у нас есть угол x, равный 30 градусам (π/6 радиан). Чтобы найти синус 2x, мы можем воспользоваться формулой:
син 2x = 2sinx*cosx
В нашем случае:
- sin(2 * 30 градусов) = 2 * sin(30 градусов) * cos(30 градусов)
- sin(60 градусов) = 2 * (1/2) * (√3/2)
- √3/2
Таким образом, синус 2x в данном случае равен √3/2.
Пример 2:
Допустим, нам нужно вычислить значение синуса двойного угла, если известен синус самого угла. Представим, что sin(x) = 1/2, а мы хотим найти sin(2x).
Мы можем воспользоваться формулой:
син 2x = 2sinx*cosx
В нашем случае:
- sin(2x) = 2 * (1/2) * √(1 — (1/2)^2)
- sin(2x) = √(1 — 1/4)
- sin(2x) = √(3/4)
- sin(2x) = √3/2
Итак, sin(2x) равен √3/2.
Пример 3:
Предположим, у нас есть угол x, равный π/4 радиан (или 45 градусов), и мы хотим найти значение sin(2x).
Мы можем использовать формулу:
син 2x = 2sinx*cosx
В нашем случае:
- sin(2 * π/4) = 2 * sin(π/4) * cos(π/4)
- sin(π/2) = 2 * (1/√2) * (1/√2)
- 1 = 1/2
Таким образом, sin(2x) равен 1/2.
В этом кратком обзоре мы представили несколько примеров вычисления синуса 2x. Наша цель была продемонстрировать, как применять формулу синуса двойного угла и получать точные значения для различных углов. Ответы, которые мы получили, иллюстрируют применение тригонометрии в различных областях и помогают нам лучше понять математический аспект углов и их свойств.
Раздел 2: Формула для расчета синуса 2x
Когда мы говорим о синусе угла 2x, мы обычно имеем в виду функцию sin(2x), которая определяется следующей формулой:
sin(2x) = 2sin(x)cos(x)
Эта формула позволяет нам выразить синус угла 2x через синус и косинус самого угла x. Она основана на тождестве двойного угла для синуса, которое гласит:
sin(2x) = 2sin(x)cos(x)
Давайте рассмотрим пример, чтобы увидеть, как использовать эту формулу. Представим, что у нас есть угол x, равный 30 градусам. Мы хотим найти значение sin(60 градусов), что соответствует синусу угла 2х.
Сначала мы можем использовать формулу для нахождения sin(2x):
sin(2x) = 2sin(x)cos(x)
Подставляя значение угла x (30 градусов), мы получаем:
sin(60 градусов) = 2sin(30 градусов)cos(30 градусов)
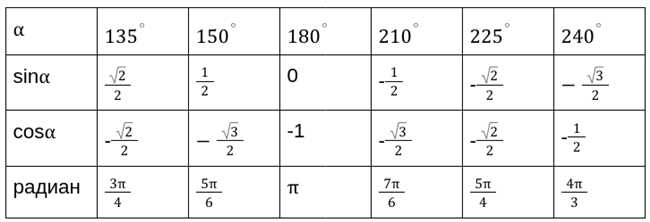
Далее нам нужно знать значения синуса и косинуса 30 градусов. Мы можем использовать таблицу значений тригонометрических функций или калькулятор для получения этих значений. В данном случае, sin(30 градусов) равен 0.5, а cos(30 градусов) равен √3/2.
Подставляя значения в формулу, мы получаем:
sin(60 градусов) = 2 * 0.5 * √3/2 = √3/2
Таким образом, sin(60 градусов) равен √3/2.
Как видите, использование формулы для расчета синуса 2x может быть полезным при работе с углами и их тригонометрическими функциями. Эта формула позволяет нам связать синус угла 2x с синусом и косинусом самого угла x, что упрощает вычисления и облегчает работу с тригонометрическими функциями.
Основная формула синуса 2x
Формула синуса 2x имеет следующий вид:
sin(2x) = 2 * sin(x) * cos(x)
Где:
- sin(2x) — значение синуса удвоенного угла;
- sin(x) — значение синуса исходного угла;
- cos(x) — значение косинуса исходного угла.
Формула позволяет найти значение синуса удвоенного угла, зная значение синуса и косинуса исходного угла. Также она может быть использована для выражения синуса и косинуса удвоенного угла через синус и косинус исходного угла.
Знание основной формулы синуса 2x позволяет не только решать задачи, связанные с углами, но и более глубоко понимать связь между углами и их тригонометрическими функциями.
Свойства формулы синуса 2x
Формула синуса 2x выражает значение синуса угла, удвоенного по отношению к исходному углу x. Эта формула имеет несколько свойств, которые могут быть полезны в различных математических и физических вычислениях.
1. Удвоение аргумента. Значение синуса 2x равно двукратному произведению синуса угла x на косинус угла x.
Синус 2x = 2 * sin(x) * cos(x)
Это свойство может быть использовано для упрощения вычислений, особенно при работе с углами, кратными 30, 45 и 60 градусам.
2. Периодичность. Формула синуса 2x также обладает свойством периодичности. Значение функции повторяется через определенные интервалы. В данном случае, период формулы синуса 2x равен половине периода формулы синуса x.
То есть, если период синуса x равен 2π, то период синуса 2x будет π.
3. Значение в особых точках. Формула синуса 2x имеет специальные значения в некоторых особых точках.
- Синус 2x равен нулю, когда аргумент 2x равен нулю, π или 2π.
- Синус 2x равен 1, когда аргумент 2x равен π/2.
- Синус 2x равен -1, когда аргумент 2x равен 3π/2.
Знание этих значений может быть полезно при вычислении определенных функций или нахождении корней уравнений, в которых присутствует синус 2x.
Раздел 3: Способы вычисления синуса 2x
В данном разделе были изучены различные способы вычисления синуса 2x. Зная значение угла x, можно легко найти его удвоение. Существуют несколько подходов к вычислению синуса 2x, каждый из которых имеет свои особенности и применение.
Один из наиболее распространенных способов вычисления синуса 2x — это использование формулы удвоения аргумента: sin(2x) = 2 * sin(x) * cos(x). Эта формула основана на разложении синуса двойного угла через синус и косинус угла x.
Второй способ вычисления синуса 2x — это использование формулы разности аргументов: sin(2x) = sin(x + x) = sin(x) * cos(x) + cos(x) * sin(x). При раскрытии скобок и применении тригонометрических тождеств мы получаем эту формулу.
Также существуют другие способы вычисления синуса 2x, например, метод тангенса: sin(2x) = 2 * tan(x) / (1 + tan^2(x)). Этот метод основан на связи синуса и тангенса угла.
Каждый из этих способов имеет свои преимущества и недостатки. Выбор конкретного метода зависит от задачи, которую нужно решить, и условий, в которых он будет применяться.






