- Обзор методов и правил чтения чисел с десятичной запятой
- 1. Правило тысячных
- 2. Правило десятичных
- 3. Правило процентов
- 4. Другие методы и правила
- Методы чтения чисел с десятичной запятой
- Чтение по цифрам
- Чтение по группам чисел с десятичной запятой: как не запутаться
- Правила чтения чисел с десятичной запятой
- 1. Основные правила чтения десятичных чисел:
- 2. Односложные числа после десятичной запятой:
- 3. Числа больше десяти после десятичной запятой:
- 4. Числа меньше единицы:
- 5. Округление чисел:
- 6. Научные записи чисел:
- Определение порядка разрядов
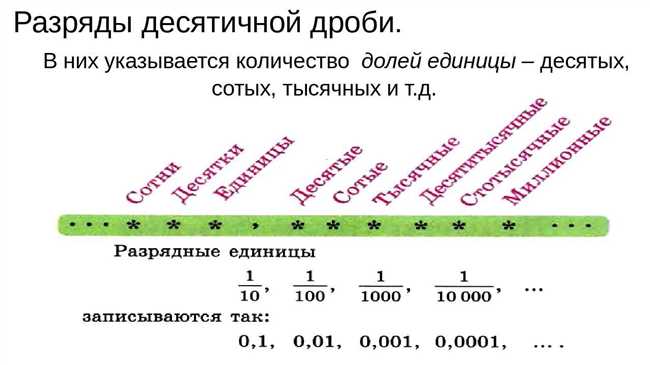
Когда мы сталкиваемся с числами, в которых присутствуют десятичные разделители, возникают вопросы о том, как правильно их читать. Существует несколько методов и правил, которые помогут нам разобраться с этой проблемой. Во-первых, мы можем просто использовать традиционный способ чтения чисел с десятичной запятой, где десятичные цифры считываются по отдельности. Во-вторых, мы можем использовать метод «четвертирующий», где дробная часть числа считывается как обычное число и умножается на число, обозначающее разрядность десятичной запятой. И, наконец, есть метод «смешанный», который сочетает в себе оба вышеуказанных метода. Каждый из этих методов имеет свои преимущества и недостатки, и выбор способа чтения числа с десятичной запятой зависит от контекста и предпочтений читателя.
Обзор методов и правил чтения чисел с десятичной запятой
Чтение чисел с десятичной запятой может иногда вызывать затруднения. Но не волнуйтесь, в этом обзоре мы разберем основные методы и правила чтения таких чисел, чтобы вы могли с легкостью разбираться с ними.
1. Правило тысячных
Одним из самых распространенных методов чтения чисел с десятичной запятой является использование правила тысячных. По этому правилу, целая и десятичная часть числа разделяются словом «целая» или «и». Например, число 3,14 можно прочитать как «три целых и четырнадцать сотых».
2. Правило десятичных
Другой метод чтения чисел с десятичной запятой основан на правиле десятичных. По этому правилу, десятичная часть числа читается отдельно от целой части. Например, число 3,14 можно прочитать как «три целых, запятая, одна четырнадцатая».
3. Правило процентов
Если вы имеете дело с процентными значениями, то есть специальное правило чтения таких чисел. По этому правилу, просто добавьте слово «процент» после числа. Например, число 50% можно прочитать как «пятьдесят процентов».
4. Другие методы и правила

Существуют и другие методы чтения чисел с десятичной запятой, которые могут использоваться в разных контекстах. Например, при чтении валютных значений может использоваться правило сокращений, а при чтении научных чисел — правило степеней.
Важно понимать, что правила чтения чисел с десятичной запятой могут немного отличаться в разных языках. Поэтому всегда имейте в виду, что контекст и специфика используемого языка могут влиять на выбор определенного метода или правила.
Методы чтения чисел с десятичной запятой
Чтение чисел с десятичной запятой может быть немного сложным для тех, кто не знаком с особенностями этого процесса. Однако существует несколько методов и правил, которые помогут вам справиться с этой задачей без особых проблем.
- Пошаговый подход: Один из самых простых методов чтения чисел с десятичной запятой состоит в том, чтобы разделить число на две части: целую и десятичную. Вначале прочтите целую часть числа, а затем десятичную, используя правила чтения отдельных цифр. Например, число 3,14 можно прочитать как «три целых четырнадцать сотых». Этот метод наиболее распространен и прост в использовании.
- Преобразование в дробь: Если вам сложно читать числа с десятичной запятой, вы можете преобразовать их в обычные дроби. Например, число 0,5 можно прочитать как «пять десятых» или как «одна вторая». Этот метод может быть полезен, если вам более привычно работать с обычными дробями.
- Замена запятой на «и»: Еще одним методом чтения чисел с десятичной запятой является замена запятой на слово «и». Например, число 2,7 можно прочитать как «два и семь десятых» или как «два и семь десятых». Этот метод может быть особенно полезен, когда вы читаете числа в тексте или пишете их словами.
Каждый из этих методов имеет свои преимущества и может быть полезен в разных ситуациях. Выберите тот, который вам наиболее удобен, и практикуйтесь в чтении чисел с десятичной запятой, чтобы стать еще более уверенным в этом навыке.
Чтение по цифрам
Чтение чисел с десятичной запятой может быть сложной задачей, особенно когда речь идет о больших и сложных числах. Однако есть способ, который облегчает эту задачу и делает чтение по цифрам более понятным и легким.
Представь, что тебе нужно прочитать число 3.14. Самый простой способ — прочитать его по цифрам. Первая цифра — 3, это три. Вторая цифра — 1, это один. Третья цифра — 4, это четыре. И последняя цифра — это 0, ноль. Итак, число 3.14 читается как «три целых четырнадцать сотых». Проще не бывает, правда?
А теперь представим, что у нас есть число 123.456. Прочитать его по цифрам немного сложнее, но все еще возможно. Первая цифра — 1, это один. Вторая цифра — 2, это два. Третья цифра — 3, это три. Четвертая цифра — 4, это четыре. Пятая цифра — 5, это пять. И последняя цифра — 6, это шесть. Таким образом, число 123.456 читается как «сто двадцать три целых, четыреста пятьдесят шесть тысячных».
Конечно, читать числа по цифрам может быть немного запутанным, особенно когда мы имеем дело с более сложными числами. В этом случае можно использовать таблицу или список, чтобы упростить процесс чтения.
- 1 — один
- 2 — два
- 3 — три
- 4 — четыре
- 5 — пять
- 6 — шесть
- 7 — семь
- 8 — восемь
- 9 — девять
- 0 — ноль
Таблица поможет тебе быстро определить, какое слово соответствует каждой цифре. Таким образом, ты сможешь с легкостью прочитать любое число, как большое, так и маленькое.
Итак, чтение по цифрам — это простой и эффективный способ читать числа с десятичной запятой. Независимо от сложности или размера числа, прежде всего определи каждую цифру и затем прочитай число поочередно. И не забудь использовать таблицу, если тебе нужно быстро определить, какое слово использовать для каждой цифры.
Чтение по группам чисел с десятичной запятой: как не запутаться
Метод чтения по группам основан на разбиении числа на отдельные группы цифр, разделенных запятыми. В результате получается более наглядное представление числа и легче его прочитать. Давайте разберемся, как это работает.
1. Первым шагом нужно определить, какие цифры находятся перед десятичной запятой. Это цифры, которые идут слева от запятой. Так, например, если у нас число 1,234.56, то перед запятой находится цифра 1.
2. Далее, нужно разбить цифры после запятой на группы по три числа. Если после запятой остается меньше трех цифр, то их считаем отдельной группой. Например, если у нас число 1,234.56, то после запятой есть две группы — 234 и 56.
3. Теперь можем приступить к чтению. Сначала произносим цифры перед запятой, затем первую группу после запятой, следующую за ней и так далее. Пример чтения числа 1,234.56: «Один тысяча двести тридцать четыре целых пятьдесят шесть сотых».
Чтение по группам помогает нам лучше представить и запомнить большие числа с десятичной запятой. Этот метод особенно полезен, когда число имеет много десятичных разрядов. Например, при обработке финансовых данных или при работе с большими измерениями в науке.
Запомните этот метод чтения чисел с десятичной запятой по группам и используйте его в своей повседневной жизни. Он поможет вам быть более точным и уверенным при работе с числами.
Правила чтения чисел с десятичной запятой
Чтение чисел с десятичной запятой может быть иногда непростой задачей, особенно если речь идет о больших или малых числах. В этом обзоре мы рассмотрим основные правила чтения таких чисел, которые помогут вам уверенно и точно читать десятичные числа в любой ситуации.
1. Основные правила чтения десятичных чисел:

- Перед десятичной запятой называется целая часть числа, например: 123 — сто двадцать три.
- После десятичной запятой называется дробная часть числа, например: 0.75 — ноль целых семьсот пятьдесят тысячных.
- Если целая часть числа отрицательная, то перед ней ставится слово «минус», например: -3.14 — минус три целых четырнадцать сотых.
2. Односложные числа после десятичной запятой:
Односложные числа после десятичной запятой обычно читаются как обычные числа от 1 до 9. Например, 0.5 — ноль целых пять десятых, 0.9 — ноль целых девять десятых.
3. Числа больше десяти после десятичной запятой:
Если число после десятичной запятой больше 10, то оно читается по частям. Например, 1.25 — одна целая двадцать пять сотых.
4. Числа меньше единицы:
Числа меньше единицы после десятичной запятой читаются с помощью знаменателей. Например, 0.75 — ноль целых семьсот пятьдесят тысячных, 0.125 — ноль целых, сто двадцать пять тысячных.
5. Округление чисел:
При чтении округленных чисел с десятичной запятой, мы обычно округляем число до ближайшего целого и применяем правила чтения для этого целого числа. Например, 3.7 округляется до 4 целых, и затем читается как «четыре».
6. Научные записи чисел:
В научных записях числа с десятичной запятой обычно записываются с помощью степени десяти. Например, 1.2 x 10^6 — одна целая два умножить на десять в шестой степени.
| Обычная запись | Научная запись | Чтение числа |
|---|---|---|
| 0.01 | 1 x 10^-2 | одна целая сто двадцать пять тысячных |
| 1000 | 1 x 10^3 | одна целая два умножить на десять в третьей степени |
| 0.000001 | 1 x 10^-6 | одна целая два умножить на десять в шестой степени |
Теперь вы знакомы с основными правилами чтения чисел с десятичной запятой и можете легко и точно прочитать любое число. Запомните эти правила и попрактикуйтесь в их использовании, чтобы стать настоящим экспертом в чтении десятичных чисел!
Определение порядка разрядов
Определение порядка разрядов играет важную роль при чтении чисел с десятичной запятой. Порядок разрядов показывает, какая степень десяти умножается на каждый разряд числа.
Для определения порядка разрядов необходимо обратить внимание на позицию запятой. Если запятая находится перед первым числом, то порядок разрядов будет положительным, если запятая находится после последнего числа, то порядок разрядов будет отрицательным. При этом, чем дальше от запятой находятся разряды, тем ниже их порядок.
Например, в числе 123.45 порядок разрядов будет положительным, так как запятая находится перед первым числом. Порядок разрядов будет увеличиваться с каждой позицией от запятой: первая позиция имеет порядок 0, вторая -1, третья -2 и т.д.
В числе 0.00789 порядок разрядов будет отрицательным, так как запятая находится после последнего числа. Порядок разрядов будет уменьшаться с каждой позицией от запятой: первая позиция после запятой имеет порядок -1, вторая -2, третья -3 и т.д.
Определение порядка разрядов является важным шагом при чтении чисел с десятичной запятой, так как позволяет правильно интерпретировать и понять значение каждого разряда в числе.






