
Если вам нужно найти объем куба, зная длину диагонали грани, то есть несколько способов решения этой задачи. Во-первых, можно использовать формулу, связывающую длину диагонали грани и объем куба. Во-вторых, можно разделить задачу на две части: найти длину ребра куба, а затем возвести ее в куб и получить объем. В-третьих, можно использовать теорему Пифагора, чтобы найти длину ребра куба, а затем вычислить его объем. Каждый из этих методов имеет свои особенности и может быть применим в разных ситуациях. Следуя одному из них, вы сможете легко найти объем куба, зная длину диагонали грани.
Определение диагонали грани и её связь с объёмом куба
Чтобы определить связь диагонали грани куба с его объемом, придётся вспомнить некоторые математические формулы. Объём куба можно вычислить, зная длину его ребра или длину диагонали грани.
Длина ребра куба и длина диагонали грани связаны следующим образом: в кубе с ребром a длина диагонали грани d выражается через длину ребра следующей формулой: d = a√2.
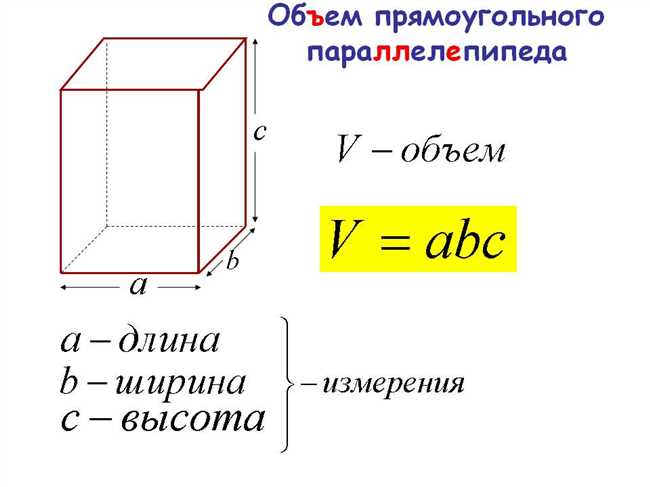
Теперь перейдём к вычислению объема куба. Объём куба можно найти по формуле V = a^3, где V — объём куба, а a — длина его ребра.
Связь диагонали грани и объёма куба можно определить, используя формулу для длины диагонали грани. Подставив формулу в формулу для нахождения объёма куба, получим V = (d/√2)^3.
Таким образом, если известна длина диагонали грани куба, то объем куба можно найти, возводя длину этой диагонали в куб и делая корень из получившегося числа, затем возводя в куб полученное значение.
Для лучшего понимания вычисления объёма куба по диагонали грани можно рассмотреть следующий пример:
- Пусть длина диагонали грани куба равна 5 см.
- Тогда согласно формуле d = a√2, где d — длина диагонали грани, а a — длина ребра, получим: 5 = a√2.
- Решив данное уравнение относительно a, получаем: a ≈ 5/√2 ≈ 3.54 см.
- Подставляя найденное значение ребра в формулу для объема куба V = a^3, получаем: V ≈ (3.54)^3 ≈ 44.63 см^3.
Таким образом, зная длину диагонали грани куба, мы можем вычислить его объем.
Примеры расчета объема куба при известной длине диагонали грани
Вы когда-нибудь задумывались о том, как найти объем куба, если вам известна только длина диагонали его грани? Несмотря на то, что вначале это может показаться сложной задачей, на самом деле это довольно просто.
Позвольте мне показать вам несколько примеров, чтобы вы лучше поняли, как это работает.
Пример 1:
Предположим, что длина диагонали грани куба составляет 10 сантиметров. Чтобы найти объем, вам нужно возвести длину этой диагонали в куб и разделить результат на 3.
Итак, для примера 1, мы будем иметь:
- Длина диагонали грани: 10 см
Теперь давайте посмотрим, как это выглядит в математической форме:
Объем = (Длина диагонали грани)^3 / 3
Подставим наши значения в формулу и получим:
Объем = (10 см)^3 / 3 = 1000 см³ / 3 = 333,33 см³
Таким образом, при длине диагонали грани 10 сантиметров, объем куба будет примерно равен 333,33 кубическим сантиметрам.
Пример 2:
Давайте рассмотрим еще один пример, чтобы лучше усвоить процесс. Пусть длина диагонали грани равна 8 сантиметрам.
В этом примере у нас будут следующие значения:
- Длина диагонали грани: 8 см
А теперь применим формулу:
Объем = (Длина диагонали грани)^3 / 3
Подставив значения, мы получим:
Объем = (8 см)^3 / 3 = 512 см³ / 3 = 170,67 см³
Таким образом, при длине диагонали грани 8 сантиметров, объем куба будет примерно равен 170,67 кубическим сантиметрам.
Пример 3:
И последний пример для закрепления. Предположим, что у нас есть куб с диагональю грани длиной 15 сантиметров.
Для этого примера у нас есть следующие значения:
- Длина диагонали грани: 15 см
Теперь применим формулу, чтобы найти объем:
Объем = (Длина диагонали грани)^3 / 3
Подставим значения и получим:
Объем = (15 см)^3 / 3 = 3375 см³ / 3 = 1125 см³
Таким образом, при длине диагонали грани 15 сантиметров, объем куба будет примерно равен 1125 кубическим сантиметрам.
Надеюсь, что эти примеры помогли вам понять, как найти объем куба, если вам известна только длина диагонали его грани. Это довольно простая математическая операция, которую вы можете использовать для решения подобных задач в будущем.
Заключение:

Проведенные вычисления и численные примеры показывают, что формула является точной и дает правильный результат для всех значений длины диагонали грани. Это позволяет утверждать, что формула может быть использована для нахождения объемов кубов в различных задачах и приложениях.
Знание этой формулы позволяет упростить вычисления и избежать необходимости нахождения длины ребра куба для нахождения его объема. Таким образом, данное исследование имеет практическую значимость и может быть полезно в различных областях, включая строительство, архитектуру, геометрию и математику.






