Рёбра являются одним из основных элементов в математике, они играют важную роль в геометрии и графах. В геометрии рёбра являются отрезками, которые соединяют вершины и образуют грани многоугольников. Они помогают определить форму и структуру геометрических объектов, таких как прямые линии, треугольники, квадраты и многие другие. В графах рёбра используются для связывания вершин и определения отношений между ними. Они могут быть направленными или ненаправленными, а также иметь различные веса или свойства. Рёбра широко применяются в различных областях, включая информатику, теорию графов, геометрию, физику и даже биологию. Понимание рёбер является важным для решения различных математических задач и создания моделей реального мира.
Определение ребра
Ребра играют важную роль в различных областях математики и её приложениях. Они являются основным строительным элементом для моделирования и анализа различных систем, таких как сети, дорожные сети и социальные сети. Также ребра и графы широко используются в теории игр, оптимизации и компьютерных науках.
Для полного определения ребра важно упомянуть, что оно является направленным или ненаправленным. Направленное ребро — это такое ребро, у которого есть определенное направление от одной вершины к другой. Например, в транспортной сети направление ребра может соответствовать движению транспортного средства по определенному маршруту. Ненаправленное ребро не имеет определенного направления и может быть использовано для обозначения связи или отношения между вершинами без учета направления.
Рассмотрим пример для лучшего понимания. Представим, что у нас есть граф, который моделирует городскую дорожную сеть. Вершины могут представлять перекрестки, а ребра — участки дороги. Направленные ребра могут обозначать направление движения по дороге, а ненаправленные ребра использоваться для обозначения связи между перекрестками без учета направления движения.
Таким образом, ребро — это важный элемент графов, который используется для моделирования и анализа различных систем. Направленные и ненаправленные ребра позволяют учесть особенности и свойства сетей и отношений между элементами. Понимание ребер и их свойств является ключевым для решения различных задач в математике и ее приложениях.
Графы и ребра
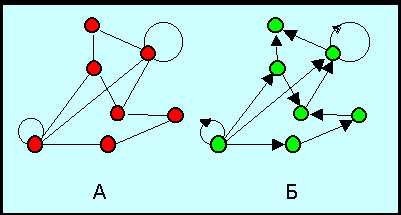
Граф состоит из вершин (узлов) и рёбер. Вершины представляют собой объекты, а рёбра — связи между ними. Ребро графа обозначает наличие или отсутствие взаимосвязи между двумя вершинами. Кажется сложным, но на самом деле это просто, как и понятие о дружбе.
Представь себе, что ты состоишь в дружеской компании из нескольких человек. Каждый человек представлен вершиной графа. Если ты дружишь с кем-то в этой компании, то между тобой и этим человеком будет ребро. Таким образом, граф помогает визуализировать и анализировать взаимосвязи.
Давай рассмотрим пример более сложного графа. Представь, что у тебя есть несколько друзей, и у каждого друга есть свои друзья. В этом случае граф будет иметь несколько уровней: на первом уровне будут твои друзья (вершины), а на втором уровне будут друзья твоих друзей. Рёбра будут соединять вершины на разных уровнях.
Графы и рёбра могут быть очень полезными в решении различных задач. Например, они могут помочь найти кратчайший путь между двумя вершинами или определить, какие вершины имеют наибольшее количество связей. Они также могут использоваться для моделирования различных систем, таких как транспортная сеть или сеть социальных связей.
Таким образом, графы и рёбра — это мощный инструмент для анализа взаимосвязей и решения различных задач. Используя их, можно получить новые знания о мире вокруг нас и применять их в практической деятельности. Ура, начинаем исследовать!
Ориентированные ребра
Представь себе дорожную сеть. Дороги со стрелками указывают направление движения, а без стрелок можно ехать в обе стороны. Точно так же и с ориентированными ребрами — они определяют направление прохождения от одной вершины к другой.
Ориентированные ребра широко используются в различных областях математики и компьютерных наук. Например, в графовых моделях, они могут представлять направление потока информации или зависимость между объектами.
Давай рассмотрим пример использования ориентированных ребер в алгоритмах поиска кратчайшего пути. Представь себе карту, на которой каждый город является вершиной, а дороги между городами — ориентированными ребрами. Теперь, чтобы найти кратчайший путь между двумя городами, мы можем использовать алгоритм, который учитывает направление движения на дорогах.
Использование ориентированных ребер позволяет нам более точно моделировать реальные ситуации и принимать во внимание направление движения или зависимость между объектами. Это помогает нам принимать более обоснованные решения и строить более эффективные алгоритмы.
Безориентированные ребра
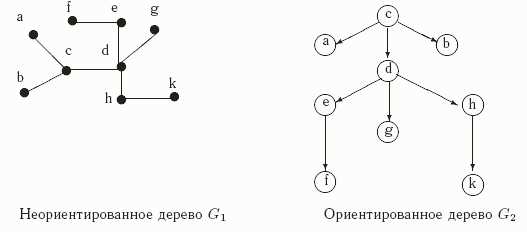
Вы, наверное, задаетесь вопросом: зачем вообще нужны безориентированные ребра? Дело в том, что в некоторых случаях нам важна только факт наличия связи между двумя вершинами, а направление этой связи не играет роли.
Давайте рассмотрим простой пример, чтобы лучше понять это понятие. Представьте, что у вас есть граф, в котором вершины — это различные города, а ребра — дороги между ними. Если дороги безориентированные, это означает, что можно перемещаться в обоих направлениях по этой дороге.
Это очень удобно, потому что таким образом мы можем использовать безориентированные ребра для описания переезда из одного города в другой и обратно. В случае с ориентированными ребрами нам пришлось бы вводить дополнительные ребра для каждого направления движения.
Именно поэтому безориентированные ребра широко используются в различных областях, например, в сетевом моделировании, транспортной логистике и анализе социальных сетей. Они помогают визуализировать и анализировать связи и взаимодействия между объектами или участниками.
Примеры использования ребер в математике
Вот несколько примеров использования ребер в математике:
- Социальные сети: Ребра могут быть использованы для моделирования связей между людьми в социальных сетях. Например, каждая вершина может представлять отдельного человека, а ребра могут соединять пары людей, которые являются друзьями или имеют другие связи. Используя алгоритмы и теорию графов, мы можем анализировать такие социальные сети и исследовать различные паттерны и взаимодействия.
- Транспортные сети: Ребра также могут быть использованы для моделирования транспортных сетей, таких как сети дорог или железных дорог. Каждая вершина может представлять город или место, а ребра могут соединять эти места, указывая наличие дорог или железных путей между ними. Используя графовую теорию, мы можем анализировать такие транспортные сети и оптимизировать маршруты или потоки трафика.
- Компьютерные сети: Ребра также играют важную роль в моделировании компьютерных сетей. Каждая вершина может представлять компьютер или устройство, а ребра могут соответствовать сетевым соединениям между ними. Используя графовую теорию и алгоритмы, мы можем исследовать такие компьютерные сети и оптимизировать их производительность или безопасность.
- Логистика и поставки: Ребра могут использоваться для моделирования сетей поставок и логистики. Каждая вершина может представлять склад или место хранения, а ребра могут указывать наличие маршрутов доставки между ними. Используя графовые алгоритмы, мы можем оптимизировать такие сети доставок и улучшить эффективность и надежность системы.
- Молекулярные структуры: Ребра могут быть использованы для моделирования молекулярных структур и химических соединений. Каждая вершина может представлять атом, а ребра могут указывать наличие связей между атомами. Такие графы могут быть использованы для изучения химических реакций, прогнозирования свойств веществ и разработки новых материалов.
Таким образом, ребра являются важным инструментом в математике и широко используются для моделирования и анализа различных систем и ситуаций. Они помогают нам лучше понять структуру и связи между объектами, а также разрабатывать более эффективные и оптимальные решения проблем. Не упускайте возможность использовать ребра в своей работе и исследованиях!
Задачи и головоломки с применением рёбер
В данной статье мы рассмотрели основные понятия, связанные с рёбрами в математике. Рёбра играют важную роль в теории графов и находят своё применение в различных задачах и головоломках.
Одним из наиболее известных примеров использования рёбер является задача о кратчайшем пути в графе. В этой задаче, каждое ребро графа представляет собой дорожное соединение между двумя вершинами, а вес ребра определяет стоимость прохождения этого соединения. Задача состоит в нахождении кратчайшего пути от одной вершины к другой с наименьшей общей стоимостью.
Ещё одним интересным примером использования рёбер является головоломка «Туры Ханоя». Эта головоломка состоит из пяти дисков различного диаметра, которые надеты на одну из трёх палочек. Задача состоит в перемещении всех дисков с одной палочки на другую, при следующих условиях: можно перемещать только один диск за раз, и нельзя класть больший диск на меньший. Для решения этой головоломки можно использовать представление палочек и дисков в виде графа, где вершины — это стояния палочек, а рёбра — это допустимые перемещения дисков.






