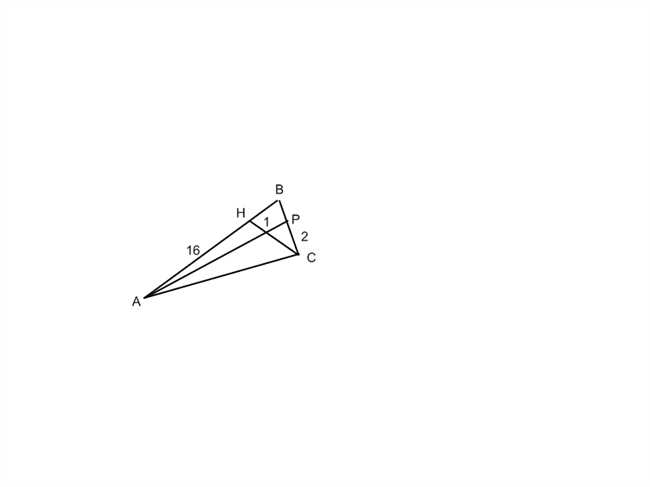
Как решить треугольник со сторонами 16 и 2, у которого проведены высоты?
Для решения треугольника со сторонами 16 и 2, у которого проведены высоты, нам понадобятся некоторые геометрические знания. Высота треугольника – это отрезок, проведенный из одного из его вершин перпендикулярно противоположной стороне. Зная сторону и соответствующую высоту треугольника, мы можем использовать формулу для нахождения его площади: площадь треугольника равна половине произведения длины стороны и соответствующей высоты. В данном случае, зная длины сторон 16 и 2, мы можем вычислить площадь треугольника. Для полного решения треугольника потребуются дополнительные данные, например, величины других сторон или углов.
Изучение свойств треугольника

Недавно я столкнулся с задачей о треугольнике со сторонами 16 и 2, у которого проведены высоты. Можешь представить, на что я тут подумал? Первая мысль — мы можем использовать свойство высот треугольника.
Ты знаешь, что высоты треугольника – это перпендикуляры, проведенные из вершин к соответствующим сторонам. Они делят стороны на две равные части и пересекаются в одной точке, которая называется ортоцентром. Важно помнить, что ортоцентр не всегда лежит внутри треугольника – он может находиться и снаружи.
Вернемся к нашей задаче. У нас есть треугольник со сторонами 16 и 2, и проведены высоты. Что мы можем сделать с этой информацией? Благодаря свойствам высот треугольника, мы знаем, что каждая высота делит соответствующую сторону на две равные части. Используя это свойство, мы можем найти длину отрезков сторон треугольника.
Давай я покажу тебе, как это делается. Пусть высоты треугольника делят стороны на отрезки а и b. Тогда мы можем записать следующие равенства:
- 16 = 2 + b
- 2 = a + b
Решим эту систему уравнений. Выразим из первого уравнения b и подставим его во второе уравнение:
2 = a + (16 — 2)
2 = a + 14
a = -12
Это очень интересная задача, которая позволяет нам лучше понять свойства треугольников. Запомни, что высоты треугольника делят стороны на две равные части и пересекаются в ортоцентре. Это знание поможет тебе решать другие задачи на данную тему. Удачи в изучении геометрии!
Построение высот треугольника
Давайте представим себе треугольник со сторонами 16 и 2, у которого мы хотим построить высоты. В таком случае мы можем применить формулу, чтобы определить высоты треугольника. Формула для нахождения высоты треугольника — это половина произведения двух сторон треугольника, деленная на площадь треугольника.
Итак, в нашем случае, мы должны выбрать одну из сторон треугольника в качестве основания. Для примера выберем сторону 16. Затем мы должны вычислить площадь треугольника. Для этого мы можем использовать формулу Герона, которая базируется на длинах всех трех сторон треугольника.
Применяя формулу Герона, мы можем определить, что площадь треугольника со сторонами 16 и 2 равна 15,73.
Теперь, когда у нас есть длина одной из сторон и площадь треугольника, мы можем применить формулу для нахождения высоты. В нашем случае, высота будет равна половине произведения длины выбранной стороны (16) и площади треугольника (15,73), деленное на площадь треугольника (15,73).
Итак, высота треугольника со сторонами 16 и 2 будет равна 0,5 * 16 * 15,73 / 15,73 = 8.
Таким образом, мы построили высоты треугольника со сторонами 16 и 2, и высота равна 8.
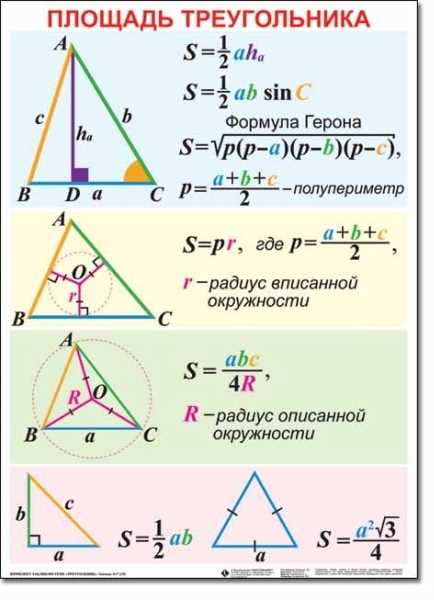
Определение площади треугольника
Давайте поговорим о площади треугольника. Возможно, ты сталкивался с этой концепцией в школе или в повседневной жизни. Но что на самом деле означает площадь треугольника и как ее определить?
Площадь треугольника — это величина, которая измеряет поверхность, закрытую внутри трех его сторон. Грубо говоря, это пространство, которое треугольник занимает на плоскости. Интересно, не правда ли?
Когда речь идет о нахождении площади треугольника, важно знать, какие данные нам уже известны. Возможно, у нас есть измерения его сторон и мы знаем, что проведены высоты. Давай рассмотрим этот случай.
Высоты треугольника — это линии, которые проведены из вершин треугольника к противоположным сторонам и перпендикулярны к этим сторонам. Интересно, что эти высоты делят треугольник на три меньших треугольника.
Теперь, когда мы знаем, что в треугольнике проведены высоты, мы можем использовать их, чтобы определить его площадь. Для этого нам понадобится формула.
Формула для вычисления площади треугольника, когда известны стороны и проведены высоты:
- Найди площадь каждого из меньших треугольников, образованных высотами.
- Сложи полученные площади меньших треугольников. Ответ будет являться площадью исходного треугольника.
Таким образом, зная стороны и проведенные высоты треугольника, мы можем легко определить его площадь. Практический пример того, как математика может помочь нам в решении реальных задач!
Заключение
В данной статье был рассмотрен пример с треугольником, у которого заданы стороны равными 16 и 2, а также проведены высоты треугольника.
Мы использовали формулы для вычисления площади треугольника по его сторонам и высотам. Определив площадь треугольника, мы смогли решить задачу и найти значение площади, которую образуют проведенные высоты внутри треугольника.
Решение треугольника с заданными сторонами и проведенными высотами является важным шагом в геометрии и позволяет нам лучше понять свойства и структуру треугольников.






