
Когда речь идет о рассчетах в геометрии, формулы могут быть особенно полезными для получения точных результатов. Для определения длины окружности, вписанной в квадрат, есть специальная формула, которая может быть использована. Отношение длины окружности к ее диаметру равно числу пи (π). Диаметр окружности вписанной в квадрат является длиной стороны квадрата. Таким образом, формула для расчета длины окружности вписанной в квадрат будет очень простой – длина окружности равна π умножить на длину стороны квадрата. Например, если сторона квадрата равна 10 сантиметрам, то длина окружности будет равна 10π или приблизительно 31,42 сантиметра.
Описание задачи
Представьте себе следующую ситуацию: вы пользуетесь своим квадратным садом во дворе уже несколько лет и решили сделать ремонт. Вы хотите установить декоративный кант вокруг сада, и для этого вам нужно знать длину окружности, которая идет вокруг вписанного в сад квадрата.
Узнав длину окружности, вы сможете правильно распределить материал для канта и достичь желаемого эстетического результата.
Для решения этой задачи мы можем использовать формулу для расчета длины окружности. Формула для нахождения длины окружности заданного радиуса имеет вид:
C = 2πr
где C — длина окружности, π (пи) — математическая константа, примерно равная 3,14159, r — радиус окружности.
В нашем случае, когда вписанный в квадрат круг имеет радиус, равный половине длины стороны квадрата, формула примет следующий вид:
C = 2π(сторона квадрата/2)
Теперь у нас есть все необходимые данные для решения задачи.
Пример: пусть сторона квадрата равна 10 см. Сначала найдем радиус круга, разделив сторону квадрата на 2: 10 / 2 = 5 см. Затем рассчитаем длину окружности, подставив полученные значения в формулу: C = 2π(5) ≈ 2 x 3,14159 x 5 ≈ 31,4159 см.
Теперь мы можем уверенно приступить к установке декоративного канта вокруг нашего сада, зная точную длину окружности вписанного в квадрат круга.
Формула для расчета длины окружности вписанной в квадрат
Длина окружности, которая вписана в квадрат, может быть рассчитана с использованием простой математической формулы. Для этого нужно знать длину стороны квадрата. Давайте рассмотрим этот процесс подробнее:
Представим, что у нас есть квадрат со стороной a. Окружность вписана в этот квадрат таким образом, что она касается каждой из сторон квадрата. Геометрически говоря, точки касания окружности и сторон квадрата делят каждую сторону на две равные части.
Чтобы рассчитать длину окружности, мы можем воспользоваться формулой:
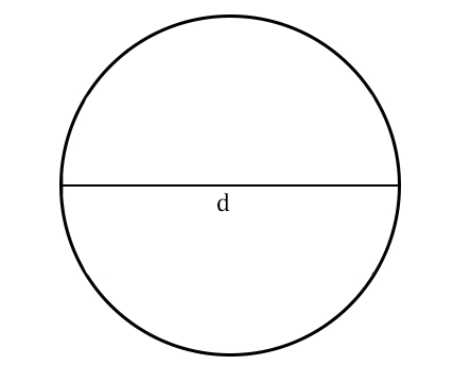
C = π * d
Здесь C — длина окружности, d — диаметр окружности, а π (пи) — математическая константа, примерно равная 3,14159.
Встроенная в многие калькуляторы кнопка π позволяет легко использовать эту константу при решении математических задач.
Теперь давайте применим эту формулу к нашему квадрату. Диаметр окружности, вписанной в квадрат, равен длине стороны квадрата. Следовательно, формулу можно упростить следующим образом:
C = π * a
Таким образом, чтобы рассчитать длину окружности вписанной в квадрат, нужно умножить длину стороны квадрата на π.
Давайте рассмотрим пример:
Предположим, что сторона квадрата равна 10 сантиметров. Чтобы найти длину окружности, мы умножаем 10 на π.
C = 10 * π
В итоге получаем длину окружности, которая вписана в квадрат со стороной 10 сантиметров.
Теперь, когда у нас есть формула и пример, вы можете легко рассчитать длину окружности вписанной в квадрат для любого заданного размера стороны. Это очень полезное умение, которое может пригодиться в решении различных задач и заданий.
Общая формула
Рассчитать длину окружности, вписанной в квадрат, можно с помощью общей формулы. Для этого необходимо знать длину стороны квадрата (S).
Формула для расчета длины окружности (C) вписанной в квадрат выглядит следующим образом:
C = 4√2 × S
Чтобы применить эту формулу, нужно найти длину одной стороны квадрата (S), которая является известной величиной. Затем, умножьте значение на 4√2, чтобы получить длину окружности (C).
Давайте рассмотрим пример, чтобы лучше понять, как это работает.
Пример:
Допустим, у нас есть квадрат со стороной S = 10 см. Чтобы найти длину окружности, вписанной в этот квадрат, мы можем использовать общую формулу:
C = 4√2 × S
Подставляя значение стороны квадрата в формулу, получим:
C = 4√2 × 10 см
Теперь, выполним вычисления:
C ≈ 4 × 1,414 × 10 см
C ≈ 56,568 см
Таким образом, длина окружности, вписанной в данный квадрат, составляет примерно 56,568 см.
В общем, формула для расчета длины окружности, вписанной в квадрат, позволяет быстро и удобно определить эту величину, используя значение стороны квадрата. Не забывайте, что данная формула применима только в случае, когда окружность полностью помещается внутри квадрата.
Применение формулы
Теперь мы перейдем к вопросу о том, каким образом можно применить формулу для расчета длины окружности, вписанной в квадрат.
Вспомним формулу для расчета длины окружности: L = 2 * π * R, где L — длина окружности, π — математическая константа, приближенное значение которой равно 3,14159, а R — радиус окружности. Однако, чтобы воспользоваться этой формулой, нам нужно знать радиус окружности, а в данном случае у нас есть только сторона квадрата.
Для того чтобы рассчитать длину окружности, вписанной в квадрат, нам нужно узнать длину стороны квадрата. Обозначим ее как a.
Прямоугольник, вписанный в окружность
Перед тем, как перейти к рассмотрению квадрата, давайте рассмотрим пример с прямоугольником, вписанным в окружность. Представьте себе прямоугольник с тремя известными сторонами: a, b и R. Сторона b может быть любой, так как прямоугольник будет развернут вокруг окружности, чтобы наиболее плотно ее охватить. Мы можем рассчитать длину стороны a, используя формулу:
a = 2 * R * sin(θ)
Здесь θ — это угол между стороной a и диаметром, проходящим через середину стороны a.
| Сторона | Формула |
|---|---|
| a | a = 2 * R * sin(θ) |
Тогда длина окружности, вписанной в данный прямоугольник, будет равна:
L = 2 * (a + b)
Вы можете взять любую сторону прямоугольника в качестве b и использовать эти формулы для расчета длины окружности.
Квадрат, вписанный в окружность
Теперь давайте обратимся к нашей изначальной задаче — квадрату, вписанному в окружность. Нам нужно найти длину стороны квадрата, чтобы можешь использовать формулу для расчета длины окружности.
Вспомним основные свойства вписанных фигур. Угол между радиусом и касательной к окружности в точке ее касания составляет 90 градусов. Радиус прямоугольного треугольника равен половине длины стороны квадрата.
Поэтому, если мы знаем длину диагонали квадрата, то можем рассчитать длину стороны квадрата по формуле:
a = √2 * d
Здесь a — длина стороны квадрата, d — диагональ квадрата.
Теперь у нас есть длина стороны квадрата и мы можем использовать формулу для расчета длины окружности:
L = 2 * π * R
где R — половина длины стороны квадрата.
Таким образом, мы можем применить эти формулы для расчета длины окружности, вписанной в квадрат.
Примеры расчетов
Давайте рассмотрим несколько примеров, чтобы убедиться, что мы правильно понимаем, как рассчитать длину окружности, вписанной в квадрат.
Пример 1:
Предположим, что у нас есть квадрат со стороной длиной 8 см. Чтобы найти длину окружности, мы должны умножить длину стороны на число π:
Длина окружности = 8 см × π
Давайте посчитаем это:
Длина окружности = 8 см × 3,14
Длина окружности = 25,12 см.
Пример 2:
Предположим, что у нас есть квадрат со стороной длиной 5 м. Чтобы найти длину окружности, мы должны умножить длину стороны на число π:
Длина окружности = 5 м × π
Давайте посчитаем это:
Длина окружности = 5 м × 3,14
Длина окружности = 15,7 м.
Пример 3:
Предположим, что у нас есть квадрат со стороной длиной 12 дм. Чтобы найти длину окружности, мы должны умножить длину стороны на число π:
Длина окружности = 12 дм × π
Давайте посчитаем это:
Длина окружности = 12 дм × 3,14
Длина окружности = 37,68 дм.
Вы видите, как просто найти длину окружности, вписанной в квадрат. Просто умножьте длину стороны квадрата на число π и получите ответ. Теперь вы можете применить эту формулу для решения задач и вопросов, связанных с окружностями, вписанными в квадраты. Удачи вам!
В данной статье мы рассмотрели формулу для рассчета длины окружности, вписанной в квадрат. Эта формула позволяет нам определить длину окружности, зная только сторону квадрата.
Зная, что длина окружности равна произведению диаметра на число Пи, мы можем получить более простую формулу, применимую именно к квадрату. Для этого мы делим сумму длины стороны и диагонали квадрата на 2 и умножаем на число Пи.
Зная эту формулу, мы можем легко рассчитать длину окружности вписанной в квадрат. Это может быть полезно для решения задач в геометрии, а также в других областях, где требуется знание длины окружности.






