
Способы нахождения sin300 и их применение в математике
1. Геометрический метод
Первый способ нахождения sin300 — использование геометрического метода. Можно представить угол 300 градусов на координатной плоскости и использовать свойства треугольника или единичной окружности для определения значения синуса. Например, можно представить 300 градусов как 60 градусов больше, чем 240 градусов, что соответствует углу, в котором синус имеет значение 0.5. Таким образом, sin300 равен sin60, что также равно 0.5.
2. Использование тригонометрических формул
Второй способ нахождения sin300 — использование тригонометрических формул. Существуют различные формулы, которые позволяют перевести углы из одной области в другую, сохраняя при этом значения тригонометрических функций. Например, можно использовать формулу sin(A + B) = sinA*cosB + cosA*sinB для расчета sin300. Здесь можно представить 300 градусов как сумму 240 градусов и 60 градусов. Зная значения синуса и косинуса для каждого из этих углов (sin240 = -0.866 и cos60 = 0.5), можно подставить в формулу и получить значение sin300.
3. Использование онлайн-инструментов

Если вы не хотите заниматься ручными вычислениями, существуют различные онлайн-инструменты, которые могут помочь вам найти значение sin300. Многие калькуляторы или сайты, посвященные математике или тригонометрии, предоставляют функции для вычисления значений тригонометрических функций для заданных углов. Просто введите значение 300 градусов и выберите функцию синуса, чтобы получить результат.
Теперь, когда вы знаете несколько способов нахождения sin300, вы можете использовать их в различных математических задачах. Например, если вам нужно вычислить значение синуса 300 градусов в дальнейших расчетах или уравнениях, вы можете использовать полученный результат для получения более точных результатов.
Математический подход
Как найти значение sin300? Это, конечно, интересный вопрос, который может показаться непростым на первый взгляд. Однако, с помощью математического подхода мы сможем легко и быстро получить ответ на этот вопрос.
Первым шагом для вычисления sin300 будет приведение угла 300 градусов к углу, лежащему в интервале [0, 360 градусов]. В нашем случае это можно сделать, вычтя из 300 градусов число 360, поскольку 300 — 360 = -60. Таким образом, мы получим эквивалентный угол, равный -60 градусов.
Вторым шагом будет использование тригонометрической окружности, чтобы определить значение sin-60. Для этого мы найдем точку на окружности, которой соответствует угол -60 градусов. Вспомним, что sin-60 равен ординате этой точки, то есть высоте, на которой она находится. Значение sin-60 можно найти, зная, что на тригонометрической окружности точка для угла -60 градусов располагается на отрицательной оси Y.
Итак, мы получили, что sin-60 = -0.866 и, следовательно, sin300 = sin(-60) = -0.866. Таким образом, мы получили окончательный и точный ответ на поставленный вопрос.
Тригонометрический круг
Тригонометрический круг имеет центр в начале координат и радиус, который равен 1. Углы измеряются против часовой стрелки от положительной оси OX. Таким образом, положительный угол поворачивает по часовой стрелке.
- Точка (1, 0) на круге соответствует углу 0 градусов, или 0 радиан, и имеет значения синуса и косинуса равные 1 и 0 соответственно.
- Точка (0, 1) на круге соответствует углу 90 градусов, или π/2 радиан, и имеет значения синуса и косинуса равные 0 и 1 соответственно.
- Точка (-1, 0) на круге соответствует углу 180 градусов, или π радиан, и имеет значения синуса и косинуса равные -1 и 0 соответственно.
- Точка (0, -1) на круге соответствует углу 270 градусов, или 3π/2 радиан, и имеет значения синуса и косинуса равные 0 и -1 соответственно.
Тригонометрический круг позволяет нам легко находить значения синуса, косинуса и тангенса любого угла на основе его расположения на круге. Для этого нужно просто выбрать нужный угол и прочитать соответствующие значения на осях.
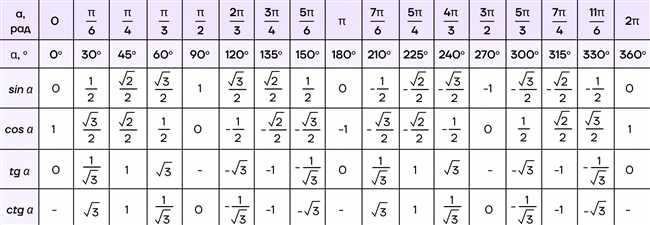
| Угол | Синус | Косинус | Тангенс |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | ∞ |
| 180° | 0 | -1 | 0 |
| 270° | -1 | 0 | -∞ |
| 360° | 0 | 1 | 0 |
Тригонометрический круг – это неотъемлемый инструмент для изучения и работы с тригонометрическими функциями. Он помогает нам легко и точно находить значения тригонометрических функций и разбираться в их связях. Умение использовать тригонометрический круг является важной составляющей математического образования и может быть применено во многих областях науки и техники.
Таблица значений sin
Так как синус является периодической функцией, то его значения могут быть представлены в виде таблицы. Ниже приводится таблица значений sin для некоторых углов:
- Угол (градусы): 0°
- Угол (радианы): 0
- Значение sin: 0
- Угол (градусы): 30°
- Угол (радианы): π/6
- Значение sin: 0.5
- Угол (градусы): 45°
- Угол (радианы): π/4
- Значение sin: √2/2 ≈ 0.707
- Угол (градусы): 60°
- Угол (радианы): π/3
- Значение sin: √3/2 ≈ 0.866
- Угол (градусы): 90°
- Угол (радианы): π/2
- Значение sin: 1
В этой таблице приведены некоторые основные значения синуса для углов в радианах и градусах от 0 до 90. Значение синуса угла больше 90° может быть вычислено с использованием тригонометрических тождеств или специальных формул.
Знание таблицы значений sin может быть полезно при решении задач, связанных с углами и тригонометрией. Оно помогает быстро находить значения синуса для известных углов и использовать их в дальнейших вычислениях.
Применение теоремы Пифагора

Эта теорема основана на простом математическом соотношении: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов.
Давайте рассмотрим пример, чтобы лучше понять, как применять теорему Пифагора. Представьте, что у вас есть прямоугольный треугольник, где один катет равен 3, а гипотенуза равна 5. Вам нужно найти длину второго катета.
Воспользуемся теоремой Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов.
В данном случае, гипотенуза равна 5, а один катет равен 3. Подставим эти значения в формулу и найдем второй катет:
- Квадрат гипотенузы равен 5 в квадрате = 25
- Квадрат первого катета равен 3 в квадрате = 9
- Сумма квадратов длин катетов равна 25 — 9 = 16
Теперь найдем квадрат длины второго катета: 16.
Чтобы найти саму длину второго катета, извлечем квадратный корень из результата:
Корень квадратный от 16 равен 4.
Таким образом, длина второго катета равна 4.
Теорема Пифагора является универсальным инструментом для решения задач, связанных с прямоугольными треугольниками. Она может быть использована в различных областях, таких как архитектура, физика и даже в ежедневной жизни.
Например, если вам нужно посчитать расстояние между двумя точками на плоскости, вы можете использовать теорему Пифагора, превратив это задание в прямоугольный треугольник, где сторонами будут разности координат точек.
Также, зная длины двух сторон треугольника, можно найти углы между ними, используя тригонометрические функции, такие как синус, косинус и тангенс.
Теперь, когда вы знакомы с теоремой Пифагора и ее применениями, вы можете использовать ее, чтобы решать разнообразные задачи и находить нужные значения в прямоугольных треугольниках.
Онлайн-инструменты для вычисления sin300
В данной статье мы рассмотрели несколько онлайн-инструментов, которые могут быть полезны при вычислении значения sin300. Среди этих инструментов можно выделить:
- Калькуляторы с тригонометрическими функциями: множество онлайн-калькуляторов позволяют вычислять значению синуса угла 300 градусов. Эти калькуляторы обеспечивают быстрый и точный результат и могут быть доступны в любое время.
- Математические приложения: некоторые приложения для смартфонов и компьютеров также предлагают возможность вычисления тригонометрических функций, включая sin300. Эти приложения обычно имеют простой и понятный интерфейс, а также способны работать без подключения к Интернету.
- Онлайн-таблицы значений тригонометрических функций: некоторые веб-сайты предлагают таблицы значений тригонометрических функций, включая sin300. Данная таблица помогает найти значение sin300 без необходимости использования специальных инструментов или приложений.
Независимо от того, какой инструмент используется, важно помнить, что значение sin300 равно -0.5. Благодаря онлайн-калькуляторам, математическим приложениям и таблицам тригонометрических функций можно легко и быстро получить это значение без долгих и сложных вычислений вручную.






