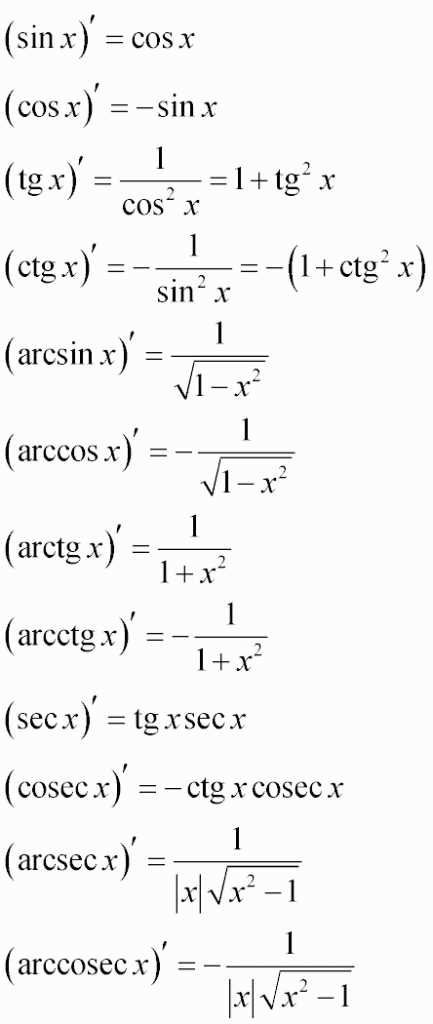
Производная от тангенса является одной из важных математических концепций, которая позволяет нам определить скорость изменения значения функции tg(x) в каждой точке ее области определения. Когда мы говорим о производной от tg(x), мы подразумеваем, что мы хотим найти тангенциальный коэффициент функции в каждой ее точке. Формула для производной tg(x) является фактически известной и определена для любого значения x, отклоняющегося от особых точек. Зная производную от tg(x), мы можем анализировать поведение функции в различных точках и использовать эту информацию для решения математических задач.
Определение и свойства функции tg(x)
Функция tg(x) имеет ряд свойств, которые могут помочь нам в понимании и использовании этой функции:
- Тангенс определен для всех действительных чисел, кроме углов, равных 90 градусов или его кратных (например, 180 градусов, 270 градусов и т. д.). В этих случаях, тангенс несущественен и не имеет определенного значения.
- Тангенс имеет периодическую природу. Это означает, что значение тангенса повторяется через определенные интервалы. Период тангенса равен π (пи).
- Функция tg(x) может принимать значения от -∞ (минус бесконечность) до +∞ (плюс бесконечность). Это означает, что тангенс может быть положительным, отрицательным или равным нулю.
- В первой четверти координатной плоскости (0° < x < 90°), тангенс положителен.
- Во второй четверти (90° < x < 180°), тангенс отрицателен.
- В третьей четверти (180° < x < 270°), тангенс снова положителен.
- В четвертой четверти (270° < x < 360°), тангенс вновь отрицателен.
Тангенс является важной функцией в тригонометрии и имеет множество приложений в различных областях, таких как физика, инженерия и компьютерная графика. Знание свойств тангенса поможет нам понять и использовать его в аналитических и прикладных задачах.
Доказательство формулы для производной от tg(x).
Чтобы понять, как доказать формулу для производной от tg(x), нам нужно вернуться к определению тангенса.
Тангенс угла x можно определить как отношение синуса к косинусу этого угла:
tg(x) = sin(x) / cos(x)
Теперь нам нужно найти производную этой функции. Для этого мы воспользуемся правилом дифференцирования частного функций.
Для начала найдем производные от синуса и косинуса. Выразим sin(x) и cos(x) с помощью экспоненциального представления:
- sin(x) = (e^(ix) — e^(-ix)) / (2i)
- cos(x) = (e^(ix) + e^(-ix)) / 2
Здесь мы использовали формулу Эйлера, которая связывает экспоненту и синус-косинусные функции.
Затем найдем производные от синуса и косинуса:
- d/dx sin(x) = (ie^(ix) + i e^(-ix)) / 2
- d/dx cos(x) = (ie^(ix) — i e^(-ix)) / 2
Теперь давайте найдем производную от tg(x) по определению:
d/dx tg(x) = (d/dx sin(x) * cos(x) — sin(x) * d/dx cos(x)) / cos^2(x)
Подставим значения производных sin(x) и cos(x):
d/dx tg(x) = ((ie^(ix) + i e^(-ix)) / 2 * (e^(ix) + e^(-ix)) / 2 — (e^(ix) — e^(-ix)) / (2i) * (ie^(ix) — i e^(-ix)) / 2) / ((e^(ix) + e^(-ix)) / 2)^2
Упростим выражение и перемножим числители:
d/dx tg(x) = (ie^(2ix) + ie^(-2ix) + e^(ix) + e^(-ix) — e^(ix) + e^(-ix) — ie^(2ix) + ie^(-2ix)) / (4i * (e^(ix) + e^(-ix))^2)
Теперь упростим числитель:
d/dx tg(x) = (2i * (e^(-2ix) — e^(2ix))) / (4i * (e^(ix) + e^(-ix))^2)
Сокращаем на i в числителе и знаменателе:
d/dx tg(x) = (e^(-2ix) — e^(2ix)) / (e^(ix) + e^(-ix))^2
Далее используем формулу Эйлера для выражения экспоненты через тригонометрические функции:
d/dx tg(x) = (cos(2x) — sin(2x)i — (cos(2x) + sin(2x)i)) / (cos(x) + sin(x)i + cos(x) — sin(x)i)^2
Теперь упростим выражение:
d/dx tg(x) = (cos(2x) — sin(2x)i — cos(2x) — sin(2x)i) / (2cos(x))^2
Получаем:
d/dx tg(x) = -2sin(2x) / (2cos(x))^2
Дальше упростим выражение:
d/dx tg(x) = -sin(2x) / cos^2(x)
Таким образом, мы доказали формулу для производной от tg(x):
d/dx tg(x) = -sin(2x) / cos^2(x)
Именно этим математическим доказательством мы доказали формулу для нахождения производной от тангенса.
Примеры нахождения производной от tg(x)
Пример 1: Найдем производную от tg(x).
Используя определение производной, мы получаем:
f'(x) = lim(h→0) [tg(x + h) — tg(x)] / h
Заметим, что при подходе разности x + h — x к нулю получается просто h. Поэтому имеем:
f'(x) = lim(h→0) [tg(x + h) — tg(x)] / h
Раскрываем тангенс суммы в числителе:
f'(x) = lim(h→0) [(sin(x + h) / cos(x + h)) — (sin(x) / cos(x))] / h
Далее преобразуем числитель:
f'(x) = lim(h→0) [(sin(x)cos(h) + cos(x)sin(h)) / cos(x + h)] — (sin(x) / cos(x))] / h
Упрощаем выражение:
f'(x) = lim(h→0) [(sin(x)cos(h) + cos(x)sin(h) — sin(x)cos(x) — cos(x)sin(h)) / cos(x)cos(h))] / h
Сокращаем слагаемые синуса и косинуса:
f'(x) = lim(h→0) [0 / cos(x)cos(h))] / h
Получаем 0 в числителе и убираем зависимость от h в знаменателе:
f'(x) = 0
Таким образом, производная от tg(x) равна нулю. Это означает, что функция tg(x) является константой и не изменяется со временем.
Пример 2: Найдем производную от tg(5x).
Для нахождения производной от функции, в которой переменная умножается на число, мы можем использовать правило дифференцирования произведения.
Имеем:
f(x) = tg(5x)
Применяем правило:
f'(x) = 5 * tg'(5x)
Теперь остается только найти производную от tg(x), как мы делали в первом примере:
f'(x) = 5 * 0
f'(x) = 0
Таким образом, производная от tg(5x) также равна нулю.
- Производная от tg(x) равна нулю.
- Производная от tg(5x) также равна нулю.
- Функция tg(x) является константой, которая не меняется со временем.
Надеюсь, эти примеры помогли вам лучше понять нахождение производной от tg(x) и ее значения в различных случаях.
Применение производной от tg(x) в задачах математического анализа
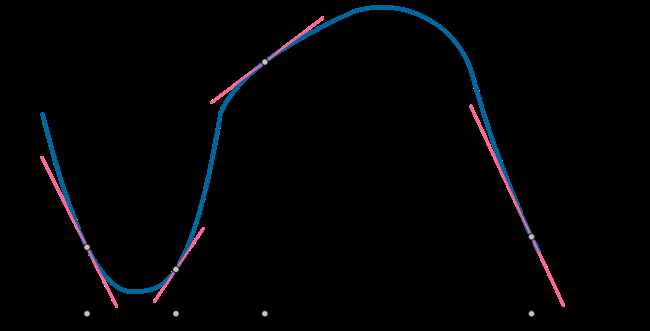
Одним из основных применений производной от tg(x) является анализ поведения функций и определение точек, в которых функция принимает экстремальные значения. При помощи производной можно выяснить, где функция имеет максимум или минимум, а также определить точки, в которых функция возрастает или убывает.
Кроме того, производная от tg(x) может быть использована для нахождения касательной линии к графику функции в заданной точке. Касательная линия имеет наклон, который равен значению производной в этой точке. Используя эту информацию, можно изучить локальное поведение функции в окрестности заданной точки.
Другой важной областью применения производной от tg(x) является решение задач на определение скорости изменения величин. Производная может помочь определить мгновенную скорость изменения функции в заданной точке. Это полезно при решении задач, связанных с физикой, экономикой или другими областями, в которых требуется изучение скорости изменения величин.
В целом, производная от tg(x) является мощным инструментом в математическом анализе, который может быть использован для решения различных задач. Она позволяет более глубоко изучать поведение функций, а также даёт возможность анализировать их свойства и находить полезную информацию о них.






