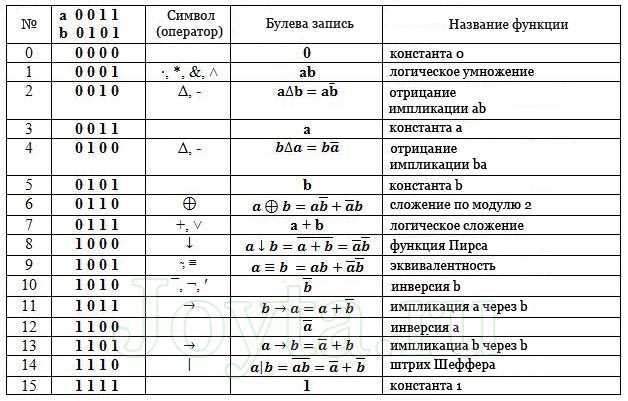
Значение символа U в алгебре: расшифровка и примеры
В алгебре символ U играет важную роль и имеет множество применений. Он обычно используется для обозначения множества всех элементов, которые удовлетворяют определенному условию. Буква U происходит от английского слова «union» (объединение) и обозначает объединение множеств.
Например, если имеются два множества A = {1, 2, 3} и B = {3, 4, 5}, то их объединение обозначается как A U B и представляет собой множество {1, 2, 3, 4, 5}, которое включает все элементы из обоих исходных множеств.
Символ U также может использоваться для обозначения объединения более чем двух множеств. Например, если имеются множества A = {1, 2}, B = {2, 3} и C = {3, 4}, то их объединение будет обозначаться как A U B U C и представлять собой множество {1, 2, 3, 4}.
Таким образом, символ U является важным инструментом в алгебре и позволяет объединять множества, а также выполнять другие операции с ними.
Расшифровка символа U в алгебре
Символ U в алгебре представляет собой обозначение для множества, которое содержит все элементы из двух или более множеств. Он широко используется в различных областях математики и имеет важное значение в логике, теории множеств, теории вероятности и других дисциплинах.
Когда мы видим символ U между двумя множествами, это означает объединение этих множеств. То есть, символ U позволяет нам объединить все элементы из этих множеств в одно общее множество.
Давайте рассмотрим пример: пусть есть два множества — A = {1, 2, 3} и B = {3, 4, 5}. Если мы применим операцию объединения с использованием символа U, то получим следующее множество: A U B = {1, 2, 3, 4, 5}. Таким образом, все элементы из множества A и множества B объединены в одно общее множество.
Символ U также используется для объединения более чем двух множеств. Например, пусть у нас есть множество A = {1, 2} и множество B = {3, 4}, и множество C = {5, 6}. Мы можем объединить все эти множества с помощью символа U следующим образом: A U B U C = {1, 2, 3, 4, 5, 6}. В результате получается множество, содержащее все элементы из множеств A, B и C.
Символ U также может использоваться для объединения бесконечных множеств. Например, пусть A — множество четных чисел {2, 4, 6, …} и B — множество нечетных чисел {1, 3, 5, …}. Тогда объединение A U B содержит все натуральные числа, так как каждое натуральное число является либо четным, либо нечетным.
Итак, символ U в алгебре представляет собой мощное инструмент для объединения множеств и создания общих наборов данных. Он позволяет нам работать с различными множествами и выполнять различные операции над ними.
Значение символа U в алгебре
В алгебре символ U используется для обозначения множества. При этом, U означает «универсальное множество» или «универсум». Универсум представляет собой область, которую мы изучаем или рассматриваем в определенном контексте.
Универсальное множество включает в себя все элементы, которые мы рассматриваем. Например, если мы изучаем множество всех целых чисел, то U будет обозначать именно это множество всех целых чисел.
Символ U также используется в контексте операций над множествами, таких как объединение, пересечение и разность. Например, если A и B — два множества, то объединение A и B обозначается как A ∪ B, где символ ∪ обозначает объединение. Таким образом, U используется вместе с другими символами для обозначения конкретных операций над множествами.
Пример использования символа U в алгебре:
- Пусть U — множество всех студентов в университете;
- Пусть A — множество студентов, занимающихся спортом;
- Пусть B — множество студентов, изучающих иностранные языки.
Тогда объединение множеств A и B будет обозначаться как A ∪ B, а пересечение множеств A и B — A ∩ B. В данном контексте символ U представляет собой множество всех студентов в университете, которое является универсальным множеством для рассматриваемых множеств A и B.
Таким образом, символ U в алгебре имеет значение «универсальное множество» и используется для обозначения множеств и операций над ними.
Применение символа U в алгебре
Символ U широко используется в алгебре и имеет несколько значений и применений. В зависимости от контекста, символ U может означать объединение множеств, множество всех элементов удовлетворяющих некоторому условию, множество алгебраических нимов или некоторую операцию на множестве. Рассмотрим каждое из этих значений подробнее.
1. Объединение множеств
Когда символ U используется для обозначения объединения множеств, он обозначает операцию, которая объединяет все элементы двух или более множеств в одно множество. Например, если у нас есть множество A = {1, 2, 3} и множество B = {3, 4, 5}, то объединение этих двух множеств будет обозначаться как A U B и будет содержать все элементы из обоих множеств: {1, 2, 3, 4, 5}.
2. Множество всех элементов с определенным свойством
Символ U также может использоваться для обозначения множества всех элементов, удовлетворяющих некоторому условию или свойству. Например, пусть у нас есть множество всех целых чисел, и мы хотим найти множество всех четных чисел. Мы можем обозначить это множество как E = x делится на 2, где символ U означает «элемент из множества» («элемент принадлежит множеству») и символ ∈ означает «принадлежит». Таким образом, E будет содержать все четные числа: {2, 4, 6, …}.
3. Множество алгебраических нимов
В алгебре символ U может использоваться для обозначения множества алгебраических нимов. Алгебраические нимы – это математический объект, который может представлять собой число, переменную или выражение. Символ U обычно используется в контексте алгебры Буля, где он обозначает множество всех возможных значений логических переменных. Например, если у нас есть две логические переменные A и B, то множество всех возможных комбинаций значений этих переменных можно обозначить как U = {0, 1}.
Примеры использования символа U в алгебре
Символ U в алгебре имеет различные значения и применения, которые могут быть полезными в решении алгебраических задач. Вот несколько примеров использования символа U:
1. Объединение множеств
В алгебре символ U используется для обозначения операции объединения множеств. Например, если у нас есть множество A = {1, 2, 3} и множество B = {3, 4, 5}, то их объединение обозначается как A U B и представляет собой новое множество, содержащее все элементы из множества A и B без повторений. Таким образом, A U B = {1, 2, 3, 4, 5}.
2. Универсальное множество
В алгебре символ U также используется для обозначения универсального множества, которое представляет собой множество, содержащее все возможные элементы, которые могут быть использованы в рассматриваемой алгебраической системе. Например, если рассматривается множество всех натуральных чисел, то универсальное множество будет обозначаться как U = {1, 2, 3, …}.
3. Множество всех точек
Еще одним примером использования символа U в алгебре может быть обозначение множества всех возможных точек на плоскости или в пространстве. Например, если мы рассматриваем множество всех точек на плоскости, то это множество может быть обозначено как U = (x, y) .
4. Импликация
Символ U также может использоваться для обозначения операции импликации в алгебре. Импликация является логической операцией, которая устанавливает, что если одно высказывание истинно, то другое высказывание тоже истинно. Например, выражение «P U Q» может обозначать, что высказывание P влечет высказывание Q, то есть если P истинно, то Q также должно быть истинно.
5. Множество узлов в графах
В теории графов символ U может использоваться для обозначения множества узлов в графе. Граф — это набор узлов, соединенных ребрами. Если у нас есть граф G с набором узлов U, то мы можем записать его в виде G = (U, E), где E — множество ребер графа.
В конце концов, символ U имеет различные значения и применения в алгебре, позволяя нам работать с множествами, логическими операциями, графами и другими математическими структурами. Вы можете использовать эти примеры в своих решениях алгебраических задач и расширить свои знания в алгебре. Подумайте о том, где и как вы можете применить символ U!
Сочетание символов U и других операций в алгебре
Когда символ U используется в контексте двух множеств, например A и B, он показывает, что нужно объединить все элементы из A и B, исключая повторяющиеся элементы. Например, если A = {1, 2, 3} и B = {3, 4, 5}, то A U B будет равно {1, 2, 3, 4, 5}.
Символ U может также сочетаться с другими операциями, такими как «пересечение» (обозначается символом ∩) и «разность» (обозначается символом -). Например, для множеств A = {1, 2, 3} и B = {3, 4, 5}, A U B ∩ B означает, что нужно сначала объединить множества A и B, а затем найти элементы, которые присутствуют и в A U B, и в B. В данном случае результатом будет множество {3}, потому что это единственный элемент, присутствующий и в A U B, и в B.
Символ U может использоваться также в контексте более сложных алгебраических выражений, включающих операции объединения, пересечения и разности. Например, если у нас есть множества A = {1, 2, 3}, B = {3, 4, 5} и C = {2, 3, 6}, то выражение (A U B) ∩ C — B означает, что нужно сперва объединить множества A и B, затем найти общие элементы с множеством C, а затем вычесть элементы множества B. Результатом будет множество {2}, так как только число 2 присутствует и в (A U B) ∩ C, и в B.
Таким образом, сочетание символов U и других операций в алгебре позволяет выполнять различные операции над множествами, находить пересечения, объединения и разности элементов, а также строить более сложные выражения. Эти операции часто применяются в математике, логике, статистике, программировании и других областях, где требуется работа с множествами элементов.
Заключение
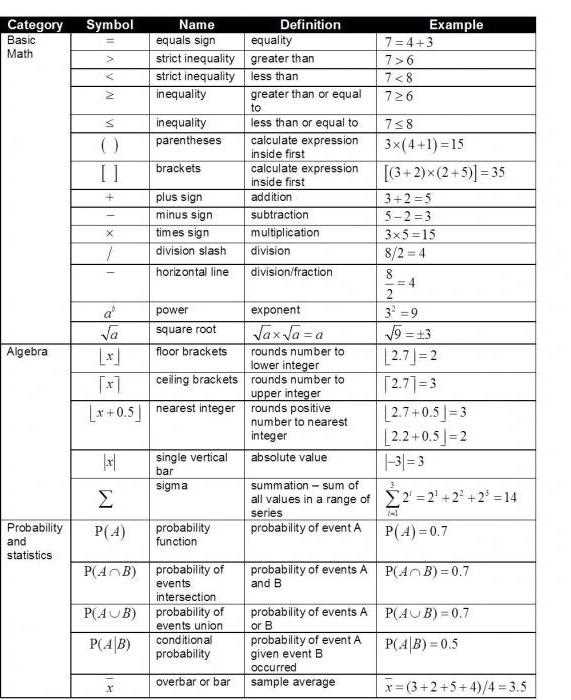
Символ U играет важную роль в алгебре и имеет практическое применение в решении различных задач. Он используется для обозначения множества значений переменных или функций в уравнениях и неравенствах.
Применение символа U особенно полезно при работе с совокупностями или объединениями множеств. Он позволяет наглядно и компактно записывать все возможные значения, которые могут принимать переменные или функции в заданных условиях.
Примеры использования символа U можно найти в различных областях: от математики и программирования до физики и экономики. Умение правильно интерпретировать и использовать символ U может значительно упростить решение задач и повысить точность и наглядность представления результатов.
Итак, символ U является мощным инструментом, который помогает математикам и другим специалистам в анализе и решении задач. Его практическое применение демонстрирует его значимость и необходимость в современном мире.
