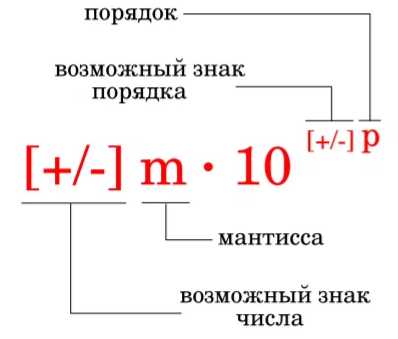
Знак «следовательно» в алгебре
Например, если есть утверждение «Если два числа равны, то их произведение также будет равно», можно записать это выражение следующим образом: «a = b, следовательно, a * c = b * c». В этом случае знак «следовательно» указывает на логическую связь между равенством двух чисел и равенством их произведений.
Когда используется знак «следовательно» в алгебре, очень важно понимать, что он показывает только логическую связь между двумя выражениями или предложениями. Этот знак не указывает на причину или обоснование этой связи, а просто предоставляет информацию о логическом следствии.
Определение и назначение знака «следовательно»
Знак «следовательно» имеет следующее назначение:
- Показывает, что из одной или нескольких предпосылок можно сделать определенное заключение.
- Выражает отношение логической импликации, где предпосылка является условием, а следствие — результатом.
Использование знака «следовательно» позволяет создать логическую связь между условием и его следствием, что помогает строить более четкие и последовательные математические аргументы.
Обозначение знака «следовательно»
Знак «следовательно» в алгебре обозначается символом «⇒», который имеет следующий вид:
⇒
Этот символ используется для обозначения отношения следования или импликации между двумя высказываниями или утверждениями. Он говорит о том, что если первое высказывание верно, то второе высказывание также должно быть верным.
Например, если у нас есть высказывание «Если сегодня идет дождь, то улицы мокрые», мы можем записать его с использованием знака «следовательно» следующим образом:
Дождь ⇒ Улицы мокрые
Такая запись говорит о том, что если сегодня идет дождь, то это приведет к тому, что улицы станут мокрыми. Знак «⇒» позволяет нам установить связь между двумя высказываниями и объяснить отношение причины и следствия.
Использование знака «следовательно» помогает нам лучше понять логические связи между утверждениями и рассуждать более последовательно. Он позволяет нам строить аргументацию и доказывать различные теоремы и утверждения в алгебре и математике.
Примеры использования знака «следовательно»
Вот несколько примеров использования знака «следовательно» в различных контекстах:
1. Алгебра:
В алгебре знак «следовательно» используется для обозначения логического условия.
- Если a > b, то a + c > b + c. (a > b) → (a + c > b + c)
- Если x = 2, то x^2 = 4. (x = 2) → (x^2 = 4)
- Если a = b и b = c, то a = c. (a = b) ∧ (b = c) → (a = c)
2. Логика:
В логике знак «следовательно» используется для обозначения логического следствия.
- Если сегодня понедельник, следовательно, завтра будет вторник. (сегодня понедельник) → (завтра вторник)
- Если все люди смертны, то Сократ также смертен. (все люди смертны) → (Сократ смертен)
- Если истина, что «A и B», то истина, что «A». (A и B) → (A)
3. Математические доказательства:
В математических доказательствах знак «следовательно» используется для указания логической связи между предыдущими утверждениями и следующим утверждением.
- Пусть a и b — произвольные целые числа. Если a четное и b четное, то a + b четное. (предположение) Если a четное и b четное, (доказательство) то a + b четное.
- Если x^2 = 25, то x = 5 или x = -5. (предположение) Если x^2 = 25, (доказательство) то x = 5 или x = -5.
Знание и понимание использования знака «следовательно» в алгебре и логике позволяет лучше анализировать причинно-следственные отношения и составлять логические рассуждения. Также, загляните в другие области математики и науки, чтобы увидеть, где еще можно использовать знак «следовательно».
Правило записи знака «следовательно» в алгебре очень важно для понимания и применения математических обозначений и формул. Знак «следовательно» выражает логическую связь между предпосылками и заключением.
Правило записи знака «следовательно» помогает студентам и ученым ясно выражать свои мысли и доказательства в математических выражениях. Оно также помогает логически анализировать и проверять математические уравнения и утверждения.
Использование правила записи знака «следовательно» позволяет проводить более точные и последовательные математические выкладки и доказательства. В алгебре это является основой для построения сложных математических моделей и решения сложных проблем.






