Как построить высоту, медиану и биссектрису треугольника с помощью циркуля — подробное руководство
Добро пожаловать! В этом подробном руководстве я расскажу тебе о том, как построить высоту, медиану и биссектрису треугольника с помощью циркуля. Эти построения являются важными элементами геометрии и могут быть полезны в различных математических и геометрических задачах. Для каждого из построений я раскрою технику и приведу примеры, чтобы помочь тебе лучше понять их суть. Будем использовать простые и понятные шаги, поэтому даже если ты не сильно знаком с геометрией, смело к нам присоединяйся! Погрузимся в мир геометрии и начнем строить!
Как построить высоту треугольника с помощью циркуля — подробное руководство
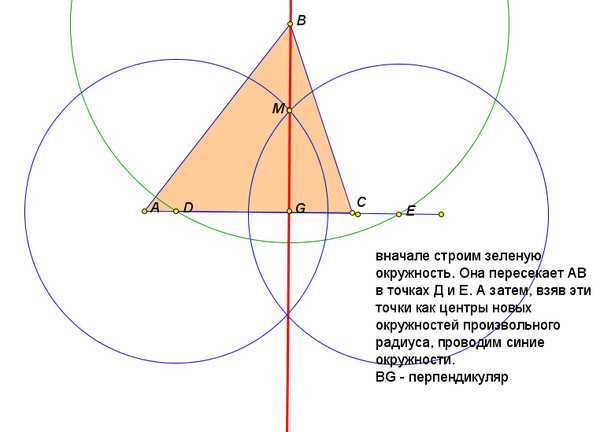
Для начала нам понадобится рисунок треугольника, на котором мы будем строить высоту. Представь, что у нас есть треугольник ABC, и мы хотим построить высоту, выходящую из вершины A.
Давай начнем с построения окружности с центром в точке A и проходящей через точки B и C. Это можно сделать с помощью циркуля. Установи одну из ног циркуля в точку A и нарисуй дугу, которая пересечет линию AB и линию AC. Эта дуга должна быть достаточно длинной, чтобы пересечь обе стороны треугольника.
Теперь возьмем циркуль и установим его ногу в точку B на стороне AC. Рисуем дугу, которая пересекает линию AB и линию BC. Аналогично, установим циркуль в точку C на стороне AB и нарисуем дугу, пересекающую линию AC и линию BC.
Теперь наша задача – найти точку пересечения дуг между линиями AB и BC. Обычно эта точка обозначается как D. Чтобы найти точку D, поставь ногу циркуля в точку A, нарисуй дугу, пересекающую первую дугу между линиями AB и AC, и продолжи дугу до ее пересечения с линией BC. Это и будет точка D – точка пересечения дуг.
Теперь, когда у нас есть точка D, мы можем построить высоту треугольника из вершины A. Для этого просто нарисуй линию AD, которая проходит через точку D и перпендикулярна к основанию треугольника BC.
Таким образом, мы успешно построили высоту треугольника ABC с помощью циркуля. Давай попрактикуемся и попробуем построить высоту других треугольников!
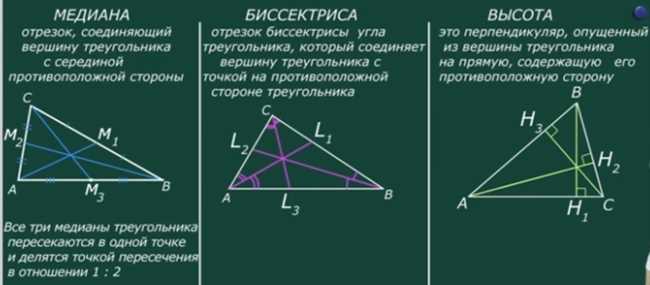
Определение высоты треугольника
Высота разделяет основание треугольника на две равные части, при этом сама высота является высотой к обоим этих частям. Кроме того, в треугольнике можно провести три высоты, и они могут пересекаться в одной точке, которая называется ортоцентром. Ортоцентр может лежать на внутренней части треугольника, на его сторонах или даже вне треугольника. Если треугольник прямоугольный, ортоцентр будет совпадать с вершиной прямого угла.
Высота треугольника играет важную роль в его геометрии и имеет множество свойств и применений. Она используется для вычисления площади треугольника по формуле: половина произведения основания треугольника и его высоты. Высота также помогает определить центр окружности, вписанной в треугольник.
Зная все это, вы можете использовать циркуль и линейку, чтобы построить высоту треугольника и изучить его свойства и особенности. Не бойтесь экспериментировать и задавать вопросы — это поможет вам лучше понять геометрию и расширит ваше понимание математических концепций.
Построение высоты треугольника с помощью циркуля
Перед тем как начать построение, убедитесь, что у вас есть лист бумаги, карандаш и циркуль. Также вам понадобится треугольник, у которого известны длины сторон или координаты вершин. Если у вас есть только стороны треугольника, вы можете использовать теорему Пифагора или теорему косинусов для определения длин сторон.
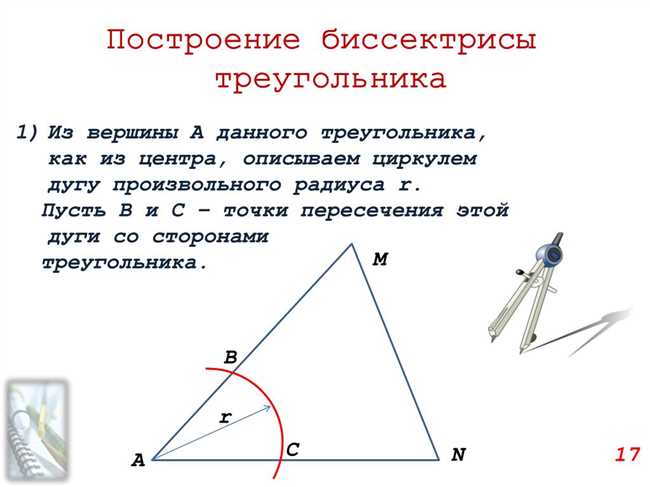
- Выберите любую вершину треугольника и назовите ее «A».
- Возьмите циркуль и на отметке 0 поставьте одну ногу циркуля на вершину «A».
- Поставьте другую ногу циркуля на противоположную сторону треугольника.
- Теперь, не меняя расстояния между ногами циркуля, поверните его, чтобы переместить другую ногу на одну из точек пересечения стороны треугольника с окружностью циркуля.
- Из точки пересечения окружности с стороной треугольника проведите прямую линию, идущую через вершину «A». Это будет высота треугольника.
Вы можете повторить этот процесс для каждой вершины треугольника, чтобы построить высоты, и они все пересекутся в одной точке, называемой ортоцентром треугольника.
Важно помнить, что для построения высоты треугольника с помощью циркуля необходимо, чтобы сторона треугольника пересекала окружность циркуля в двух точках. Если сторона треугольника параллельна окружности, такое построение высоты будет невозможным.
Итак, теперь вы знаете, как построить высоту треугольника с помощью циркуля. Этот метод может быть полезным при решении задач с треугольниками или при построении геометрических конструкций. Так что возьмите свой циркуль и начните строить!
Практическое применение высоты треугольника
Одно из наиболее распространенных практических применений высоты треугольника — определение площади треугольника. При известной высоте треугольника и его основании, площадь треугольника может быть вычислена по формуле: S = 1/2 * a * h, где S — площадь, a — основание, h — высота.
Кроме того, высоты треугольников используются в архитектуре и строительстве для определения угла подъема или наклона стен, решения задач по местоположению точек при разметке земельного участка и даже для расчета объема склонов или косогоров при строительстве дорожных трасс.
Высоты треугольников также используются в геодезии для определения высоты точек на местности. Открывая новые возможности в картографии и измерениях, высоты треугольников обеспечивают точные данные для создания 2D и 3D моделей земной поверхности.
Таким образом, практическое применение высоты треугольника включает в себя различные области, от строительства до геодезии и предоставляет нам полезные инструменты для измерения и анализа данных. Понимание и применение высот треугольника может быть полезным для людей, работающих в различных профессиональных областях и обеспечивает точность в решении конкретных задач.






