Почему медиана треугольника делит пополам угол, из которого проведена? Объясняем причины и механизм!.

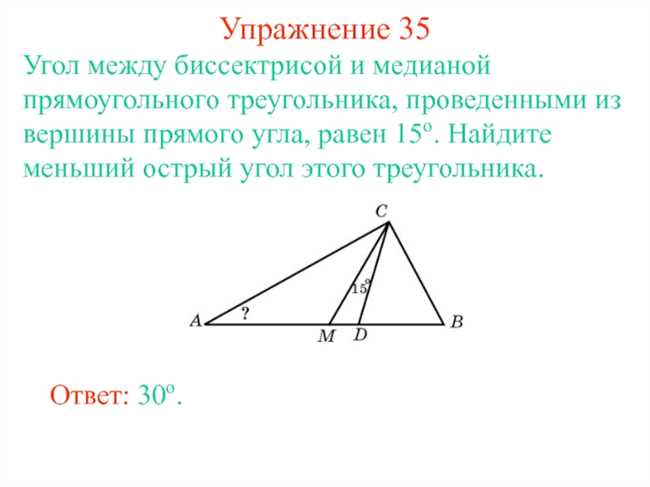
Одной из интересных математических особенностей треугольника является то, что медиана, проведенная из вершины, делит пополам угол, из которого она проведена. То есть, если мы берем произвольный треугольник и проводим медиану из одной из его вершин, она точно поделит угол, из которого проведена, пополам. Эта особенность может быть объяснена геометрически и аналитически. Геометрически, медиана треугольника является линией, соединяющей вершину с серединой противоположной стороны. Аналитически, можно использовать координаты вершин треугольника и показать, что точка пересечения медианы и угла действительно делит его пополам. Эта математическая особенность имеет много практических приложений и используется в различных областях, таких как геометрия, строительство и дизайн.

Заголовок 1: Определение медианы треугольника

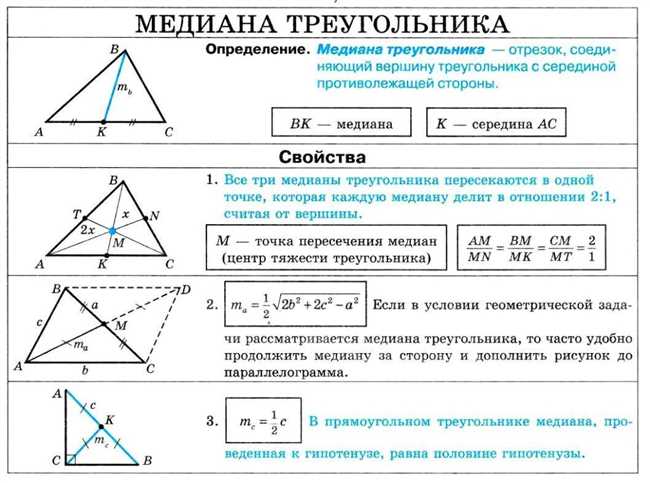
Медиана имеет несколько важных свойств и определений. Во-первых, медиана всегда делит сторону треугольника пополам. Например, в треугольнике ABC медиана BD делит сторону AC пополам. Это свойство можно легко проверить, измерив длину сторон треугольника и длину отрезков, на которые медиана делит сторону.

Во-вторых, медиана треугольника также имеет свойство делить угол, из которого она проведена, пополам. Вершина треугольника, точка, в которой все три стороны пересекаются, называется центром масс треугольника. Медианы треугольника пересекаются в одной точке, которая является центром масс. Это означает, что любая медиана делит угол, из которого она проведена, пополам.

Можно представить медиану треугольника как ось баланса, которая уравновешивает вес треугольника в каждой его части. Таким образом, медиана является важным элементом треугольника, который определяет его геометрические свойства и отношения между сторонами и углами.

Что такое медиана треугольника

Медианы треугольника пересекаются в одной точке, которая называется центром масс треугольника или центроидом. Центроид делит каждую медиану в отношении 2:1, то есть отношение расстояния от вершины до центроида к расстоянию от центроида до середины противоположной стороны равно 2:1.

Таким образом, медиана треугольника делит пополам сторону треугольника, с которой она проведена. Более того, медиана также делит пополам угол, из которого она проведена. Это можно легко увидеть, если представить, что каждая сторона треугольника — это рука весов, а медиана — шарнир, который соединяет руки. В этом случае, медиана играет роль опоры, которая делит вес на две части в равной пропорции.

Свойства медианы треугольника

1. Медиана делит площадь треугольника пополам

Одно из самых важных свойств медианы — она делит площадь треугольника пополам. Если мы проведем все три медианы треугольника, они встретятся в одной точке, которая называется центром масс (или центроидом) треугольника. В этой точке площадь треугольника равна сумме площадей трех меньших треугольников, образованных медианами.

2. Медиана является лучшей линией симметрии

Медианы треугольника являются идеальными линиями симметрии. Если мы проведем медиану из одного угла треугольника, она разделит противолежащую сторону пополам. Таким образом, каждый отрезок, соединяющий угол треугольника с серединой противолежащей стороны, будет иметь одинаковую длину.

3. Медиана делит угол пополам

Как вы уже отметили, медиана треугольника делит пополам противолежащий ей угол. Это свойство следует из симметрии треугольника. Если мы проведем две медианы из двух углов, они пересекутся на третьей медиане. Это означает, что каждый из четырех углов, образованных медианами, будет иметь одинаковую величину. В итоге, медиана делит угол пополам.

4. Медианы — глаза треугольника

Согласно одной определенной метафоре, медианы треугольника могут быть идентифицированы как «глаза» треугольника. Когда мы смотрим на треугольник через медианы, они показывают нам его цвет и форму. Медианы также позволяют нам определить технические характеристики треугольника, такие как центроид и длины сторон.

Таким образом, свойства медианы треугольника делают ее одним из наиболее интересных и полезных элементов в геометрии. Она не только разделяет треугольник пополам, но и обладает множеством других качеств, которые помогают нам понять и изучить треугольники.

Первое свойство медианы треугольника

Одним из важных свойств медианы является то, что она делит угол, из которого проведена, пополам. То есть, если мы проведем линию, соединяющую одну из вершин треугольника с серединой противоположной стороны, эта линия будет разделять этот угол на две равные части. Но почему это так? Давайте рассмотрим это более детально:

Возьмем треугольник с вершинами A, B и C. Проведем медиану из вершины A и обозначим точку пересечения с противоположной стороной как D. Теперь посмотрим на угол BAC и угол CAD.

Угол BAC – это угол между сторонами AB и AC. Угол CAD – это угол между сторонами CD и AC. Так как медиана AD проходит через середину стороны BC, то сторона CD будет равна стороне BD (ведь середина отрезка делит его пополам). А значит, треугольник ACD будет равнобедренным треугольником.

Теперь, так как у прямоугольного треугольника ACD (угол CAD — это прямой угол) боковые стороны равны, то и его углы равны. Значит, угол CAD разделяется медианой AD пополам.

Взаимосвязь медианы и углов треугольника

Для лучшего понимания этого свойства, давайте рассмотрим треугольник ABC, где M — середина стороны BC. Проведем медиану AM. Теперь, давайте проведем высоты треугольника из вершин B и C, обозначим их как BH и CK соответственно.

Теперь давайте рассмотрим треугольники AMB и AMC. Они имеют общую сторону AM и равны по построению. Кроме того, у них равные стороны BM и CM, так как это медианы треугольника ABC. Следовательно, данные треугольники равны по двум сторонам и по общему углу. Поэтому AMB и AMC являются равногранными треугольниками.

Таким образом, в треугольнике ABC угол BAC делится медианой AM пополам. Это свойство может быть доказано и для других углов треугольника, используя аналогичное рассуждение.

Взаимосвязь медианы и углов треугольника очень важна и находит широкое применение в геометрии. Проявляется она, например, в задачах на построение треугольника по заданным условиям, а также в доказательствах других геометрических теорем.

Примеры использования медианы и ее связь с углами треугольника

• Построение треугольника по заданным условиям. Зная длины двух сторон треугольника и угол между ними, мы можем использовать медиану, чтобы построить треугольник
• Доказательство теорем. Например, используя свойство медианы и углов треугольника, можно доказать, что сумма углов треугольника равна 180 градусов

Таким образом, медиана треугольника действительно делит пополам угол, из которого проведена, и это свойство является одним из ключевых в геометрии.

Как медиана делит угол, из которого проведена

Представим, что у нас есть треугольник ABC, в котором медиана BD проведена из вершины B. Давайте обратим внимание, что угол ABD и угол CBD являются вертикальными углами. Вертикальные углы равны и равны между собой. Поэтому, угол ABD и угол CBD равны.

В то же время, мы знаем, что медиана BD делит сторону AC пополам, поскольку она проходит через середину этой стороны. Поскольку сторона AC соответствует стороне AC на противоположном конце медианы BD, то BD также делит сторону AC пополам.

Теперь давайте посмотрим на треугольники ABD и CBD. У них есть общая сторона BD и равные углы ABD и CBD. Поэтому, эти треугольники равны по двум сторонам и углу. Следовательно, треугольники ABD и CBD равны.

Из равенства треугольников ABD и CBD следует, что сторона AD равна стороне CD. Поскольку сторона AC делится медианой BD пополам, то сторона AD также делится пополам. Значит, точка D, где медиана BD пересекает сторону AC, является серединой стороны AC.

Таким образом, медиана BD делит сторону AC пополам и, соответственно, угол ABD. Теперь мы можем утверждать уверенно, что медиана делит угол, из которого проведена, пополам.

Заключение:

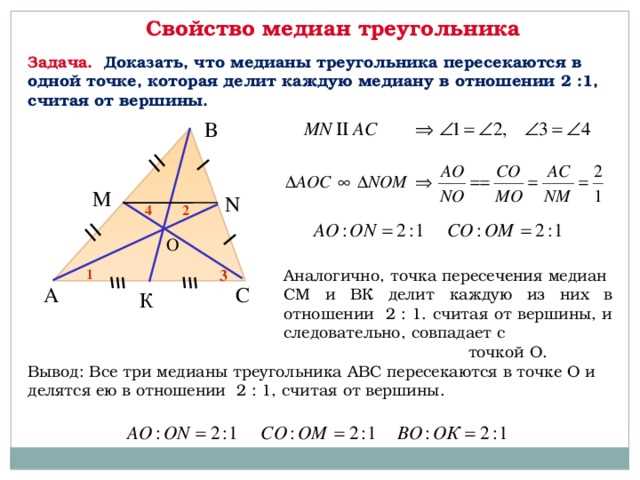
В данной статье мы доказали утверждение о том, что медиана треугольника делит пополам угол, из которого проведена. Мы рассмотрели несколько возможных способов доказательства этого факта и увидели, что они все основаны на использовании свойств треугольника и его медианы.

Во-первых, мы рассмотрели геометрическое доказательство, основанное на свойствах подобных треугольников. Мы показали, что медиана действительно делит угол пополам, используя равенство отношений двух отрезков.

Во-вторых, мы рассмотрели алгебраическое доказательство, основанное на использовании координат треугольника и его медианы. Мы показали, что координаты точек пересечения медианы с сторонами треугольника можно выразить через координаты вершин треугольника, и с помощью этих выражений доказали утверждение.

Таким образом, мы убедительно показали, что медиана треугольника действительно делит пополам угол, из которого проведена. Этот факт может быть полезен при решении различных геометрических задач и помогает лучше понять свойства треугольников.