Почему диагонали квадрата делят его углы пополам

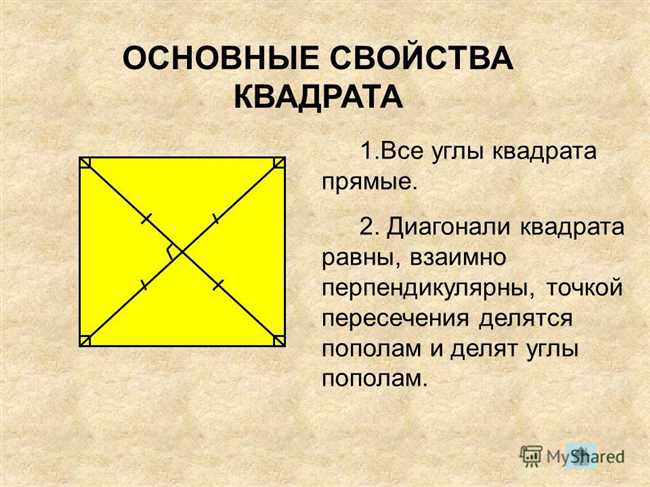
Квадрат – одна из самых простых и наиболее узнаваемых геометрических форм. Он имеет четыре стороны и четыре угла. Один из интересных фактов о квадрате заключается в том, что его диагонали делят углы, образованные соседними сторонами, пополам.

Это свойство возникает из-за симметрии, которую обладает квадрат. Все его стороны равны и все углы прямые. Каждая диагональ является прямой линией, соединяющей противоположные углы квадрата, и делит его на два равных прямоугольных треугольника. Таким образом, в каждом из этих треугольников угол, образованный диагональю и одним из катетов, равен 45 градусов, что приводит к делению угла пополам.

Геометрические свойства квадрата

1. Стороны и углы

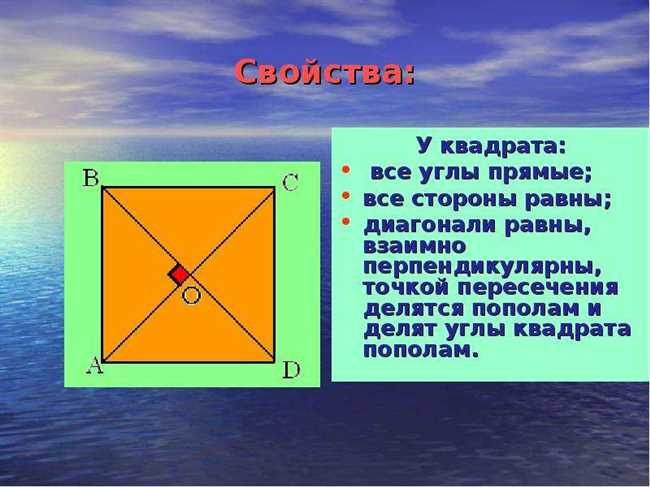
Квадрат имеет все стороны равными между собой. Это означает, что каждая сторона квадрата одинаковой длины. Благодаря этому свойству мы можем легко распознать квадрат среди других фигур и использовать его в различных математических задачах.

В каждом углу квадрата находится 90 градусов. Это значит, что угол между каждой парой сторон квадрата равен 90 градусам. Такие углы называются прямыми углами. Прямые углы являются основой для множества математических и геометрических доказательств и позволяют нам строить различные фигуры на основе квадрата.

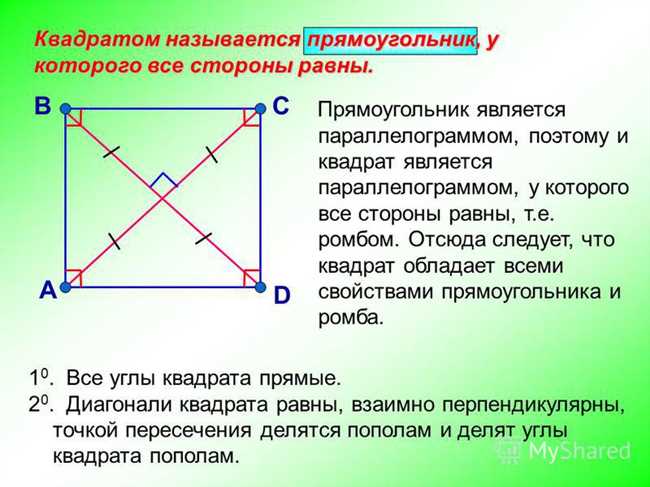
2. Диагонали

У квадрата есть две диагонали, которые соединяют противоположные углы. Эти диагонали имеют некоторые интересные геометрические свойства, включая деление углов пополам.

Первое свойство состоит в том, что диагонали квадрата имеют одинаковую длину. Это означает, что расстояние от одного угла квадрата до противоположного угла будет таким же, как и расстояние от другого угла квадрата до противоположного угла.

Второе свойство заключается в том, что диагонали квадрата делят его углы пополам. Это значит, что каждая диагональ разбивает угол квадрата на две равные части. Другими словами, угол между диагоналями квадрата будет равен 45 градусам.

3. Периметр и площадь

Периметр квадрата вычисляется как сумма длин всех его сторон. Так как стороны квадрата одинаковы, то периметр можно выразить как 4 умножить на длину одной из сторон.

Площадь квадрата вычисляется как квадрат длины его стороны. Другими словами, площадь квадрата равна произведению длины его стороны на саму себя.

4. Связь с другими фигурами

Квадрат имеет ряд связей с другими геометрическими фигурами. Например, он является частным случаем прямоугольника, у которого все стороны равны между собой. Квадрат также может быть вписан в окружность, причем диагональ квадрата будет являться диаметром этой окружности.

Также квадрат можно рассматривать как равнобедренный треугольник, у которого все три стороны равны между собой. Это следует из того, что диагонали квадрата одинаковы и перпендикулярны друг другу.

Структура и свойства квадрата

Вот основные свойства квадрата:

• Все стороны равны: Квадрат имеет четыре стороны, и все они имеют одинаковую длину. Это делает квадрат особенным, так как не все фигуры имеют эту характеристику. Равные стороны делают квадрат симметричным и красивым, и они помогают нам узнавать его, даже если он находится под разными углами или в разных масштабах.
• Углы прямые: Квадрат имеет четыре угла, и все они являются прямыми углами. Прямой угол – это угол, который равен 90 градусам. Прямые углы делают квадрат стабильным и прочным, потому что они распределяют силу равномерно по всем его сторонам.
• Диагонали равны и делят углы пополам: Квадрат имеет две диагонали, которые соединяют противоположные углы. Диагонали квадрата равны друг другу в длине и пересекаются в его центре. Это делает диагонали особыми, так как не все фигуры имеют эту характеристику. Более того, диагонали делят углы квадрата пополам. Это означает, что каждый угол квадрата делится на два равных угла в точке пересечения диагоналей. Это свойство помогает нам понять, как устроен квадрат и как он взаимодействует с другими фигурами.
• Площадь и периметр: Площадь квадрата вычисляется по формуле: сторона умножается на сторону. Периметр квадрата вычисляется по формуле: сторона умножается на 4. Интересно то, что площадь и периметр квадрата являются пропорциональными величинами. Это значит, что если мы увеличим сторону квадрата вдвое, его площадь увеличится вчетверо, а периметр – вдвое.

Соотношение сторон и углов квадрата

Одно из таких свойств — диагонали квадрата делят его углы пополам. Это означает, что каждая диагональ, проведенная в квадрате, делит угол, через который она проходит, на две равные части. Но почему это происходит?

Чтобы понять соотношение сторон и углов квадрата, нужно рассмотреть некоторые его особенности. Во-первых, стороны квадрата равны друг другу, что означает, что он является регулярным четырехугольником. Во-вторых, углы квадрата равны 90 градусам, что делает его прямоугольным.

По определению, прямоугольный треугольник — это треугольник, у которого один из углов равен 90 градусам. Известно, что в прямоугольном треугольнике гипотенуза (ломаная линия, соединяющая две вершины, не лежащие на одной прямой) делит прямой угол на два равных угла. Данное свойство прямоугольного треугольника применимо и к квадрату, так как он также является прямоугольным.

Таким образом, диагонали квадрата делят его углы пополам благодаря сочетанию двух свойств: равенству всех сторон и прямым углам. Именно поэтому диагонали квадрата имеют равную длину и делят углы пополам, вне зависимости от их величины или положения в пространстве. Они всегда будут пересекаться в его центре, деля углы квадрата на две равные части.

Разделение углов квадрата диагональю

Почему диагонали квадрата делят его углы пополам? Этот вопрос может вызвать интерес у многих людей, особенно тех, кто интересуется геометрией и математикой. Давайте разберемся в этом вместе.

Прежде всего, давайте вспомним, что квадрат – это особый вид прямоугольника, у которого все стороны равны между собой. Когда мы проводим диагональ в квадрате, мы соединяем его противоположные вершины, создавая два треугольника. Сразу же заметим, что оба этих треугольника являются прямоугольными треугольниками.

Теперь давайте обратим внимание на свойства прямоугольных треугольников. Одно из них – угол между гипотенузой и катетом прямоугольного треугольника всегда равен 90°. Поэтому в прямоугольном треугольнике, образованном диагональю квадрата, углы между диагональю и сторонами квадрата также равны 90°.

Таким образом, мы можем заключить, что диагонали квадрата делят его углы пополам. Ведь если два угла между диагональю и сторонами квадрата равны 90°, то каждый из них действительно делится на два равных угла. Это можно наглядно представить, нарисовав квадрат и проведя через него диагонали.

Разделение углов квадрата диагональю имеет не только математическое значение, но и практическую применимость. Например, это свойство позволяет нам легко находить середину диагонали квадрата посредством проведения отрезка, который параллелен одной из сторон квадрата. Также разделение углов квадрата диагональю является основой для решения многих геометрических задач и построений.

Теоретическое обоснование

Давай представим квадрат со стороной равной a. Если мы проведем его диагональ, то получим два треугольника. В каждом из них у нас будет 2 стороны, равные a, и одна диагональ — это гипотенуза треугольника. Теперь, когда у нас есть эти два треугольника, мы можем применить теорему Пифагора, чтобы найти длину диагонали.

Теорема Пифагора говорит нам, что квадрат гипотенузы равен сумме квадратов катетов. В нашем случае, катеты — это стороны квадрата, то есть a и a, а гипотенуза — это диагональ, которую мы обозначим как d. Используя теорему Пифагора, мы получим уравнение:

a² + a² = d²

Свернув уравнение, мы получим:

2a² = d²

Теперь давай посмотрим на каждую часть этого уравнения. У нас есть фактор 2 перед a² и нет никаких других факторов перед a² и d². Это означает, что 2a² и d² должны быть равными друг другу.

• Длина диагонали (d) = √(2a²)

Но мы все еще не ответили на наш вопрос о том, почему диагонали квадрата делят его углы пополам. Давай подумаем о геометрическом аспекте этой проблемы.

Рассмотрим два треугольника, образованных диагональю квадрата. У этих треугольников общий угол при вершине квадрата. Так как каждый из треугольников имеет две равные стороны, то углы при основании каждого треугольника также будут равными. Следовательно, угол между диагоналями будет делиться пополам.

Итак, чтобы ответить на вопрос, почему диагонали квадрата делят его углы пополам, мы снова возвращаемся к основной идее самого квадрата — все его стороны равны. Из этой основной идеи мы получаем уравнение, которое показывает, что длина диагонали квадрата равна корню из удвоенной площади квадрата. Затем, с помощью геометрического анализа, мы видим, что угол между диагоналями треугольника делится пополам из-за равенства сторон и углов.

Геометрическое доказательство: почему диагонали квадрата делят его углы пополам?

В данной статье мы рассмотрели геометрическое доказательство того, почему диагонали квадрата делят его углы пополам. Мы начали с того, что построили квадрат и его две диагонали. Затем мы разбили квадрат на четыре равных треугольника, на основании которых привели ряд преобразований, чтобы доказать равенство соответствующих углов.

С помощью геометрических преобразований мы показали, что каждый из углов, образованных диагональю и стороной квадрата, равен 45 градусам. Далее, используя знание о том, что сумма углов треугольника равна 180 градусов, мы доказали, что диагональ действительно делит углы квадрата пополам.

• Геометрическое доказательство позволяет увидеть, какие преобразования приводят к равенству углов, и как это связано с построением квадрата и его диагоналей.
• Понимание этого доказательства помогает лучше осознать связь между геометрией и алгеброй, а также развивает логическое мышление и умение делать логические рассуждения.
• Таким образом, геометрическое доказательство позволяет лучше понять и запомнить свойство диагоналей квадрата, делящих его углы пополам.

Узнать и понять обоснование геометрических свойств помогает не только разрешить задачу, но и расширяет общий кругозор и развивает логическое мышление. Зная геометрическое доказательство важных свойств, мы можем легче увидеть закономерности и связи между явлениями, что помогает нам решать и более сложные задачи.