Почему 0 в степени 0 равно 1: математическая тайна разгадана

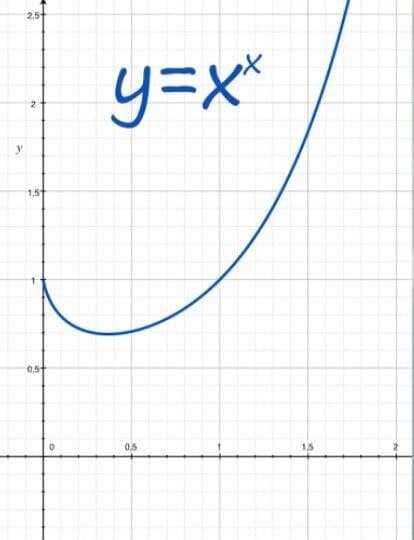
Есть одна интересная и загадочная математическая тайна, которая вызывает у людей много вопросов: почему 0 в степени 0 равно 1? Несмотря на то, что может показаться нелогичным, это утверждение действительно верно и доказано математиками. Однако, объяснить это явление не так просто.

Если мы обратимся к определению степеней, то увидим, что число в степени 0 всегда равно 1. Но что происходит, когда сама степень является нулевой? Здесь на помощь приходит теория пределов и специальные математические методы, которые позволяют нам получить ответ 1 для 0 в степени 0.

Почему именно так получается и как это связано с основными математическими законами — об этом и многом другом в нашем объяснении математической тайны. Погрузитесь в этот увлекательный мир чисел и найдите ответы на свои вопросы!

Что такое степень?

Например, если мы возьмем число 2 и возведем его в степень 3, то это будет означать, что мы умножаем 2 на само себя три раза: 2 * 2 * 2 = 8. В данном случае число 2 является основанием, а число 3 — показателем степени.

Однако степень может быть и отрицательным числом. В этом случае основание записывается в знаменателе и возводится в отрицательную степень.

Например, возьмем число 5 и возведем его в степень -2. В данном случае получится 1/5^2 = 1/25. Здесь 5 является основанием, -2 — показателем степени, а результатом будет обратное число основания, возведенное в положительную степень.

Степень также может быть и дробным числом. В этом случае основание изначально должно быть положительным числом.

Например, возьмем основание 4 и возведем его в степень 1/2. Получим корень квадратный из 4, что равно 2.

Таким образом, степень — это способ записи умножения числа на само себя, применяемый для работы с различными операциями в математике.

Определение понятия степень в математике

Понятие степени часто используется для удобного выражения больших чисел. Так, если число a возводится в степень n, то результатом будет a, умноженное само на себя n раз.

Степень обозначается в виде a^n, где a называется основанием, а n — показателем степени.

Основной случай — это возведение числа в положительную степень. Например, число 2 возводится в степень 3, и мы получаем 2^3 = 2 * 2 * 2 = 8.

Однако степень может быть и отрицательной. Если a возводится в отрицательную степень, то результат равен обратному числу, возведенному в положительную степень: a^(-n) = 1 / a^n.

Также степень может быть равна нулю. В этом случае результат всегда равен 1. Это может показаться странным и вызвать вопросы, но существуют математические причины для такого определения.

Это связано с тем, что степень с нулевым показателем имеет особое значение в математических операциях и позволяет соблюдать определенные правила и законы.

Вот несколько примеров:

• Число 2 возводим в степень 0: 2^0 = 1
• Число 3 возводим в степень 0: 3^0 = 1
• Число 5 возводим в степень 0: 5^0 = 1

Все эти примеры демонстрируют, что любое число, возводимое в степень 0, всегда равно 1.

Причина в том, что когда мы умножаем число на 1, оно сохраняет свою исходную величину, поэтому 1 является нейтральным элементом при умножении.

Таким образом, определение того, что 0 в степени 0 равно 1, удовлетворяет математическим правилам и принимается в математическом сообществе.

Правила операций со степенями

1. Умножение степеней с одинаковым основанием

Если у нас есть две степени с одинаковым основанием, то их можно перемножить, сложив показатели степени. Например:

• 2³ * 2⁴ = 2^{(3 + 4)} = 2⁷ = 128
• x² * x⁵ = x^{(2 + 5)} = x⁷

2. Деление степеней с одинаковым основанием

Если у нас есть две степени с одинаковым основанием, то их можно разделить, вычтя показатели степени. Например:

• 7⁵ / 7² = 7^{(5 — 2)} = 7³ = 343
• a⁴ / a¹ = a^{(4 — 1)} = a³

3. Возведение в степень степени

Если у нас есть число, возведенное в степень, и это число снова возводится в степень, то показатели степени умножаются. Например:

• (2³)² = 2^{(3 * 2)} = 2⁶ = 64
• (a⁴)³ = a^{(4 * 3)} = a¹²

4. Умножение степени на обычное число

Степень можно умножить на обычное число путем увеличения показателя степени на это число. Например:

• 2⁴ * 3 = 2⁴ * 2¹ = 2^{(4 + 1)} = 2⁵ = 32
• x³ * 5 = x³ * x⁰ * 5 = x^{(3 + 0)} * 5 = x³ * 5

5. Деление степени на обычное число

Степень можно разделить на обычное число путем уменьшения показателя степени на это число. Например:

• 5³ / 2 = 5³ / 5¹ / 2 = 5^{(3 — 1)} / 2 = 5² / 2 = 25 / 2
• b⁴ / 4 = b⁴ / b² / 4 = b^{(4 — 2)} / 4 = b² / 4

Зная правила операций со степенями, мы можем легко выполнять различные вычисления и решать математические задачи. Уверены, что вы овладеете этими правилами и сможете использовать их для успешного решения задач и проблем, связанных со степенями!

Основные правила операций со степенями

Возведение в степень

Возведение в степень — это операция, при которой число умножается само на себя заданное количество раз. Правило возведения в степень выглядит следующим образом:

Если число a возводится в положительную целую степень n, то результатом будет a, умноженное на себя n раз: aⁿ = a * a * … * a

Например, 2³ = 2 * 2 * 2 = 8.

Если степень n равна 0, то результатом будет 1: a⁰ = 1. Например, 2⁰ = 1.

Если числа a и b являются положительными, а их степени n и m также положительны, то выполняются следующие правила умножения и деления степеней:

Умножение степеней с одинаковыми основаниями

Если у нас есть степени с одинаковым основанием, мы можем перемножить их и сложить показатели степеней:

aⁿ * a^m = a^n+m

Например, 2³ * 2⁴ = 2⁷ = 128.

Деление степеней с одинаковыми основаниями

Если у нас есть степени с одинаковым основанием, мы можем разделить их и вычесть показатели степеней:

aⁿ / a^m = a^n-m

Например, 4⁵ / 4³ = 4² = 16.

Возведение в степень степени

При возведении числа в степень, которая сама является степенью, мы можем перемножить показатели степеней:

(aⁿ)^m = a^n*m

Например, (2³)² = 2^3*2 = 2⁶ = 64.

Умножение и деление степеней с разными основаниями

Если у нас есть степени с разными основаниями, мы не можем просто перемножить или разделить их. В этом случае каждое основание должно быть возведено в соответствующую степень:

(a * b)ⁿ = aⁿ * bⁿ

(a / b)ⁿ = aⁿ / bⁿ

Например, (2 * 3)² = 2² * 3² = 4 * 9 = 36.

Возведение в отрицательную степень

Если число возводится в отрицательную степень, то обратная величина числа должна быть возведена в положительную степень:

a^-n = 1 / aⁿ

Например, 2^-3 = 1 / 2³ = 1 / 8 = 0.125.

Возведение в дробную степень

Если число возводится в дробную степень, мы можем использовать правило корня:

a^m/n = √ⁿ(a^m)

Например, 8^2/3 = √³(8²) = √³(64) = 4.

Ознакомившись с этими основными правилами операций со степенями, вы сможете выполнять математические операции более уверенно и эффективно. И помните, практика делает мастера!

Исключение: 0 в степени 0

Однако, существует небольшое исключение, при котором 0 в степени 0 равно 1. Это правило основано на математическом рассуждении и может быть убедительным только в определенном контексте.

Рассмотрим следующий пример: у нас есть функция f(x) = x^0. Если мы подставим в эту функцию любое число, кроме 0, получим результат равный 1. Например, f(2) = 2^0 = 1, f(3) = 3^0 = 1 и так далее. Это значит, что при возводении числа в степень 0, результат всегда будет равен 1.

Теперь давайте рассмотрим другой пример: f(0) = 0^0. Если мы хотим, чтобы наше правило f(x) = x^0 сохранилось и в этом случае, то мы должны признать, что 0^0 = 1. Это согласуется с другими правилами алгебры, такими как 0^n=0, где n — любое положительное число.

Хотя это правило вызывает некоторые парадоксы и отступления от общепринятых математических правил, оно может быть полезным и использоваться в некоторых областях математики и физики. Например, в комбинаторике, теории вероятностей и теории чисел. Также оно позволяет упростить некоторые вычисления и удобно использовать в некоторых формулах и уравнениях.

В заключении, хоть вопрос о том, что такое 0 в степени 0, остается открытым и подлежит дальнейшим исследованиям, существует небольшое исключение, при котором можно считать, что 0 в степени 0 равно 1. Это исключение находит свое применение в определенных областях математики и физики, и может помочь в упрощении некоторых расчетов и формул.

Почему 0 в степени 0 равно 1: объясняем математическую тайну

Рассматриваем специальный случай 0 в степени 0

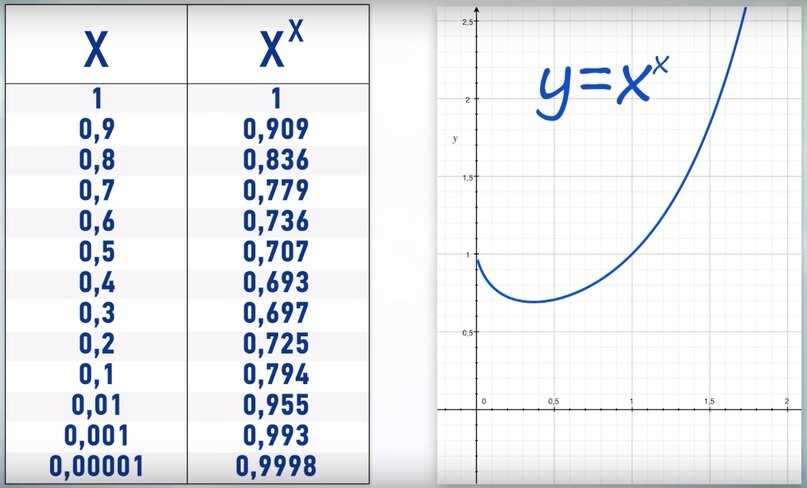
На первый взгляд, казалось бы, что 0 возведенное в любую положительную или отрицательную степень равно 0. Однако, когда мы рассматриваем специальный случай 0 в степени 0, возникает различие в мнениях математиков.

Одна из интерпретаций гласит, что 0 в степени 0 равно 1. Это объясняется тем, что степень — это повторение умножения числа на само себя определенное количество раз. В случае с 0 в степени 0, мы не умножаем ни на что, но обычно соглашение говорит, что любое число в степени 0 равно 1. Таким образом, 0 в степени 0 тоже может быть равно 1.

Однако, другая интерпретация утверждает, что 0 в степени 0 не имеет определенного значения. Это объясняется тем, что мы не можем однозначно определить, какое число должно быть результатом операции. Например, если мы рассмотрим последовательность чисел, где каждое следующее число делится на предыдущее, то при достижении 0 ситуация становится сложной. Мы не можем однозначно определить, какое число должно быть результатом деления 0 на 0, и поэтому можем сказать, что 0 в степени 0 не имеет определенного значения.

В итоге, вопрос о значении 0 в степени 0 остается открытым и до сих пор вызывает полемику среди математиков. Возможно, в будущем, появятся новые теории и доказательства, которые помогут пролить свет на эту загадку. Однако, пока что, мы можем лишь рассматривать различные интерпретации и дискутировать на эту тему.

Различные подходы к решению

Один из подходов, который можно назвать «привычным», гласит, что ноль в степени нуля не имеет определенного значения и является неопределенностью. Этот подход основан на том, что при возведении числа в степень, мы умножаем его само на себя определенное количество раз. Нуль не имеет смысла умножать на себя, поэтому его степень не имеет смысла и равна неопределенности.

Другой подход, который можно назвать «формальным», основан на определении степени через произведение. Согласно этому подходу, ноль в степени нуля равен 1 по определению. Если мы оставим в определении произведения только один множитель, то получим, что ноль в степени нуля равен 1.

Третий подход, называемый «граничным», основан на анализе пределов функций. Этот подход позволяет вычислить значение нуля в степени нуля, используя пределы функций, которые сходятся к этому значению. В результате анализа пределов, получается, что ноль в степени нуля равен 1.

• Привычный подход: ноль в степени нуля — неопределенность
• Формальный подход: ноль в степени нуля равен 1
• Граничный подход: ноль в степени нуля равен 1

В каждом из подходов есть свои аргументы и обоснования, и каждый из них может быть валидным. Вопрос о значении нуля в степени нуля остается открытым и спорным, и именно это делает его таким интересным для исследования и обсуждения.

В конечном счете, выбор подхода к решению этого вопроса остается на усмотрение математика или исследователя. Какой бы подход к решению вы ни приняли, важно помнить, что математика — это наука, которая строится на логических доказательствах и аргументах. Поэтому при обсуждении таких сложных вопросов, как значение нуля в степени нуля, необходимо приводить аргументы и доказательства, чтобы подкрепить свою точку зрения.

Описываем различные точки зрения на вопрос 0 в степени 0

Вопрос о том, что равностепенность числа 0 в степени 0, вызывает жаркие споры и даже контроверзии среди математиков и ученых уже на протяжении многих лет. Существует несколько различных точек зрения относительно этого вопроса, что создает дополнительные сложности при его решении.

Точка зрения №1: Ноль в степени ноль является неопределенным значением и не имеет определенного результата. Сторонники этой точки зрения утверждают, что нельзя точно определить, что равностепенность 0 в степени 0, поскольку нет строгой математической основы для этого. Они считают, что пытаться найти значение для этого выражения бессмысленно.

Точка зрения №3: Значение 0 в степени 0 является асимптотическим и зависит от контекста. Сторонники этой точки зрения утверждают, что значение 0 в степени 0 может быть определено только в рамках конкретной математической задачи или уравнения. В некоторых ситуациях значение может быть равно 1, в других — 0, а в некоторых — бесконечности. Подход к определению значения 0 в степени 0 должен учитывать особенности конкретной задачи, в которой оно используется.

Таким образом, ответ на вопрос о значении 0 в степени 0 не является однозначным и зависит от того, какой точки зрения придерживается каждый человек. Он может быть равен 1, неопределен или зависеть от контекста. Каждая точка зрения имеет свои аргументы и мнения последователей. Важно помнить, что математика — это наука, которая постоянно развивается, и что некоторые вопросы все еще остаются открытыми для дальнейшего исследования и обсуждения.

Математические доказательства

Преимущества математических доказательств:

• Они обеспечивают точность и надежность математических утверждений.
• Позволяют избежать ошибок и иррациональных умозаключений.
• Устанавливают справедливость математических утверждений независимо от субъективных представлений и мнений.
• Создают единое математическое ядро, на котором базируется вся наука.
• Позволяют развивать новые математические теории и открывать новые области знаний.

Математические доказательства являются незаменимым инструментом для установления и проверки математических фактов. Они позволяют математикам достичь точности, строгости и надежности в своих исследованиях. Благодаря математическим доказательствам математика продолжает развиваться и находить применение во всех областях науки и жизни.