
Когда речь идет о прямоугольниках, одной из их характеристик является наличие перпендикулярных диагоналей. Перпендикулярные диагонали встречаются только в прямоугольниках и квадратах, что делает это свойство уникальным для данных фигур.
Перпендикулярные диагонали имеют следующие особенности: они равны по длине и пересекаются в точке, которая делит их пополам. Кроме того, каждая диагональ является осью симметрии для прямоугольника. Это означает, что фигура может быть разделена на две одинаковые части относительно диагоналей.
Свойство перпендикулярных диагоналей определяет основные характеристики прямоугольника и позволяет различать его от других геометрических фигур. Практическое применение этого свойства включает использование прямоугольников в архитектуре, строительстве, дизайне и других областях, где важна точность и симметричность.
Свойство прямоугольника
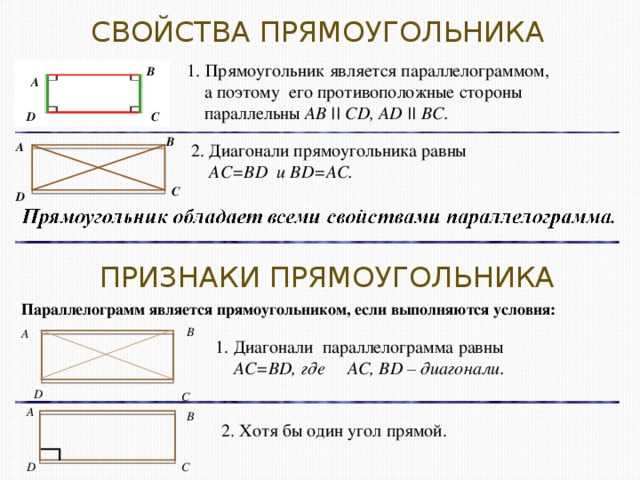
Перпендикулярные диагонали – это такие диагонали, которые пересекаются под прямым углом. Именно это свойство делает прямоугольник особенным и уникальным.
Давайте рассмотрим эту особенность прямоугольника подробнее. Если мы нарисуем диагонали внутри прямоугольника, они будут пересекаться точно в его центре. А угол между этими диагоналями всегда будет равен 90 градусам. Ведь пересекающиеся прямые всегда образуют прямой угол!
Зачем нам знать об этом свойстве прямоугольника? Это может быть полезно во многих ситуациях. Например, если мы знаем, что диагонали прямоугольника перпендикулярны, то можем легко найти их длины, а также решать различные задачи, связанные с прямоугольником.
Также нам может потребоваться знать, что диагонали прямоугольника равны между собой. Действительно, если мы проведем две диагонали внутри прямоугольника, то они будут иметь одинаковую длину.
Вы уже представляете, какая прекрасная фигура – прямоугольник? Его перпендикулярные диагонали делают его особенным и удобным для решения различных задач и проблем.
Так что давайте обратим внимание на эту интересную особенность прямоугольника и использовать ее в нашей повседневной жизни! Уверен, вы уже не посмотрите на эту простую фигуру так же, как раньше.
Перпендикулярные диагонали

Прямоугольники, как вы, безусловно, знаете, имеют четыре угла, из которых два противолежащих являются прямыми (90 градусов). А что, если я скажу, что диагонали прямоугольника также пересекаются под прямым углом?
Вопрос: Как же это происходит?
Ответ: Пусть у нас есть прямоугольник ABCD с диагоналями AC и BD. Если вы нарисуете эти две диагонали, они пересекутся в точке O, которая является центром прямоугольника. Мы можем доказать, что эти диагонали перпендикулярны, используя геометрические свойства прямоугольника.
Почему это важно, вы спросите? Потому что это свойство перпендикулярных диагоналей является основой для ряда других свойств и теорем о прямоугольниках.
А теперь давайте рассмотрим некоторые интересные аспекты перпендикулярных диагоналей:
- Перпендикулярные диагонали являются основой для расчета площади и периметра прямоугольника.
- Они помогают определить углы и стороны прямоугольника, а также его диагонали.
- Математические связи между перпендикулярными диагоналями используются в множестве задач и проблем в различных областях, таких как геометрия, физика и инженерное дело.
- Это свойство также имеет практическое применение в строительстве, дизайне и архитектуре, где прямоугольники часто используются для создания структур и объектов.
Таким образом, перпендикулярные диагонали — это удивительное свойство прямоугольников, которое открывает перед нами множество возможностей и применений. Они позволяют нам лучше понять и использовать прямоугольники в нашей повседневной жизни и профессиональной деятельности. Разумеется, математика играет ключевую роль в понимании и применении этого свойства, но в конечном итоге оно становится гораздо более доступным и полезным для нас.
Геометрическое доказательство перпендикулярности диагоналей прямоугольника
Рассмотрим простое геометрическое доказательство этого свойства.
Шаг 1: Нарисуем произвольный прямоугольник ABCD на плоскости.

Шаг 2: Нарисуем диагонали AC и BD, соединяющие противоположные вершины прямоугольника.

Шаг 3: Построим отрезок EF, перпендикулярный диагонали BD и проходящий через середину её, то есть точку M.

Шаг 4: Рассмотрим треугольники BNA и CMA.

Учитывая, что прямоугольник имеет прямые углы, угол BNA является прямым, а значит, треугольник BNA — прямоугольный.
Также, по построению отрезка EF, угол EFM является прямым, а значит, треугольник CMA — прямоугольный.
- Таким образом, мы имеем следующее:
- Треугольник BNA — прямоугольный (из шага 4)
- Треугольник CMA — прямоугольный (из шага 4)
- Угол BNA и угол CMA — общие прямые углы (принадлежат всем двум треугольникам)
Таким образом, диагонали BD и AC пересекаются и образуют взаимно перпендикулярные линии, что является свойством прямоугольника.
Такое геометрическое доказательство перпендикулярности диагоналей прямоугольника базируется на принципе равенства прямых углов и приводит к более полному пониманию этой математической концепции.
С прямоугольниками мы сталкиваемся практически на каждом шагу. Они присутствуют в архитектуре, строительстве, дизайне и других отраслях нашей повседневной жизни. Поэтому знание основных свойств прямоугольников, таких как перпендикулярные диагонали, является важным и полезным.
Практическое применение
Одним из практических примеров использования данного свойства является строительство. Зная, что диагонали прямоугольника перпендикулярны друг другу, строители могут использовать эту информацию для выравнивания стен и углов здания. Это позволяет им создавать прямые и устойчивые конструкции, которые соответствуют строительным стандартам и требованиям безопасности.
Еще одним примером практического применения этого свойства является геометрия. Математики и инженеры используют перпендикулярные диагонали для измерения и расчетов. Например, при построении картографических систем или создании компьютерных моделей, перпендикулярные диагонали помогают расставить точки и измерить расстояния и углы. Это позволяет создавать более точные и точные модели в разнообразных областях, таких как геодезия и архитектура.
Важно отметить, что практическое применение свойства прямоугольника с перпендикулярными диагоналями не ограничивается только строительством и геометрией. Это свойство также может быть использовано в других областях, таких как дизайн, искусство, фотография, разработка игр и т. д. Перпендикулярные диагонали могут быть использованы для создания симметричных и гармоничных композиций, ориентирования объектов или создания эффектов перспективы.






