Перпендикуляр ли две прямые к третьей прямой или это лишь заблуждение?

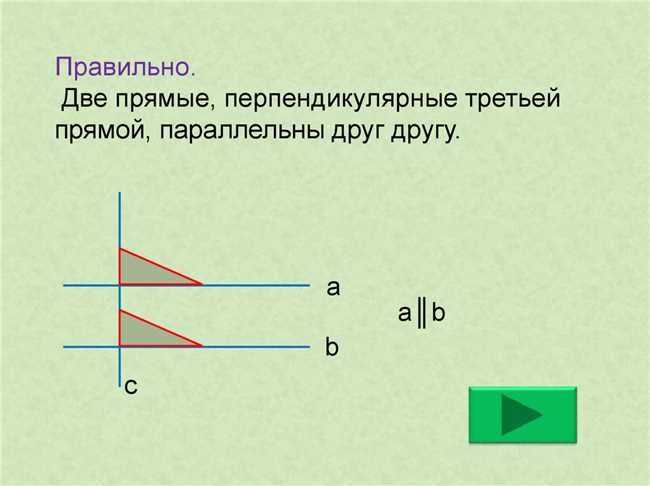
Думают многие, что две прямые могут быть перпендикулярными к третьей. Но на самом деле это утверждение не совсем верно. По определению, перпендикулярные прямые должны пересекаться и образовывать прямой угол. Если бы мы рассматривали перпендикулярность в контексте трех прямых, то все три прямые должны были бы пересекаться и образовывать как минимум два угла. Однако, в случае двух перпендикулярных прямых, третья прямая не сможет пересечь обе, так как они лежат в плоскости, параллельной третьей прямой. Таким образом, две прямые не могут быть перпендикулярными к третьей прямой.

Раздел 1: Определение перпендикулярности

Перпендикулярность — это особое отношение между двумя прямыми линиями, когда они пересекаются под прямым углом. Иными словами, две прямые считаются перпендикулярными, если они образуют прямой угол.

Это понятие является основополагающим в геометрии и широко используется в различных областях, включая архитектуру, инженерию и так далее. Понимание перпендикулярности помогает решать различные задачи, связанные с расположением и выравниванием объектов.

Теперь, когда мы знаем, что такое перпендикулярность, можно перейти к рассмотрению вопроса: могут ли две прямые быть перпендикулярными третьей прямой?

Ответ на этот вопрос достаточно простой и однозначный: да, две прямые могут быть перпендикулярными третьей прямой. Фактически, это одна из основных особенностей перпендикулярности.

Из определения перпендикулярности следует, что прямые A и B могут быть перпендикулярными друг к другу, а также обе могут быть перпендикулярны третьей прямой C. Все три прямые в этом случае образуют прямоугольный треугольник.

Примером такой ситуации является угол, образованный перекрестными прямыми на пересечении улиц. Две улицы могут пересекаться под прямым углом и быть перпендикулярными друг к другу, и каждая из них будет перпендикулярна третьей прямой, обозначающей третью улицу или дорогу.

Таким образом, ответ на вопрос «Могут ли две прямые быть перпендикулярными третьей прямой?» — да, они могут. Это является одной из основных особенностей перпендикулярности и широко используется в геометрии и других областях.

Раздел 2: Доказательство утверждения «Две прямые перпендикулярные третьей прямой»

Давайте разберемся, как доказать утверждение о двух прямых, которые перпендикулярны к одной и той же третьей прямой. Это очень интересное и важное утверждение в геометрии, которое часто используется при решении задач и построении фигур.

Первым шагом для доказательства этого утверждения является определение перпендикулярности. Две прямые считаются перпендикулярными, если они образуют прямой угол, то есть угол, равный 90 градусам.

• Аргумент 1: По определению прямого угла, он равен 90 градусам.

Теперь рассмотрим ситуацию, когда у нас есть третья прямая, которая пересекает одну из перпендикулярных прямых. Предположим, что эта прямая пересекает одну из перпендикулярных прямых в точке A.

Так как точка A лежит на перпендикулярной прямой, то угол между перпендикулярной прямой и третьей прямой составляет 90 градусов. Но угол между перпендикулярными прямыми тоже равен 90 градусам. Получается, что угол между третьей прямой и перпендикулярной прямой равен углу между перпендикулярными прямыми, то есть 90 градусам.

• Аргумент 2: Угол А между перпендикулярной прямой и третьей прямой равен 90 градусам, так как точка А лежит на перпендикулярной прямой.
• Аргумент 3: Угол B между перпендикулярными прямыми тоже равен 90 градусам, так как они перпендикулярны друг другу.

Итак, мы доказали утверждение о двух прямых, которые перпендикулярны к одной и той же третьей прямой. Такие прямые называются перпендикулярными плоскостями.

Надеюсь, мое объяснение было понятным и полезным для вас. Если у вас возникли вопросы или вы хотели бы узнать что-то еще о данной теме, не стесняйтесь задавать их. Я с радостью отвечу!

Раздел 3: Примеры перпендикулярных прямых

В предыдущих разделах мы уже узнали, что две прямые называются перпендикулярными, если они пересекаются под прямым углом. Теперь давайте рассмотрим несколько примеров таких перпендикулярных прямых.

Пример 1: Вертикальные и горизонтальные прямые

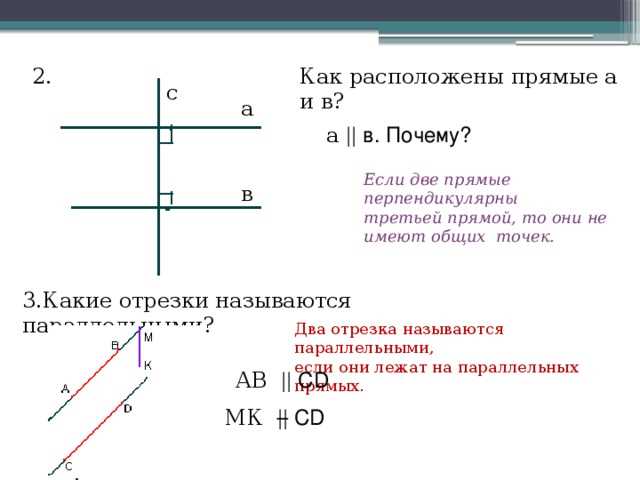
Первый пример – это вертикальные и горизонтальные прямые. Когда вертикальная прямая пересекает горизонтальную прямую, они образуют прямой угол, который равен 90 градусам. Это значит, что такие прямые перпендикулярны друг другу.

Например, представьте себе стены в комнате. Где бы вы ни поставили вертикальную прямую (например, шкаф), она перпендикулярна полу (который является горизонтальной прямой) в том месте, где они пересекаются.

Пример 2: Отрезки на графике

Второй пример связан с отрезками на графике. Если мы нарисуем отрезок, который идет вниз (в верх) и имеет некоторый угол наклона, и затем нарисуем отрезок, который идет влево (вправо) и имеет наклон под прямым углом к первому отрезку, то они будут перпендикулярными.

На практике это может выглядеть, например, как дорога, которая пересекает ограждение на перекрестке под прямым углом.

Пример 3: Углы налево и направо

Третий пример – это углы, которые поворачивают налево или направо. Рассмотрим ситуацию, где прямая улица пересекается со второй улицей, которая идет налево. Угол между ними будет прямым, поэтому они перпендикулярны друг другу.

Аналогично, если улица пересекается со второй улицей, которая идет направо, угол между ними также будет прямым, что означает, что они перпендикулярны друг другу.

Может быть, вы думали, что перпендикулярные прямые только встречаются в математике, но на самом деле они окружают нас повсюду в нашей повседневной жизни.

• Первый пример: вертикальные и горизонтальные прямые
• Второй пример: отрезки на графике
• Третий пример: углы налево и направо

Раздел 4: Критика утверждения «Две прямые перпендикулярные третьей прямой»

1. Координатный подход

Рассмотрим две прямые на плоскости, заданные уравнениями y = x и y = -x. Очевидно, что эти две прямые не пересекаются и не параллельны друг другу. Однако, они обе перпендикулярны третьей прямой y = 0. Из этого видно, что утверждение о том, что две прямые перпендикулярны третьей прямой, не всегда верно.

2. Пример с треугольником

Предположим мы имеем треугольник ABC, у которого сторона AB перпендикулярна третьей стороне AC. Но сторона BC параллельна стороне AC. В этом случае, прямые AB и BC перпендикулярны третьей стороне, но не перпендикулярны друг другу. Это еще один пример, показывающий, что необходимо быть осторожными с утверждением о перпендикулярности двух прямых третьей прямой.

3. Контрпримеры

Другой способ опровергнуть утверждение «две прямые перпендикулярны третьей прямой» — предоставить примеры, которые его опровергают. Мы уже рассмотрели два примера выше. Давайте рассмотрим еще один: если две прямые имеют одинаковый угол наклона, то они не могут быть перпендикулярны третьей прямой.