Отношение квадрата к параллелограмму — это интересная тема, которая вызывает много вопросов и дискуссий. Многие люди задаются вопросом: существует ли связь между этими двумя фигурами? Что делает квадрат особенным, а параллелограмм — нет? Ответ на этот вопрос может быть не таким простым, как кажется. Рассмотрение геометрических особенностей и свойств этих фигур поможет нам разобраться в этом вопросе. Давайте вместе исследуем эту тему и попытаемся раскрыть ее секреты.
Квадрат и параллелограмм: есть ли связь?
Возможно, вы когда-то задавались вопросом, существует ли связь между квадратом и параллелограммом. Сразу хочу вас заверить, что связь действительно есть, и она очень интересная!
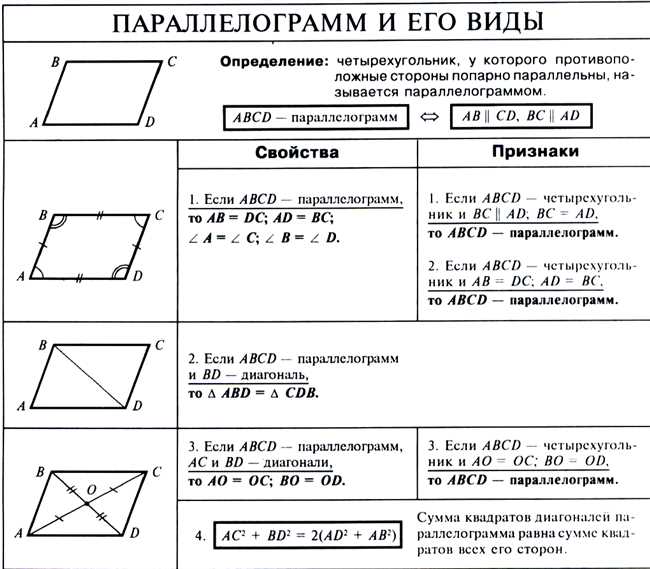
Давайте начнем с определений. Квадрат — это особый вид параллелограмма, представляющий собой фигуру с четырьмя прямыми равными сторонами и четырьмя прямыми равными углами. Таким образом, квадрат является параллелограммом по определению.
Между квадратом и параллелограммом существует несколько ключевых различий. Во-первых, у квадрата все стороны и углы равны, в то время как у параллелограмма могут быть разные размеры сторон и углы.
Во-вторых, квадрат можно представить как частный случай параллелограмма, в котором все стороны перпендикулярны друг другу. Это означает, что все углы квадрата равны 90 градусам. В то время как у параллелограмма углы могут быть разными, но противоположные углы всегда равны.
Квадрат имеет некоторые особенности, которые делают его важным и уникальным, и поэтому его связь с параллелограммом имеет большое значение. В частности, квадрат является регулярным многоугольником, что означает, что его стороны и углы равны. Это делает квадрат идеальной формой для многих приложений в геометрии, архитектуре, дизайне и других областях.
Например, вы когда-нибудь задумывались, почему многие города и деревни построены в виде квадрата или прямоугольника? Это связано с удобством и практичностью такого плана застройки. Квадрат и параллелограмм, в их разных проявлениях, используются в геометрическом планировании городских улиц, построении зданий и даже в обеспечении эффективного использования земельных участков.
Таким образом, связь между квадратом и параллелограммом заключается в том, что квадрат является особым видом параллелограмма, который обладает рядом уникальных свойств и применений. Они оба представляют собой важные концепции в геометрии и находят применение в различных областях жизни.
Геометрические определения
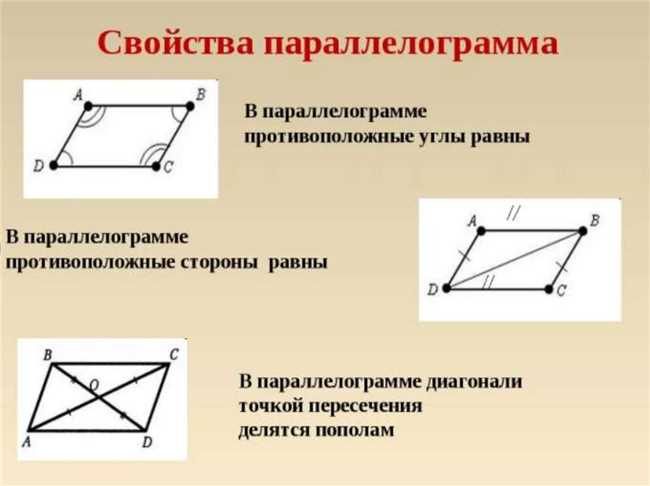
Параллелограмм — это фигура с двумя парами параллельных сторон. Параллельные стороны означают, что эти стороны никогда не пересекаются. Параллелограммы имеют такие свойства, как противоположные стороны, равные и параллельные диагонали, которые делят фигуру на две равные части. Это может быть сложно, но также очень интересно!
Итак, есть ли связь между квадратом и параллелограммом? Ответ — да, есть! Каждый квадрат является параллелограммом, но не каждый параллелограмм является квадратом. Квадрат — это частный случай параллелограмма, где все стороны одинаковые и все углы прямые. Это можно сказать и наоборот: каждый квадрат является частным случаем параллелограмма.
Также интересно знать, что квадрат — это ромб, у которого все углы прямые. Это означает, что каждый квадрат является ромбом, но не каждый ромб является квадратом.
Соотношение сторон и углов
Квадрат — это параллелограмм со свойством, что все его стороны равны между собой. Это означает, что у каждого угла квадрата равны между собой и составляют 90 градусов. Таким образом, соотношение сторон и углов в квадрате определено и неизменно.
С другой стороны, параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны между собой. Параллелограмм содержит два параллельных противоположных угла, которые также равны между собой. Однако, в отличие от квадрата, углы параллелограмма не обязательно равны 90 градусов.
Таким образом, соотношение сторон и углов в квадрате и параллелограмме имеет одну основную разницу — углы. В квадрате все углы равны 90 градусам, в то время как в параллелограмме углы могут быть разными.
Итак, ответ на вопрос о связи между квадратом и параллелограммом в отношении соотношения сторон и углов заключается в следующем: квадрат — это частный случай параллелограмма, для которого все углы равны 90 градусам и все стороны равны между собой.
Сходства и различия между квадратом и параллелограммом
Сходства:
- Четырехугольная форма: и квадрат, и параллелограмм состоят из четырех сторон и четырех углов.
- Геометрические свойства: обе фигуры имеют ряд общих геометрических свойств. Например, и квадрат, и параллелограмм имеют параллельные противоположные стороны и равные противоположные углы.
Различия:

- Углы: в квадрате все углы равны 90 градусам, в то время как в параллелограмме углы могут быть произвольными.
- Стороны: в квадрате все стороны равны между собой, тогда как в параллелограмме стороны могут быть разной длины.
- Диагонали: квадрат имеет две равные диагонали, пересекающиеся в центре фигуры под прямым углом, в то время как у параллелограмма диагонали не обязательно равны и могут иметь другой угол пересечения.
Также стоит отметить, что квадрат является особым типом параллелограмма, в котором все стороны и углы равны. Это значит, что каждый квадрат также является параллелограммом, но не каждый параллелограмм является квадратом.
Теперь, когда мы рассмотрели сходства и различия, вероятно, у вас возник вопрос: «Зачем это все знать?» Ответ прост: знание этих сходств и различий позволит вам более глубоко понять и анализировать геометрические фигуры. Может быть полезно, например, при решении задач или создании конструкций.
Заключение
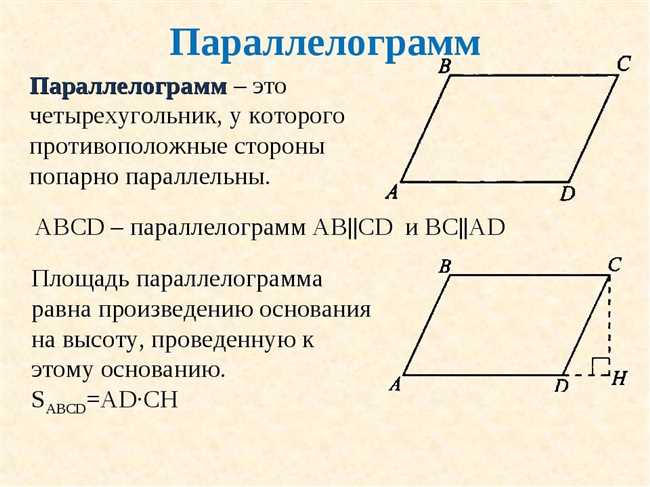
Однако, несмотря на то, что квадрат и параллелограмм имеют некоторые сходства, их практическое применение может отличаться. Рассмотрим некоторые практические примеры, где применение квадрата и параллелограмма может быть неодинаковым:
- Строительство и архитектура: В архитектуре часто используются прямоугольные формы, которые можно представить как квадраты или параллелограммы. Квадраты могут иметь символическое значение стабильности и симметрии, тогда как параллелограммы могут использоваться для создания интересных и необычных форм зданий.
- Дизайн и графика: Квадраты и параллелограммы играют важную роль в дизайне и графике. Знание и понимание отношений между этими фигурами помогает создавать гармоничные и сбалансированные композиции.
- Геометрические вычисления: В математике и физике отношение квадрата к параллелограмму имеет практическое значение при вычислении площади и периметра этих фигур. Квадрат имеет определенные свойства, которые делают его удобным для вычислений, например, все его стороны равны, а все углы прямые.






