Определение положения в пространстве: сопоставление точек и координат

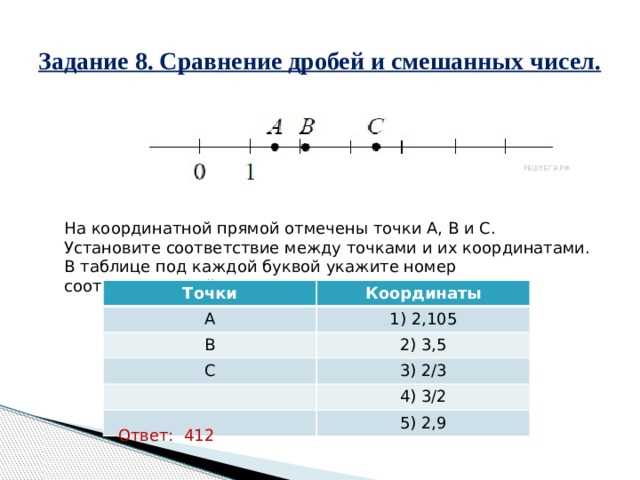
Гид по определению положения в пространстве: как установить соответствие между точками и их координатами

Когда речь заходит о навигации и перемещении в пространстве, определение положения является ключевым аспектом. Чтобы установить точное соответствие между точками и их координатами, необходимо использовать определенные методы и инструменты.

Понимание системы координат и принципов, лежащих в ее основе, является основой для определения точного положения. Одна из самых распространенных систем координат — декартова система, состоящая из осей X, Y и Z. Оси X и Y определены на плоскости, а ось Z — в трехмерном пространстве.

Чтобы определить точное положение, нужно знать значения координаты X, Y и Z. Координаты X и Y указывают на расстояние от начала координат до точки, а координата Z — высоту точки над плоскостью.

Существуют различные методы и технологии, позволяющие определить положение в пространстве с высокой точностью. Они включают в себя глобальные системы позиционирования (GPS), инерциальные системы навигации (INS), а также современные технологии виртуальной и дополненной реальности.

В этом гиде мы рассмотрим основы определения положения в пространстве и различные методы, которые могут помочь вам установить соответствие между точками и их координатами.

Определение положения в пространстве с помощью геометрических координат

Геометрические координаты — это система чисел, которая позволяет задать положение точки или объекта в пространстве. Основная идея заключается в том, чтобы сопоставить каждой точке уникальный набор чисел, который можно использовать для определения ее местоположения.

Система координат, наиболее часто используемая для определения положения в пространстве, называется декартовой системой координат. Она состоит из трех осей — X, Y и Z, которые пересекаются в точке, называемой началом координат.

Чтобы определить положение точки в декартовой системе координат, необходимо указать значения координаты X, Y и Z. Координата X отображает положение точки по горизонтальной оси, координата Y — по вертикальной оси, а координата Z — по оси, перпендикулярной плоскости X и Y.

Путем указания определенных значений координаты в каждом измерении мы можем точно определить положение точки в пространстве. Например, если мы имеем точку с координатами (2, 3, 1), это означает, что она расположена на оси X на расстоянии 2 единицы от начала координат, на оси Y — на расстоянии 3 единицы и на оси Z — на расстоянии 1 единицы.

Геометрические координаты не только помогают определить положение точки в пространстве, они также могут быть использованы для измерения расстояния между точками, определения углов и направлений, а также для решения различных геометрических задач.

Знание геометрических координат и умение работать с ними имеет широкий спектр применений в различных областях, таких как архитектура, инженерия, компьютерная графика и физика. Они позволяют нам более точно определить и манипулировать объектами в пространстве, предсказывать их поведение и создавать сложные модели и структуры.

В конечном счете, использование геометрических координат помогает нам лучше понять и взаимодействовать с окружающей нас физической средой. И они позволяют нам воплотить наши идеи и проекты в реальность.

Системы координат

Существует несколько различных систем координат, но две наиболее распространенные — декартова система координат и полярная система координат.

Декартова система координат

Декартова система координат, также известная как прямоугольная система координат, использует две перпендикулярные оси — горизонтальную (ось X) и вертикальную (ось Y). Каждой точке в пространстве соответствует уникальная пара значений (x, y), где x — значение на оси X, y — значение на оси Y.

Данная система координат широко используется для представления геометрических объектов, таких как точки, линии и фигуры. Зная значения x и y, мы можем точно определить положение объекта и его относительное расстояние от других объектов.

Полярная система координат

Полярная система координат использует радиус и угол для определения положения точки в пространстве. Точка задается значениями (r, θ), где r — расстояние от начала координат до точки (радиус), а θ — угол между положительным направлением оси X и линией, соединяющей начало координат и заданную точку.

Эта система координат наиболее удобна для описания круговых или радиальных движений, таких как вращение или расположение объекта относительно центральной точки.

Выбор системы координат

Выбор системы координат зависит от конкретной задачи, которую мы пытаемся решить. Декартова система координат обычно используется в евклидовом пространстве, где объекты могут иметь отрицательные и положительные значения на осях X и Y.

Полярная система координат наиболее полезна для работы с круговыми или радиальными движениями, где измерения ведутся относительно центральной точки.

Важно понимать, что системы координат — это всего лишь математические модели, которые помогают нам лучше понимать и решать задачи, связанные с положением и движением объектов в пространстве.

Определение точки по координатам

Для определения точки по координатам нужно знать систему координат, которую использует пространство, в котором находится точка. Наиболее распространенными системами координат являются прямоугольная и полярная системы координат.

Прямоугольная система координат

В прямоугольной системе координат плоскость делится на две оси: горизонтальную ось x и вертикальную ось y. Каждая ось имеет свою шкалу, на которой откладываются значения координат. Точка определяется своими координатами (x, y), где x — значение на горизонтальной оси, а y — значение на вертикальной оси.

Полярная система координат

В полярной системе координат точка определяется расстоянием от начала координат и углом, который образует радиус-вектор точки с положительным направлением оси x. Расстояние от начала координат до точки обозначается символом r, а угол обозначается символом θ.

Чтобы определить точку по координатам в полярной системе, нужно знать значение r и значение θ. Расстояние от начала координат до точки измеряется в положительных значениях, а угол измеряется в градусах или радианах.

Для чего нужно определение точки по координатам?

Определение точки по координатам имеет широкое применение в различных областях, таких как математика, физика, география, химия и технические науки.

• В математике координаты точек используются для нахождения расстояния между точками, нахождения углов и решения геометрических задач.
• В физике координаты точек используются для определения положения объектов в пространстве, скорости и ускорения объектов, а также для решения механических задач.
• В географии координаты точек используются для определения местоположения географических объектов, создания карт и навигации.
• В химии координаты точек используются для описания структуры молекул и решения химических задач.
• В технических науках координаты точек используются для построения и проектирования объектов, моделирования и анализа систем.

Определение точки по координатам является важным инструментом для понимания и анализа пространственных данных. Понимание, как определить точку по координатам, помогает нам лучше взаимодействовать с окружающим миром и применять наши знания в практических ситуациях.

Построение координатной сетки

Давайте рассмотрим базовые принципы построения координатной сетки. Начнем с одномерного пространства, чтобы проиллюстрировать идею. Представьте, что у вас есть прямая линия, на которой вы хотите определить положение точек. Для этого вам понадобится система координат.

Одномерная координатная сетка

Для построения одномерной координатной сетки нужно выбрать и зафиксировать точку, которую мы будем считать нулевой. Эту точку можно обозначить как «начало» или «ноль». Затем, нужно выбрать единицу измерения и прорисовать стрелку, направленную вправо от нулевой точки. Эта стрелка будет служить для определения положения других точек относительно нулевой точки.

Например, если мы выбрали целую единицу измерения и построили стрелку длиной 1, мы можем численно указать расстояние от нулевой точки до любой другой точки на прямой. Если точка находится справа от нулевой точки, мы можем записать ее координату положительным числом, а если она находится слева — отрицательным числом.

Таким образом, мы создали одномерную координатную сетку, которая позволяет нам определить положение точек на прямой линии.

Двумерная координатная сетка

Координатная сетка в двумерном пространстве работает по аналогии с одномерной сеткой, но с двумя осями: горизонтальной и вертикальной. Основным принципом построения двумерной координатной сетки является выбор началочной точки (нулевой точки) и установление направления осей.

Часто выбирают точку с координатами (0, 0) в левом верхнем углу сетки. Ось OX, которая идет горизонтально, направлена вправо от начальной точки, а ось OY, которая идет вертикально, направлена вниз от начальной точки.

Теперь мы можем определить положение любой точки на плоскости, используя пару чисел — координаты X и Y. Координата X определяется расстоянием от начальной точки до точки по горизонтальной оси, а координата Y — расстоянием от начальной точки до точки по вертикальной оси.

Например, если точка находится справа от начальной точки, ее координата X будет положительной. Если она находится слева — отрицательной. Аналогично, если точка находится ниже начальной точки, ее координата Y будет положительной, а если выше — отрицательной.

Таким образом, мы можем использовать двумерную координатную сетку для определения положения точек в двумерном пространстве.

Заключение

Построение координатной сетки является важной задачей в математике и других науках. Она позволяет нам определить положение объектов в пространстве и установить соответствие между точками и их координатами. Одномерная координатная сетка работает на прямой линии, а двумерная — на плоскости. Начальная точка и направление осей определяются при построении сетки.

Перевод между различными системами координат

Перевод между различными системами координат возможен благодаря математическим формулам и алгоритмам. Например, для перевода из прямоугольных координат в полярные координаты используются следующие формулы:

• r = sqrt(x² + y²)
• θ = atan2(y, x)

В прямоугольных координатах точка определяется значениями (x, y), а в полярных координатах — значениями (r, θ). Формулы позволяют перевести значения из одной системы координат в другую.

Кроме прямого перевода между двумя системами координат, также существуют случаи, когда требуется перевод между несколькими системами координат. Например, для перевода из сферических координат в прямоугольные координаты необходимо выполнить последовательные преобразования.

Корректный перевод между различными системами координат имеет большое значение для точного определения положения в пространстве. Он позволяет выполнять различные геометрические вычисления и анализировать данные в нужных единицах измерения. Поэтому разработка и применение алгоритмов для перевода между различными системами координат — важная задача в научных и прикладных исследованиях.