Определение наклонной проведенной из данной точки к прямой и расстояние от точки до прямой: понятие и примеры

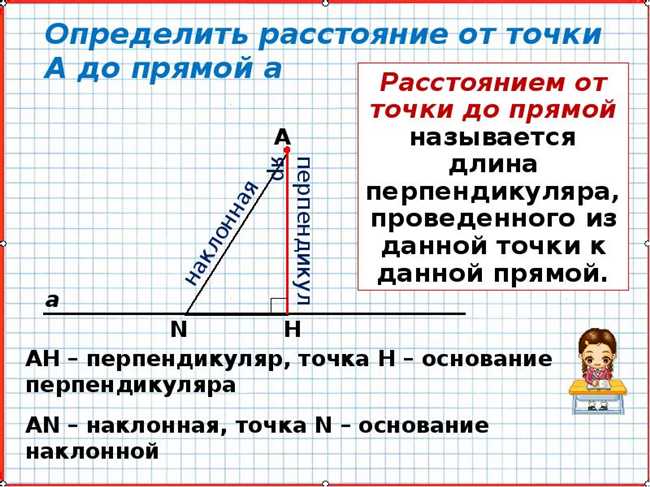
Наклонная проведенная — это прямая линия, которая проходит через данную точку и имеет наклон относительно другой прямой. Определение наклонной проведенной из точки к прямой является важным понятием в геометрии и математике. Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на прямую. Это расстояние может быть вычислено с использованием специальных формул. Понимание концепции наклонной проведенной и расстояния от точки до прямой важно для решения различных задач геометрии, физики, анализа данных и других областей науки. В примерах часто используются задачи о построении перпендикуляров, определении кратчайшего пути или нахождения ближайшей точки к прямой.

Понятие наклонной проведенной из данной точки к прямой

Часто в геометрии возникает задача определить наклонную проведенную из данной точки к данной прямой. Для этого необходимо знание координат точки и уравнение прямой.

Координаты точки состоят из двух чисел, например (x, y). Важно знать, что x определяет положение точки вдоль горизонтальной оси, а y — вдоль вертикальной оси. Координаты прямой представляют собой уравнение, которое содержит коэффициенты и свободный член. Уравнение прямой может быть задано в различных формах, например, в виде y = mx + b, где m — наклон прямой, а b — точка пересечения с осью ординат.

Чтобы найти наклонную проведенную из данной точки к прямой, необходимо использовать следующую формулу: m = (y — y₀) / (x — x₀), где (x₀, y₀) — координаты данной точки. Подставляя значения в формулу, мы получаем наклон этой проведенной.

Например, пусть дана точка A(2, 5) и прямая y = 2x + 3. Чтобы найти наклонную проведенную из точки A к этой прямой, подставим значения в формулу: m = (5 — 3) / (2 — 2) = 2 / 0. Как видно, знаменатель равен нулю, что означает, что наклонная проведенная не существует. Это говорит о том, что точка A не лежит на данной прямой.

Важно понимать, что наклонная проведенная может быть либо положительной, либо отрицательной, либо равной нулю. Положительный наклон означает, что проведенная восходит от точки к прямой, отрицательный наклон — что проведенная нисходит от точки к прямой, а нулевой наклон говорит о том, что проведенная параллельна прямой.

Методы определения наклонной проведенной из данной точки к прямой

Когда речь идет о наклонной, проведенной из данной точки к прямой, существует несколько методов определения.

1. Метод геометрической конструкции

Одним из простых и понятных способов определения наклонной проведенной из точки к прямой является геометрическая конструкция.

1. На координатной плоскости проводится прямая и отмечается точка, из которой надо провести наклонную.
2. Из данной точки проводятся две перпендикулярные прямые к оси абсцисс и оси ординат.
3. Перпендикулярные прямые пересекают основную прямую в двух точках.
4. Требуется соединить исходную точку и точку пересечения перпендикулярных прямых, тем самым получив наклонную проведенную из данной точки к прямой.

2. Метод аналитической геометрии

Другим методом, который широко применяется в аналитической геометрии, является определение уравнения наклонной проведенной из данной точки к прямой.

1. Для начала нужно задать уравнение прямой, относительно которой определяется наклонная. Уравнение прямой может быть дано в виде y = kx + b.
2. Подставляем в уравнение координаты точки, из которой проводится наклонная.
3. С помощью коэффициента k, который определяет наклон прямой, можно определить угол, под которым наклонная пересекает ось абсцисс.
4. Расстояние от точки до прямой может быть определено с помощью формулы |y — kx — b| / √(1 + k^2).

Используя данные методы, можно определить наклонную проведенную из данной точки к прямой и вычислить расстояние от точки до прямой. Это позволяет решать множество геометрических и аналитических задач, связанных с использованием наклонных.

Расстояние от точки до прямой: понятие и формула

Возможно, иногда ты задавался вопросом о том, как определить расстояние от точки до прямой. Не волнуйся, у меня есть ответ для тебя!

Расстояние от точки до прямой — это прямая линия, которая соединяет их и является кратчайшим пути между ними. Важно понимать, что расстояние от точки до прямой может быть измерено только перпендикулярно прямой.

Теперь, когда мы знаем, что такое расстояние от точки до прямой, давай разберем формулу, которая позволяет нам его вычислить.

Для того чтобы вычислить расстояние от точки до прямой, нужно знать координаты точки и уравнение прямой. Формула имеет вид:

d = |Ax + By + C| / √(A^2 + B^2)

Где:

• d — расстояние от точки до прямой
• A и B — коэффициенты уравнения прямой
• C — свободный член уравнения прямой
• x и y — координаты точки

Например, представь, что уравнение прямой имеет вид 3x + 4y — 7 = 0, а точка имеет координаты (2, -1). Тогда мы можем использовать формулу для вычисления расстояния от точки до прямой:

d = |3 * 2 + 4 * (-1) — 7| / √(3^2 + 4^2)

d = |6 — 4 — 7| / √(9 + 16)

d = |(-5)| / √(25)

d = 5 / 5 = 1

Таким образом, расстояние от точки (2, -1) до прямой 3x + 4y — 7 = 0 составляет 1 единицу.

Вот и все! Теперь ты знаешь, как вычислить расстояние от точки до прямой. Используй эту формулу, чтобы решать задачи и находить нужные значения. Удачи в учебе!

Методы нахождения расстояния от точки до прямой

1. Метод расстояния от точки до прямой через координаты

Один из самых простых способов нахождения расстояния от точки до прямой — это использование координат. Представим точку с координатами (x₀, y₀) и уравнение прямой вида ax + by + c = 0. Расстояние между точкой и прямой можно найти по следующей формуле:

d = |ax₀ + by₀ + c| / √(a² + b²)

Где | | обозначает модуль числа. Этот метод основан на формуле для нахождения расстояния между точкой и прямой, которая вытекает из свойства перпендикулярности. Однако, чтобы использовать эту формулу, необходимо знать коэффициенты a, b и c, что может быть неудобно в некоторых случаях.

2. Метод расстояния от точки до прямой через векторы

Еще один метод нахождения расстояния от точки до прямой — это использование векторов. Вектор нормали N к прямой можно найти, зная ее направляющий вектор (a, b). Тогда расстояние d от точки с координатами (x₀, y₀) до прямой будет равно проекции вектора между точкой и прямой на вектор нормали N:

d = |(x₀ - x₁, y₀ - y₁) ⋅ (a, b)| / √(a² + b²)

Здесь (x₁, y₁) — любая точка на прямой. Этот метод основан на свойстве проекций векторов и также позволяет найти расстояние от точки до прямой.

3. Метод перпендикуляров

Самым прямолинейным (простым) методом нахождения расстояния от точки до прямой является способ через построение перпендикуляра. Для этого нужно провести прямую, перпендикулярную данных прямой, через заданную точку. Затем находим точку пересечения этого перпендикуляра с прямой. Расстояние от исходной точки до найденной точки пересечения будет искомым расстоянием.

Однако, метод перпендикуляров требует дополнительных действий, таких как построение прямой и нахождение точки пересечения, поэтому может быть неудобен во многих случаях.

В завершение, выбор метода для нахождения расстояния от точки до прямой зависит от предпочтений и конкретной ситуации. В некоторых случаях, один метод может быть более удобным и эффективным, чем другой. Важно помнить, что математика дает нам множество инструментов для решения различных задач, и выбор оптимального метода — это ключ к успешному решению задачи.

Примеры использования понятия наклонной проведенной из данной точки к прямой и расстояния от точки до прямой

В геометрии, такая наклонная проведенная помогает определить угол между прямой и горизонтальной плоскостью. Например, в архитектуре она используется для построения крыши дома, где наклон крыши должен быть определен для обеспечения слива воды. Также, она помогает визуализировать пересечение линии зрения с определенным объектом, что особенно полезно для фотографов и художников.

В физике, понятие наклонной проведенной используется для изучения движения тела по наклонной плоскости. Например, при расчете скорости скатывания шарика по наклонной поверхности, необходимо знать наклонную проведенную, чтобы определить ускорение и время, необходимые для достижения конечной точки.

Примеры использования понятия наклонной проведенной из данной точки к прямой и расстояния от точки до прямой многочисленны и встречаются во многих областях. От строительства и дизайна до физики и геометрии, эти концепции являются ценным инструментом для решения реальных задач. Имея хорошее понимание этих понятий, мы можем применять их в различных сферах и повышать свою эффективность и точность в решении задач.