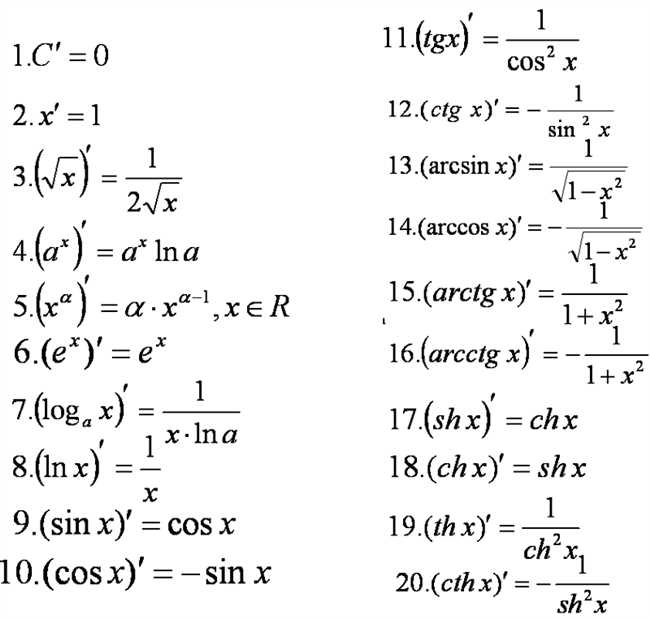
Когда мы изучаем дифференциальное исчисление, мы иногда сталкиваемся с функцией, которая содержит модуль х. Производная от модуля х — это одна из ключевых тем в этой области математики. Определение производной от модуля х довольно простое, но требует внимательности.
Правила дифференцирования модуля х могут быть применены, чтобы упростить вычисление производных функций, содержащих модуль. Эти правила помогают нам найти угловой коэффициент касательной линии к графику функции в определенной точке.
Понимание производной от модуля х является важным шагом в освоении дифференциального исчисления и позволяет нам более глубоко исследовать свойства функций.
Определение производной от модуля х
Модуль числа х обозначается как |х| и всегда возвращает неотрицательное значение, независимо от знака х. Например:
- |2| = 2
- |-3| = 3
Определение производной от модуля числа х зависит от значения х. Рассмотрим два случая:
1. Если х > 0:
Если х положительно, то производная от модуля числа х равна производной самого х. То есть:
d/dx (|x|) = d/dx (x) = 1
Производная постоянна и равна 1 при любом положительном х.
2. Если х < 0:

Если х отрицательно, то производная от модуля числа х равна производной от х, умноженной на -1. То есть:
d/dx (|x|) = d/dx (-x) = -1
Производная постоянна и равна -1 при любом отрицательном х.
Таким образом, производная от модуля числа х равна 1, когда х положительно, и -1, когда х отрицательно. В случае, когда х равно 0, производная от модуля числа х не определена, так как модуль х не является дифференцируемым в точке 0.
Важно понимать, что производная от модуля числа х является разрывной функцией, так как значение производной меняется при переходе через 0. Из-за этого, при работе с модулем числа х необходимо учитывать все три случая: х > 0, х < 0 и х = 0.
Что такое модуль х?

Для положительных чисел модуль равен самому числу, поскольку расстояние от нуля до положительного числа равно самому числу. Например, модуль числа 5 равен 5.
Для отрицательных чисел модуль равен противоположному числу, так как расстояние от нуля до отрицательного числа равно расстоянию от нуля до его противоположного положительного числа. Например, модуль числа -3 равен 3.
Один из способов записи модуля числа x – это выражение |x|. Символы «||» вокруг числа указывают, что мы рассматриваем его модуль.
Вы можете использовать модуль числа в различных математических и физических задачах. Например, если вам нужно найти расстояние между двумя точками на числовой оси, вы можете использовать модуль разности этих двух точек.
Модуль числа также является одной из основных функций в математическом анализе. Он позволяет определить абсолютное значение числа и играет важную роль в решении уравнений и кривых.
Определение производной от модуля х
Модуль числа — это его абсолютное значение, то есть его числовая величина без учета знака. Например, модуль числа -5 равен 5, а модуль числа 3 равен 3.
Для определения производной от модуля х нужно рассмотреть два случая:
- Когда х больше или равно нулю: |х| = х;
- Когда х меньше нуля: |х| = -х.
В первом случае, когда х больше или равно нулю, производная от модуля х равна единице, так как модуль функции в этом случае равен самой функции.
Во втором случае, когда х меньше нуля, производная от модуля х равна отрицательной единице, так как модуль функции в этом случае равен функции, умноженной на -1.
Таким образом, определение производной от модуля х может быть сформулировано следующим образом:
Если х больше или равен нулю, то производная от модуля х равна единице. Если х меньше нуля, то производная от модуля х равна отрицательной единице.
Например, пусть у нас есть функция f(х) = |х|. Если значение х больше или равно нулю, то производная функции f(х) будет равна 1. Если значение х меньше нуля, то производная функции f(х) будет равна -1.
Производная от модуля х играет важную роль в математике и физике, так как позволяет определить градиент функции, который может быть использован для решения различных задач.
Правило дифференцирования функции модуля х
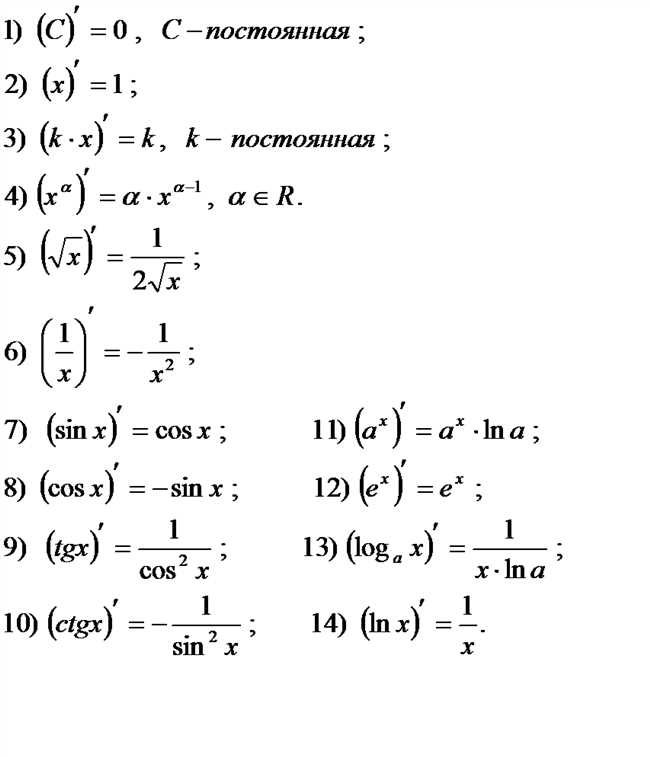
Как и любая другая функция, модуль х может быть дифференцирован. Возможность дифференцирования функции модуля х играет важную роль в анализе и оптимизации задач.
Правило дифференцирования функции модуля х определяется следующим образом:
- Если х > 0, то производная функции модуля х равна 1.
- Если х < 0, то производная функции модуля х равна -1.
- Если х = 0, то производная функции модуля х не существует. В этом случае рассматривается односторонний предел производной, который также равен -1 и 1 соответственно.
Получается, что производная функции модуля х может принимать только два значения: либо 1, либо -1. И это верно независимо от значения х.
Поэтому, если у вас есть функция, содержащая модуль х, вы можете легко найти ее производную, просто заменив модуль х на его производную, равную 1 или -1, в зависимости от знака х.
Применение правила дифференцирования функции модуля х может быть полезным при решении различных математических и инженерных задач. Например, при оптимизации или анализе функций с использованием их производных.
Теперь, когда вы знаете правило дифференцирования функции модуля х, вы можете применять его в своих математических вычислениях и задачах, и это поможет вам получить более точные и эффективные результаты.
Примеры дифференцирования функции модуля х
Пример 1:
Рассмотрим функцию f(x) = |x|. Для того чтобы найти производную этой функции, необходимо рассмотреть два различных случая:
- Если x > 0, то f(x) = x.
- Если x < 0, то f(x) = -x.
Для произвольной точки x_0 > 0, функция f(x) будет равна просто x в окрестности этой точки. Поэтому производная f'(x) для x > 0 будет равна 1.
Аналогично, для произвольной точки x_0 < 0, функция f(x) будет равна просто -x в окрестности этой точки. Поэтому производная f'(x) для x < 0 будет равна -1.
Таким образом, производная функции f(x) = |x| будет равна 1 для x > 0 и -1 для x < 0.
Пример 2:
Рассмотрим функцию g(x) = |2x|. Для того чтобы найти производную этой функции, мы можем воспользоваться правилом дифференцирования произведения:
g'(x) = (2x)’ * |2x| + 2x * (|2x|)’,
где символы ‘ обозначают производные функций.
Так как производная функции 2x равна 2, а производная функции |2x| равна 2 при x > 0 и -2 при x < 0, то производная функции g(x) = |2x| будет равна:
- 2 * |2x| при x > 0.
- -2 * |2x| при x < 0.
Таким образом, производная функции g(x) = |2x| будет различаться для значений x > 0 и x < 0.
График производной от модуля х
График производной от модуля х имеет свои особенности, так как модуль х не является дифференцируемой функцией. Однако, с помощью определенных правил дифференцирования, мы можем получить такой график. Производная от модуля х представляет собой \[f'(x) = \begin{cases} -1, & \text{при } x < 0 \\ 1, & \text{при } x > 0 \end{cases}\]
Таким образом, график производной от модуля х представляет собой две отдельные ветви, расположенные симметрично относительно оси ординат. Она представляет собой горизонтальную прямую при \(x = 0\), а при \(x < 0\) угол наклона функции равен -1, а при \(x > 0\) — 1.
График производной от модуля х является полезным инструментом для изучения поведения функции модуля х и понимания моментов ее изменения скорости. Он помогает понять, когда функция модуля х возрастает или убывает, а также определить точки экстремумов.






