Окружность, проходящая через три точки: верность утверждения и подробный анализ

Верно ли, что через любые три точки проходит не более одной окружности? Этот вопрос волнует не только математиков, но и любознательных людей, ищущих ответы на все загадки и тайны нашего мира. Ответ на этот вопрос скрывается за тонкостями геометрии и постулатами, которые призваны описывать и объяснять законы природы. Математический аспект этой проблемы тоже достаточно сложен, и для полного понимания требует знания определенных теорем и формул. Однако, кратко можно сказать, что через любые три точки на плоскости действительно может проходить только одна окружность. Но чтобы понять, почему это так, нужно погрузиться в мир геометрии и открыть для себя все ее тайны.

О сущности окружности и свойствах трех точек

Вопрос о том, через любые три точки проходит не более одной окружности, имеет однозначный ответ – да, это верно. Это свойство трех точек лежит в основе геометрии и не требует дополнительных условий. Рассмотрим это подробнее.

Свойства окружности

Окружность обладает несколькими важными свойствами, которые помогают понять ее сущность и использовать ее в решении различных задач и проблем. Некоторые из них:

• Радиус и диаметр: Радиус – это расстояние от центра окружности до ее границы, а диаметр – это двукратное расстояние между границами окружности, проходящее через ее центр.
• Определение окружности: Окружность можно определить как множество точек, находящихся на одном расстоянии от центра.
• Длина окружности: Длина окружности может быть вычислена с помощью формулы: длина = 2πr, где r – радиус.
• Тангенциальность: Прямая, касательная к окружности, является перпендикулярной радиусу, опущенному из точки касания.
• Теорема о касательных: Если две касательные к окружности пересекаются, то проходящая через точки пересечения прямая делит диаметр окружности пополам.

Свойство трех точек

Когда мы говорим о свойстве трех точек в контексте окружности, имеется в виду следующее. Если взять любые три точки на плоскости, то существует только одна окружность, проходящая через эти три точки. Такая окружность называется окружностью, проходящей через заданные точки.

Данное свойство легко продемонстрировать на практике. Возьмите лист бумаги и нарисуйте три произвольные точки. Затем, используя циркуль или другой инструмент, нарисуйте окружность, проходящую через эти три точки. Вы увидите, что только одна окружность может быть построена таким образом.

Такое свойство имеет важные применения в геометрии и естественных науках. Например, при решении задач по тригонометрии и геодезии, где требуется нахождение окружности, проходящей через три заданные точки. Также это свойство позволяет нам легко определить окружность по трем точкам, что бывает полезно при анализе и обработке данных.

Заключение

Верно, что через любые три точки проходит не более одной окружности. Это свойство трех точек находится в основе геометрии и является одним из фундаментальных понятий. Зная это свойство, мы можем легко работать с окружностями и применять их в различных областях науки и практики.

Окружность: определение и свойства

Окружность — это плоская геометрическая фигура, состоящая из всех точек, равноудаленных от одной фиксированной точки, называемой центром. Расстояние от центра до точек окружности называется радиусом. Ни для кого не секрет, что окружности окружают нас повсюду — они изображены на планете Земля, в виде колец на пальцах и наручных часах, а также используются в архитектуре и дизайне.

Итак, какие же свойства имеет окружность?

• Окружность имеет бесконечное количество точек. Как уже упоминалось ранее, любая точка на окружности находится на одинаковом расстоянии от центра.
• Диаметр окружности является наибольшим возможным отрезком, соединяющим две точки окружности. Диаметр равен удвоенному радиусу и проходит через центр окружности.
• Окружность может быть определена по трём точкам, не лежащим на одной прямой. Если имеется тройка точек, то существует только одна окружность, которая проходит через все эти точки. Это свойство уникальности окружности делает ее значимой во множестве математических и инженерных задач.
• Угол, образованный двумя хордами (отрезками, соединяющими две точки окружности), равен половине суммы дуг, образованных хордами. Это очень полезное свойство, которое позволяет нам вычислять углы внутри окружности или находить длины дуг.
• Окружность может быть вписана в треугольник и описана вокруг треугольника. Если окружность проходит через каждую из вершин треугольника, она называется описанной окружностью. Если все стороны треугольника касаются окружности, она называется вписанной окружностью. Это свойство окружности открывает возможности для решения многих геометрических задач.

Итак, любимая геометрическая фигура является особой и важной, не только из-за своей уникальности, но и благодаря своим свойствам. Тот факт, что через любые три точки проходит всего одна окружность, является одним из них. В этом и заключается красота и волшебство окружности!

Теорема: через любые три точки проходит не более одной окружности

Давайте рассмотрим эту фундаментальную теорему геометрии более подробно. Она утверждает, что через любые три точки в плоскости можно провести только одну окружность.

Чтобы понять, почему это верно, давайте разберемся с определением окружности. Окружность — это геометрическая фигура, состоящая из всех точек на плоскости, равноудаленных от одной фиксированной точки, называемой центром окружности. То есть, всякий раз, когда три точки находятся на одинаковом расстоянии от одного и того же центра, они образуют окружность.

Окружность определяется тремя точками и может быть рассмотрена как граница множества всех точек, равноудаленных от этих трех точек. Таким образом, если бы через три точки можно было провести более одной окружности, это означало бы, что существует больше одного центра, равноудаленного от данных трех точек.

Но давайте взглянем на это практическим путем. Возьмем для примера три произвольные точки на плоскости и попытаемся провести через них две окружности. Если мы будем двигать центр одной окружности, то уже после некоторого расстояния она перестанет проходить через одну или две из этих трех точек. Получается, что для каждого возможного центра окружности через выбранные три точки, все остальные точки, равноудаленные от этого центра, не будут находиться на одной окружности.

Доказательство теоремы

Верно ли, что через любые три точки проходит не более одной окружности? Давайте разберемся.

Предположим, у нас есть три точки: A, B и C. Мы хотим установить, можно ли провести окружность через эти точки. Воспользуемся свойствами окружностей и треугольников для определения ответа на этот вопрос.

1. Предположим, что через точки A, B и C можно провести окружность.

Это означает, что расстояние от каждой из точек A, B и C до центра окружности одинаково.

2. Для наглядности обозначим центр окружности как O. Тогда расстояние от O до A равно расстоянию от O до B равно расстоянию от O до C.

Мы знаем, что расстояние от точки до центра окружности называется радиусом. Пусть радиус окружности равен r.

3. Согласно свойству равнобедренного треугольника, расстояние от вершины треугольника до середины основания треугольника равно половине длины основания.

Так как у нас есть равнобедренный треугольник OAC, значит расстояние от O до A равно половине отрезка AC.

4. Аналогично, расстояние от O до B равно половине отрезка BC и расстояние от O до C равно половине отрезка AB.

Но мы знаем, что AB = BC = AC, так как у нас есть равносторонний треугольник. Значит, расстояния от O до точек A, B и C равны r/2.

5. Это противоречит нашему изначальному предположению, что расстояние от каждой из точек A, B и C до центра окружности одинаково.

Очевидно, что через точки A, B и C невозможно провести окружность.

Таким образом, мы доказали, что через любые три точки нельзя провести более одной окружности. Это является фундаментальным свойством геометрии и утверждением теории.

Примеры и обоснование теоремы

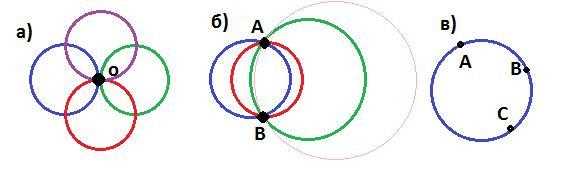
Чтобы понять, каким образом через любые три точки проходит не более одной окружности, рассмотрим следующие примеры и обоснование данной теоремы.

Пример 1:

Пусть имеются три точки A, B и C. Для простоты предположим, что эти точки не лежат на одной прямой. Теперь прокладываем окружность через точки A и B. Это можно сделать бесконечным количеством способов. Затем добавляем третью точку C. Если C лежит на этой окружности, то наша теорема подтверждается. Но что, если C не лежит на данной окружности?

Предположим, что C не лежит на данной окружности. В этом случае, прокладываем окружность через точки B и C. Опять же, есть бесконечное количество способов это сделать. Теперь добавляем четвертую точку D на данной окружности. Если четыре точки A, B, C и D лежат на одной окружности, то наша теорема подтверждается. Однако, если D не лежит на данной окружности, мы можем продолжать этот процесс и добавлять новые окружности через три точки, пока не получим конечную окружность, через которую проходят все наши точки.

Обоснование:

Для обоснования данной теоремы необходимо понимать понятие окружности и ее свойства. Окружность — это геометрическая фигура, состоящая из всех точек, равноудаленных от данной точки, называемой центром окружности. Данное свойство окружности позволяет утверждать, что через любые три точки можно провести только одну окружность.

Это можно объяснить следующим образом: если для трех точек удалось провести окружность, то добавление четвертой точки не будет допускать проведение новой окружности, так как она будет пересекать или касаться предыдущей, и сохранять требуемое свойство окружности — равное расстояние до центра.

Таким образом, приведенные примеры и обоснование теоремы демонстрируют, что через любые три точки проходит не более одной окружности.