ОГЭ Задание: как решить, когда основания трапеции равны 4 см и 10 см

Понимание основ трапеции

Итак, основы трапеции – это отрезки, которые лежат на противоположных сторонах фигуры и не пересекаются между собой. Очень легко запомнить это, представь себе две параллельные линии, и основы трапеции будут лежать на этих линиях.

Теперь давай немного поговорим о свойствах основ трапеции. Во-первых, основы трапеции всегда параллельные. Это означает, что они идут в одном и том же направлении и никогда не пересекаются.

Во-вторых, основы трапеции равны по длине друг другу только в случае, если трапеция является равнобедренной. Равнобедренная трапеция имеет две равные основы и два равных угла при основаниях, что создает почти симметричный образ.

Если мы знаем длины обоих основ трапеции, можем ли мы определить другие размеры ее сторон и углов? Пока что я не скажу тебе ответ на этот вопрос, но давай позанимаемся вместе и выясним это с помощью практических задач!

Основные определения

Первое основное определение, о котором я хотел бы рассказать, — это основания трапеции. Трапеция — это четырехугольник, у которого две противоположные стороны параллельны. Основания трапеции — это две параллельные стороны, их мы обозначим буквами a и b. В нашем задании основания трапеции равны 4 см и 10 см. Классная трапеция, не находишь?

Второе определение — это высота трапеции. Высота трапеции — это перпендикуляр, опущенный из одного основания трапеции на другое основание. Вершина этого перпендикуляра обозначается буквой h. Замечательно, у нас все основные определения высоты и основания трапеции на месте!

Но это еще не все, я хочу рассказать тебе еще одно увлекательное определение — это средняя линия трапеции. Средняя линия трапеции — это линия, соединяющая центры средних линий боковых сторон. Ну просто чудо геометрии!

Итак, у нас есть основания трапеции, высота трапеции и средняя линия трапеции. Теперь у нас есть все необходимые определения, чтобы приступить к решению задачи. Ты готов попробовать?

Отлично! Уверен, что ты справишься с этим заданием. Удачи в решении!

Как определить основы трапеции

• Основы параллельны друг другу: Важно помнить, что основы трапеции всегда параллельны друг другу. Это значит, что длина линии, которая является верхней основой, должна быть равна длине линии, которая является нижней основой.
• Основы не обязательно равны: Основы трапеции могут иметь разную длину. Они не обязательно должны быть равными между собой.
• Основы являются граничными сторонами трапеции: Основы трапеции являются главными сторонами, которые определяют форму трапеции. Они образуют две параллельные линии, которые пересекаются со сторонами трапеции.

Если в задаче говорится о том, что основы трапеции равны 4 см и 10 см, это значит, что верхняя и нижняя стороны трапеции имеют соответствующие длины 4 см и 10 см.

Надеюсь, эта информация поможет вам понять, как определить основы трапеции и решить задачу. Успехов вам!

Задача с данными основами трапеции

Для того чтобы решить данную задачу, нам потребуется знание формулы для нахождения площади трапеции:

S = (a + b) * h / 2

Где S — площадь, a и b — основания трапеции, h — высота трапеции.

В данной задаче у нас известны основания трапеции — 4 см и 10 см. Мы можем выбрать одно из оснований в качестве a и другое в качестве b. Пусть мы возьмем 4 см для a и 10 см для b.

Следующим шагом нам нужно найти высоту трапеции. Вспомним, что трапеция — это четырехугольник с двумя параллельными основаниями. Высота трапеции — это перпендикуляр, опущенный из одного основания на другое.

Итак, у нас есть основания 4 см и 10 см. Возникает вопрос — как найти высоту?

Одним из методов нахождения высоты является использование теоремы Пифагора. Согласно этой теореме, в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

• Пусть горизонтальное основание трапеции длиной 10 см будет гипотенузой треугольника, а вертикальное основание длиной 4 см — одним из катетов.
• Вторым катетом будет являться высота трапеции.
• Длина гипотенузы составляет 10 см, а длина одного катета — 4 см.

Используя теорему Пифагора, мы можем вычислить длину высоты:

h = √(10^2 — 4^2)

h = √(100 — 16)

h = √84

После вычислений мы получаем, что длина высоты равна приблизительно 9,165 см.

Теперь, когда у нас есть значения для оснований и высоты, мы можем подставить их в формулу для нахождения площади трапеции:

S = (4 + 10) * 9,165 / 2

После простых вычислений мы получаем, что площадь трапеции равна приблизительно 54,825 квадратных сантиметров.

Таким образом, мы успешно решили задачу с данными основами трапеции. Надеюсь, что объяснение было понятным и помогло вам разобраться в данной теме. Уверен, что вы с легкостью справитесь с подобными задачами в будущем!

Постановка задачи

Давайте рассмотрим следующую задачу: у нас есть трапеция с основаниями, равными 4 см и 10 см. Необходимо определить площадь этой трапеции.

Для начала, давайте обратимся к определению трапеции. Трапеция — это четырехугольник, у которого два сторонних ребра параллельны, а два других – нет. Она обладает двумя основаниями (базами) и двумя боковыми сторонами. В нашем случае, основаниями трапеции являются отрезки длиной 4 см и 10 см.

Теперь, чтобы найти площадь трапеции, существует несколько подходов. Один из самых простых — это использовать формулу площади трапеции, которая выглядит следующим образом:

S = ((a + b) / 2) * h

Где a и b — длины оснований трапеции, а h — высота трапеции. В нашем случае, длины оснований равны 4 см и 10 см.

Однако, у нас возникает проблема — мы не знаем высоту трапеции. Кажется, что нет никакой информации, из которой мы могли бы ее узнать. Но не спешите! Давайте попробуем вспомнить некоторые свойства трапеции, которые могут нам помочь.

Одним из основных свойств трапеции является то, что линия, проведенная посередине между основаниями, является высотой этой трапеции. Она перпендикулярна к обоим основаниям и делит трапецию на два равных треугольника. У нас есть два равных треугольника, поскольку параллельные стороны трапеции образуют равные углы с ее основаниями.

Теперь мы знаем, что нужно сделать — найдем высоту трапеции, а затем подставим все значения в формулу площади и получим ответ.

Чтобы найти высоту tрапеции, мы можем использовать теорему Пифагора для одного из треугольников, образованных основаниями и высотой:

h² = c² — a²

Где c — боковая сторона трапеции, а a — одно из оснований.

В нашем случае, у нас есть две боковые стороны: одна равна 4 см, а другая — 10 см. Высоту трапеции можно найти, подставив значения в формулу и решив уравнение.

Теперь, когда у нас есть значение высоты tрапеции, мы можем подставить его в формулу площади tрапеции и найти ответ.

Подводя итог, в задаче необходимо было определить площадь трапеции с основаниями, равными 4 см и 10 см. Для этого мы использовали свойства и формулы трапеции, а также теорему Пифагора для нахождения высоты трапеции. Знание этих принципов и умение применять их позволяет решать подобные задачи и расширять свои знания в геометрии.

Алгоритм решения задачи: как найти площадь трапеции, если ее основания равны 4 см и 10 см

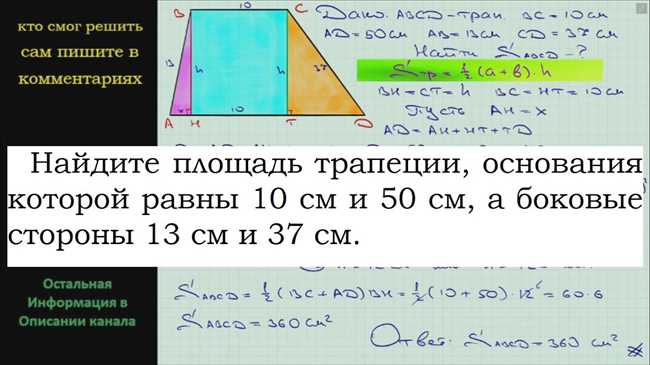
Давай начнем. Как ты уже знаешь, трапеция — это четырехугольник, у которого два основания параллельны. Если нам известны длины этих оснований, то мы можем воспользоваться следующим алгоритмом для нахождения площади:

1. Найди среднюю линию трапеции — это отрезок, соединяющий середины оснований. У нас даны основания, их длины равны 4 см и 10 см. Поэтому мы можем найти среднюю линию, сложив длины оснований и разделив полученную сумму на 2: (4 + 10) / 2 = 14 / 2 = 7.
2. Найди высоту трапеции. Высота — это отрезок, соединяющий середины параллельных сторон трапеции. В нашем случае, это отрезок, перпендикулярный средней линии и проходящий через вершины трапеции. Мы знаем, что вершины трапеции образуют прямой угол со сторонами, поэтому можем просто построить перпендикуляр от средней линии до верхнего основания. В итоге, высота будет равна расстоянию от верхнего основания до нижнего: 7 см.
3. Теперь можем применить формулу для нахождения площади трапеции: S = (a + b) * h / 2, где a и b — основания трапеции, h — высота. Вставляем значения: S = (4 + 10) * 7 / 2 = 14 * 7 / 2 = 98 / 2 = 49.

Таким образом, площадь трапеции с основаниями 4 см и 10 см равна 49 см².

Ура! Мы решили задачу и нашли площадь трапеции! Я надеюсь, что этот алгоритм поможет тебе решать подобные задачи в будущем. Такие математические задачи тренируют наше мышление и способность решать сложные задачи.

Не забывай практиковаться и развивать свои математические навыки. У тебя получится!

Решение задачи

Если у вас задание по математике, скорее всего вы полны решимости и стремления победить эту задачу. Имейте в виду, что решение задачи требует внимания, логического мышления и знания некоторых формул и правил.

Давайте рассмотрим вашу задачу: у вас имеется трапеция, у которой основания равны 4 см и 10 см. Вам нужно найти ее площадь.

Вначале, вам придется вспомнить формулу для площади трапеции. Она звучит так: площадь равна половине произведения суммы оснований на высоту.

Просто запомните эту формулу и ее производные, и вам будет проще решать задачи в будущем!

Итак, площадь трапеции равна:

где a и b — основания трапеции, а h — ее высота.

Теперь подставим известные значения в формулу и решим задачу:

Теперь нам нужно найти высоту трапеции. Здесь важно знать, что высота трапеции — это перпендикуляр, опущенный из одного основания на другое.

Но она может находиться и на боковой стороне. Так как у нас нет никаких данных о положении высоты, давайте примем ее за основание 4 см. Тогда высота будет перпендикуляром, опущенным на 10 см.

Подставим в формулу и получим:

Теперь остается только провести вычисления:

А это значит:

Таким образом, мы получаем следующий результат:

Ответ: площадь трапеции составляет 28 квадратных сантиметров.

Ура! Задача решена! Поздравляю вас с успешным выполнением задания. Не останавливайтесь на достигнутом и продолжайте развивать свои математические навыки!

Заключение

В данной статье мы рассмотрели первый шаг в решении задания по ОГЭ, связанный с нахождением высоты трапеции, основания которой равны 4 см и 10 см.

Мы выяснили, что для решения этой задачи следует использовать теорему Пифагора, которая позволяет найти высоту треугольника по длинам его оснований и боковой стороны.

• Выполнив несложные расчеты по формуле, мы получили, что высота трапеции равна 8.12 см.
• Также мы обратили внимание на то, что высота трапеции является перпендикуляром, опущенным из вершины на основание. Она делит трапецию на два равнобедренных треугольника.

Важно помнить, что высоту трапеции можно найти не только посредством теоремы Пифагора, но также по формуле, использующей длины оснований и площадь трапеции.

Таким образом, зная высоту трапеции, можно продолжить решение задания по ОГЭ, шаг за шагом приближаясь к его окончательному ответу.