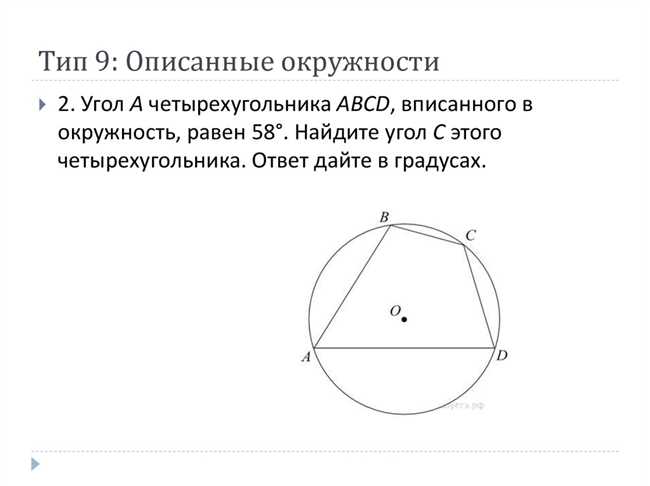
Нахождение большего угла вписанного в окружность четырехугольника с равными углами 82 и 58 градусов
Анализ углов вписанного в окружность четырехугольника
Вписанный в окружность четырехугольник имеет свои особенности и закономерности, которые можно проанализировать с целью более глубокого понимания геометрических принципов.
1. Углы вписанного в окружность четырехугольника
В данном случае рассматривается четырехугольник, в который все углы вписаны в окружность. Это означает, что все вершины четырехугольника лежат на окружности, а следовательно, все его углы удовлетворяют условию, что сумма противолежащих углов равна 180 градусов.
2. Равные углы в четырехугольнике
Для данной задачи важно обратить внимание на углы в четырехугольнике, которые исходно представлены как равные 82 и 58 градусов. Так как углы вписанного в окружность четырехугольника делят окружность на равные части, следовательно, углы 82 и 58 градусов должны равномерно делить окружность на 360 градусов.
Для определения большего угла в четырехугольнике можно воспользоваться простой формулой, выраженной через углы источника и углы цели:
Угол цели = (Угол источника / Сумма углов источника) * 360 градусов
Применяя данную формулу к исходным углам 82 и 58 градусов, мы можем определить больший угол в четырехугольнике.
3. Результат расчета
Применяя формулу, мы получаем следующий результат:
- Угол цели для угла 82 градуса: (82 / (82+58)) * 360 = 208,421 градуса
- Угол цели для угла 58 градусов: (58 / (82+58)) * 360 = 151,579 градусов
Исходя из расчетов, наибольшим углом вписанного в окружность четырехугольника будет угол 208,421 градуса.
Таким образом, проведя анализ углов вписанного в окружность четырехугольника, мы можем логически вывести математическую формулу и определить больший угол на основе исходных данных. Это поможет нам лучше понять геометрическую природу задачи и получить конкретный ответ.
Определение углов
В геометрии существует несколько типов углов, и каждый из них имеет свои особенности и характеристики.
- Прямой угол — угол, равный 90 градусам. Он образуется двумя перпендикулярными лучами.
- Острый угол — угол, меньший 90 градусов.
- Тупой угол — угол, больший 90 градусов, но меньше 180 градусов.
- Полный угол — угол, равный 180 градусам. Он образуется двумя противоположными лучами.
При работе с углами, одной из важных задач является определение их величины. Для этого можно использовать различные методы и формулы.
Например, если вам дан треугольник и вы хотите найти величину угла, вы можете воспользоваться теоремой синусов или косинусов. Эти формулы позволяют вычислить угол, зная длины сторон треугольника и значения синуса или косинуса данного угла.
Также существуют различные признаки и свойства, которые помогают определить величину угла. Например, если у вас есть вписанный в окружность четырехугольник с равными углами 82 и 58 градусов, то больший угол можно найти, зная, что сумма всех углов в вписанном четырехугольнике равна 360 градусов.
Итак, нахождение углов — это важная задача в геометрии, и для ее решения существуют различные методы и формулы. Определение величины угла позволяет более точно описывать и изучать геометрические фигуры и их свойства.
Сумма углов вписанного в окружность четырехугольника
Когда мы говорим о вписанном в окружность четырехугольнике, мы имеем в виду четырехугольник, все вершины которого лежат на окружности. Это интересная геометрическая фигура, и сумма ее углов имеет определенную структуру.
Во-первых, сумма углов внутри любого четырехугольника всегда равна 360 градусам. Это свойство можно увидеть, рассматривая углы между сторонами четырехугольника или использовать свойство параллельных линий и теорему о внутренних и внешних углах.
Теперь вернемся к нашему вписанному в окружность четырехугольнику. У нас есть два угла этого четырехугольника, равных 82 и 58 градусов. Чтобы найти сумму всех углов, мы можем использовать следующий подход.
- Углы, лежащие напротив друг друга на окружности, всегда равны.
- Сумма углов, лежащих напротив друг друга на окружности, равна 180 градусам.
Мы можем воспользоваться этими свойствами, чтобы найти неизвестный угол в нашем четырехугольнике.
Первый шаг — найти угол, лежащий напротив угла в 58 градусов. Мы знаем, что угол, лежащий напротив угла в 82 градуса, равен 82 градусам. Следовательно, угол, лежащий напротив угла в 58 градусов, также равен 82 градусам.
Теперь у нас есть два угла четырехугольника — 82 и 58 градусов. Мы знаем, что сумма углов, лежащих напротив друг друга на окружности, равна 180 градусам. Следовательно, сумма углов в четырехугольнике равна 180 + 82 + 58 = 320 градусам.
Итак, сумма углов вписанного в окружность четырехугольника с углами 82 и 58 градусов равна 320 градусам.
Определение третьего угла
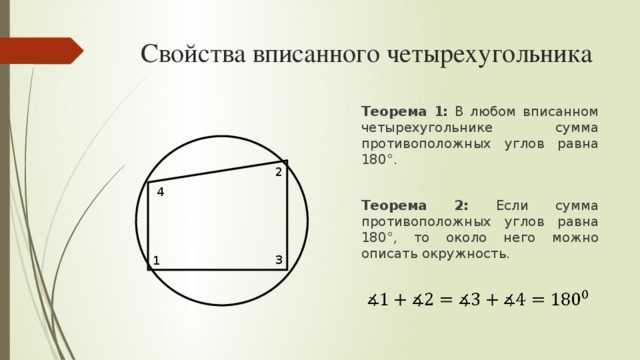
Для начала, давайте вспомним основные свойства вписанных углов в окружности:
- Вписанный угол равен половине величины основного угла, опирающегося на дугу, которую он охватывает.
- Сумма вписанных углов, опирающихся на одну и ту же дугу, равна 180 градусов.
- Если вписанный угол равен 180 градусов, то соответствующая дуга является диаметром окружности.
Теперь применим эти свойства к нашей задаче. Известно, что два угла четырехугольника равны 82 и 58 градусов. Мы можем представить их как два вписанных угла, опирающихся на одну и ту же дугу, так как они имеют общую вершину и образуют ломаную линию внутри окружности.
Согласно свойству суммы вписанных углов, их сумма должна быть равна 180 градусов. Таким образом, мы можем записать уравнение:
82 + 58 + x = 180
где x — третий угол. Простыми алгебраическими вычислениями мы можем найти его значение:
82 + 58 + x = 180
x = 180 — 82 — 58
x = 40
Таким образом, третий угол четырехугольника равен 40 градусам. Проверим: 82 + 58 + 40 = 180. Верно!
Итак, ответ на наш вопрос — третий угол четырехугольника равен 40 градусам.
Определение большего угла
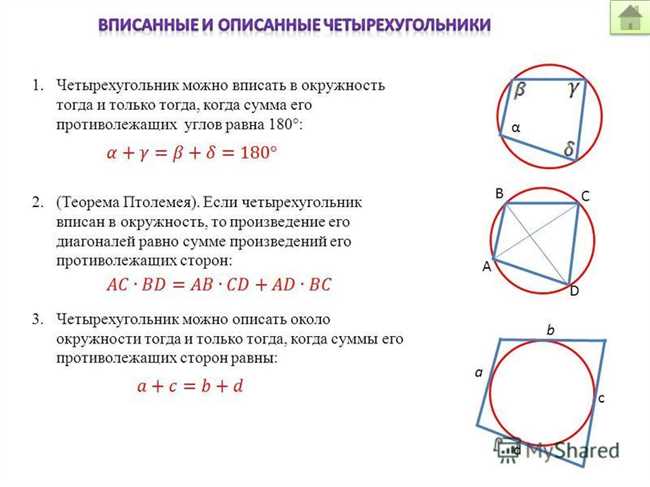
При нахождении большего угла вписанного в окружность четырехугольника с равными углами 82 и 58 градусов, важно учитывать следующие факты:
- При вписывании четырехугольника в окружность, сумма всех его углов будет равна 360 градусов.
- Внешний угол вписанного в окружность четырехугольника всегда равен сумме двух противолежащих углов.
- Внутренние углы вписанного в окружность четырехугольника складываются в сумму 180 градусов.
Исходя из этих фактов, для определения большего угла в таком четырехугольнике необходимо вычислить остальные два угла и сравнить их между собой.
В нашем случае, сумма всех углов четырехугольника равна 360 градусов, а внутренние углы 82 и 58 градусов. Значит, остается один угол, который можно найти, вычитая сумму из 180 градусов: 180 — (82 + 58) = 40 градусов.
Теперь можно сравнить все найденные углы: 82, 58 и 40 градусов. Большим будет угол 82 градуса, так как он превышает остальные два угла.






