Методы и примеры расчета наименьшего общего кратного (НОК)

Содержание

Методы нахождения наименьшего общего кратного
Методы факторизации чисел
1. Метод простой делимости
2. Метод квадратного корня
3. Метод раскладывания на множители
Заключение
Метод перебора делителей
Метод пошагового умножения
Примеры расчета
Пример 1:
Пример 2:
Пример 3:

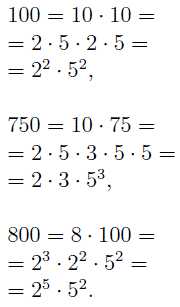
Когда мы работаем с дробями и числами, мы иногда сталкиваемся с необходимостью найти их наименьшее общее кратное (НОК). НОК — это наименьшее число, которое делится на все заданные числа без остатка. Существует несколько методов для нахождения НОК чисел. Один из них — метод простых множителей, который основан на разложении чисел на простые множители и выборе наибольших степеней простых чисел, встречающихся в разложениях. Другой метод включает поиск НОК через общие кратности двух чисел. Если у нас есть только два числа, мы можем использовать их произведение, поделенное на их наибольший общий делитель (НОД), чтобы найти НОК. Давайте рассмотрим некоторые примеры расчета НОК, чтобы более полно ознакомиться с этим процессом.

Методы нахождения наименьшего общего кратного

На самом деле, существует несколько методов для нахождения НОК. Давайте рассмотрим несколько из них и посмотрим, как они работают:

Метод разложения на простые множители: Этот метод основан на использовании разложения чисел на их простые множители. Сначала разложите каждое число на простые множители и найдите максимальное количество повторяющихся простых множителей для каждого числа. Затем перемножьте эти простые множители вместе, чтобы получить НОК.
Метод последовательного увеличения: Этот метод основан на последовательном увеличении числа, начиная с наибольшего из заданных чисел, пока не будет найдено число, которое делится на все заданные числа без остатка. Найденное число будет НОК.
Метод использования таблицы: В этом методе создается таблица, в которой в первом столбце перечислены заданные числа, а в остальных столбцах перечислены их кратные значения. Затем ищется первое число, которое встречается во всех столбцах, и оно будет НОК.

Теперь давайте посмотрим на примеры расчета НОК с помощью этих методов:

Пример 1: Найдем НОК чисел 12 и 18 с помощью метода разложения на простые множители.

Число 12 можно разложить на простые множители как 2 * 2 * 3, а число 18 как 2 * 3 * 3. Максимальные повторяющиеся простые множители для числа 12 – 2, 2 и 3, а для числа 18 – 2 и 3. Перемножим эти простые множители вместе: 2 * 2 * 3 * 3 = 36. Таким образом, НОК чисел 12 и 18 равно 36.

Пример 2: Найдем НОК чисел 5, 8 и 10 с помощью метода последовательного увеличения.

Начнем с числа 10, так как оно является наибольшим из заданных чисел. Увеличивая его последовательно на 10 (потому что это самый большой из заданных чисел), мы можем увидеть, что 10, 20, 30 и 40 не делятся на 5 и 8 без остатка. Но когда мы достигаем числа 50, мы видим, что оно делится и на 5, и на 8 без остатка. Таким образом, НОК чисел 5, 8 и 10 равно 50.

Пример 3: Найдем НОК чисел 4, 6 и 8 с помощью метода использования таблицы.

Числа	Кратные значения
4	4, 8, 12, 16, 20, 24, 28, 32, 36, …
6	6, 12, 18, 24, 30, 36, 42, 48, 54, …
8	8, 16, 24, 32, 40, 48, 56, 64, 72, …

Таким образом, НОК чисел 4, 6 и 8 равно 24, так как это первое число, которое встречается во всех столбцах таблицы.

Важно помнить, что нахождение НОК трех и более чисел может потребовать использования более сложных методов, таких как расширенный алгоритм Евклида или решето Эратосфена. Однако описанные выше методы хорошо подходят для нахождения НОК двух чисел и обеспечивают нам надежные результаты.

Методы факторизации чисел

Существует несколько методов факторизации чисел, каждый из которых может быть применим в различных ситуациях. Рассмотрим некоторые из них.

1. Метод простой делимости

Самый простой и широко используемый метод факторизации чисел – это метод простой делимости. Он основывается на проверке делимости числа на простые числа.

Интересно: Важные достоинства эмалированных дверей: красота, устойчивость, долговечность

Шаги этого метода следующие:

Выбрать первое простое число, например, 2.
Проверить, делится ли исходное число на данное простое число без остатка.
Если делится, записать это простое число в список множителей и поделить исходное число на него.
Если не делится, выбрать следующее простое число и повторить шаги 2-3.
Продолжать процесс до тех пор, пока исходное число не станет единицей.

Например, для числа 24 следующая последовательность будет выглядеть так:

24 делим на 2 без остатка. Добавляем 2 в список множителей и делим число на 2, получаем 12.
12 делим на 2 без остатка. Добавляем 2 в список множителей и делим число на 2, получаем 6.
6 не делится на 2 без остатка, пробуем следующее простое число – 3.
6 делим на 3 без остатка. Добавляем 3 в список множителей и делим число на 3, получаем 2.
2 – простое число, делим на него без остатка. Добавляем 2 в список множителей и получаем единицу.

В результате получаем, что 24 = 2 * 2 * 2 * 3 = 2³ * 3.

2. Метод квадратного корня

Для больших чисел, метод простой делимости может быть очень трудоемким. В таких случаях можно применить метод квадратного корня.

Шаги этого метода следующие:

Найти квадратный корень исходного числа.
Начать делить исходное число на простые числа, начиная с 2, и проверять на делимость.
Если число делится, записать множитель и поделить исходное число на него.
Повторять шаги 2-3 до тех пор, пока делитель не станет больше квадратного корня исходного числа.

Например, для числа 100, квадратный корень из которого равен 10, можно применить следующий алгоритм:

Проверяем делимость на 2 – 100 не делится на 2.
Проверяем делимость на 3 – 100 не делится на 3.
Проверяем делимость на 5 – 100 делится на 5. Записываем множитель 5 и делим число на 5, получаем 20.
Проверяем делимость на 7 – 20 не делится на 7.
Проверяем делимость на 11 – 20 не делится на 11.
…

В результате получаем, что 100 = 2 * 2 * 5 * 5 = 2² * 5².

3. Метод раскладывания на множители

Если числа не слишком большие, можно применить метод раскладывания числа на множители. В этом методе мы пытаемся разложить число на произведение множителей, выраженных в пределах определенного диапазона.

Шаги этого метода следующие:

Выбрать диапазон множителей, например, от 2 до квадратного корня из исходного числа.
Начинать с минимального множителя и проверять делится ли исходное число на данный множитель без остатка.
Если число делится, записать множитель и поделить исходное число на него.
Продолжать проверять делитель на делимость и повторять шаг 3 в диапазоне от минимального до квадратного корня из исходного числа.

Например, для числа 30 можно применить следующий алгоритм:

Проверяем делимость на 2 – 30 делится на 2. Записываем 2 в список множителей и делим число на 2, получаем 15.
Проверяем делимость на 3 – 15 делится на 3. Записываем 3 в список множителей и делим число на 3, получаем 5.
Проверяем делимость на 4 – 5 не делится на 4.
Проверяем делимость на 5 – 5 делится на 5. Записываем 5 в список множителей и делим число на 5, получаем 1.

В результате получаем, что 30 = 2 * 3 * 5.

Заключение

В данной статье мы рассмотрели три основных метода факторизации чисел: метод простой делимости, метод квадратного корня и метод раскладывания на множители. Каждый из них имеет свои преимущества и может быть полезен в различных ситуациях. От выбора метода будет зависеть скорость и удобство работы с числами.

Метод перебора делителей

Суть метода перебора делителей заключается в поиске всех делителей каждого числа и выборе наименьшего общего кратного из найденных делителей.

Давай рассмотрим пример. Пусть нам нужно найти НОК чисел 12 и 15.

Для начала найдем все делители каждого числа:

Делители числа 12: 1, 2, 3, 4, 6, 12
Делители числа 15: 1, 3, 5, 15

Теперь выберем наименьший общий делитель из этих двух списков: 1.

Значит, НОК чисел 12 и 15 равно 1.

Теперь давай подумаем о более сложном примере. Пусть нам нужно найти НОК чисел 18, 24 и 36.

Находим все делители каждого числа:

Делители числа 18: 1, 2, 3, 6, 9, 18
Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24
Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

Выбираем наименьший общий делитель: 1.

Значит, НОК чисел 18, 24 и 36 также равно 1.

Обрати внимание, что метод перебора делителей требует нахождения всех делителей каждого числа, что может быть неэффективным при больших значениях чисел. Тем не менее, этот метод остается простым и понятным для понимания. Он может быть полезен в тех случаях, когда нужно найти НОК небольшого набора чисел, или при использовании в качестве вспомогательного метода в сложных задачах.

В итоге, метод перебора делителей — один из доступных способов нахождения наименьшего общего кратного чисел. Он может быть полезен в различных ситуациях, особенно в случае с небольшими числами.

Метод пошагового умножения

Прежде всего, давайте помним, что НОК двух чисел — это наименьшее положительное число, которое делится без остатка на эти два числа. Зная это, мы можем приступить к пошаговому умножению.

Давайте рассмотрим пример нахождения НОК для чисел 6 и 8 с использованием метода пошагового умножения:

Шаг	Число	Кратность	Общая кратность
1	6	1	6
2	8	1	24
3	6	2	24

Здесь мы начинаем с первого числа 6 и увеличиваем его на 6 на каждом шаге. При каждом шаге мы проверяем, является ли текущее число кратным второму числу 8. Когда мы достигаем числа 24, мы видим, что и 6, и 8 делятся на него без остатка. Таким образом, 24 является наименьшим общим кратным чисел 6 и 8.

Использование метода пошагового умножения позволяет нам систематически увеличивать число и проверять его кратность до тех пор, пока мы не найдем НОК. Этот метод может быть полезен, особенно когда числа, для которых мы ищем НОК, не слишком большие.

Вы также можете применять метод пошагового умножения для большего числа чисел, просто продолжив цикл умножения и проверки на кратность для каждого нового числа, пока не найдется общее кратное для всех чисел.

Примеры расчета

На практике расчет НОК часто используется для решения различных математических задач. Ниже приведены несколько примеров, демонстрирующих методику расчета наименьшего общего кратного.