Медиана, биссектриса и высота треугольника — геометрические понятия и свойства: что означают эти термины и как они влияют на строение треугольника?

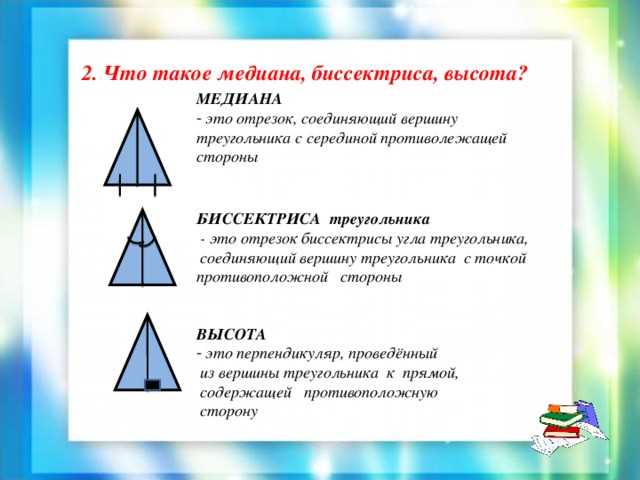
Медиана, биссектриса и высота треугольника — это основные геометрические понятия, которые относятся к его сторонам и углам. Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Она делит медиану на две равные части и пересекается с противоположной стороной под прямым углом. Биссектриса — это отрезок, который делит угол треугольника на два равных угла. Она пересекает противоположную сторону треугольника под прямым углом и проходит через его вершину. Высота треугольника — это отрезок, соединяющий вершину треугольника с противоположной стороной и проходящий под прямым углом к этой стороне. Медиана, биссектриса и высота имеют свои уникальные свойства и играют важную роль в геометрии треугольника.

Определение и свойства медианы треугольника

Давайте рассмотрим это более подробно. Представьте треугольник ABC, где A, B и C — вершины треугольника, а BC, AC и AB — стороны треугольника. Медиана треугольника BC — это отрезок, который соединяет вершину A с серединой стороны BC.

Основное свойство медианы треугольника заключается в том, что она делит этот треугольник на два равных по площади треугольника. Другими словами, площадь треугольника ABC равна сумме площадей треугольников, образованных медианой.

Медианы треугольника также имеют свою точку пересечения, называемую центром масс. Центр масс находится на трети пути каждой из медиан и является точкой, где силы тяжести треугольника сосредоточены.

Существуют некоторые интересные свойства медиан треугольника:

• Медианы треугольника пересекаются в одной точке, называемой центром масс или барицентром треугольника.
• Медиана, проведенная из вершины треугольника, делит ее на две части, длины которых обратно пропорциональны длинам противолежащих сторон.
• Медиана треугольника является самым коротким отрезком, соединяющим вершину треугольника с противоположной стороной.

Теперь, с учетом этих свойств, мы сможем легко использовать медианы для решения геометрических задач, связанных с треугольниками. Они помогут нам найти центр масс треугольника, разделить его на две равные части и многое другое.

Определение медианы

Медианы играют важную роль в геометрии треугольника. Они пересекаются в одной общей точке, которая называется центром тяжести треугольника. Центр тяжести — это точка, в которой сосредоточена масса треугольника, и он находится на 2/3 от каждой медианы. Это значит, что если вы подвесите треугольник за каждую его медиану, то он будет находиться в равновесии.

По свойству медиан, их длины могут быть использованы для нахождения площади треугольника по формуле: площадь треугольника равна половине произведения длин любой медианы на перпендикуляр, опущенный из вершины, к которой примыкает медиана, на эту медиану.

Пример:

Рассмотрим треугольник ABC со сторонами a, b и c. Медианы треугольника обозначим как m_a, m_b, и m_c. Пусть p — полупериметр треугольника, то есть p = (a + b + c)/2

• Длина медианы m_a равна 1/2 * √(2b² + 2c² — a²)
• Длина медианы m_b равна 1/2 * √(2a² + 2c² — b²)
• Длина медианы m_c равна 1/2 * √(2a² + 2b² — c²)

Кроме того, медианы треугольника можно использовать для нахождения высот. Высоты треугольника — это перпендикуляры, опущенные из вершин к противолежащим сторонам. Медиана также является основанием для высоты треугольника, и длина высоты может быть найдена с использованием теоремы Пифагора.

Таким образом, медианы играют важную роль в геометрии треугольника, устанавливая связь между вершинами и центром тяжести треугольника. Они также помогают находить площадь треугольника и длины его высот.

Свойства медианы

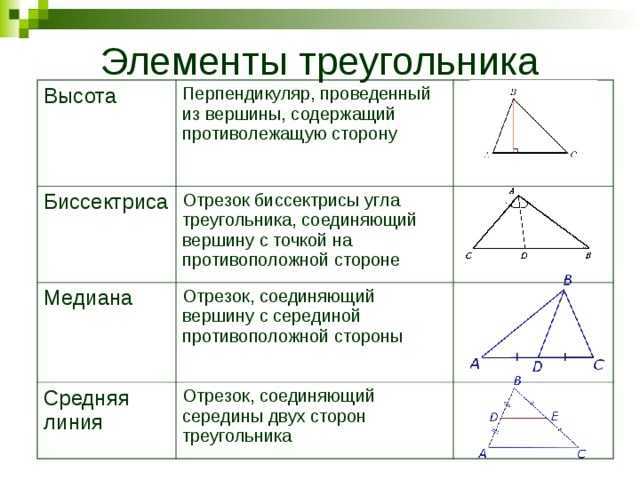
Медианы имеют ряд свойств, которые полезно знать:

• 1. Медиана является линией симметрии. Если треугольник симметричный относительно медианы, то длина медианы будет равна половине периметра треугольника.
• 2. Медиана делит треугольник на два равновеликих треугольника. Если отметить точку пересечения медиан с противоположной стороной треугольника, то каждый из этих треугольников будет иметь одинаковую площадь.
• 3. Медиана и высота могут иметь одинаковую длину в некоторых случаях. Это происходит только в равнобедренных треугольниках, где медиана, проведенная из вершины основания к основанию, является одновременно и высотой.

Медианы треугольника также используются при решении задач и вычислении различных параметров треугольника, например, его площади или радиуса вписанной окружности.

Важно помнить, что медиана – это геометрический конструкт, а не свойство самого треугольника. Она зависит от расположения вершин треугольника и проводится из каждой вершины к середине противоположной стороны. При изменении положения вершин треугольника медиана также будет меняться.

Определение и свойства биссектрисы треугольника

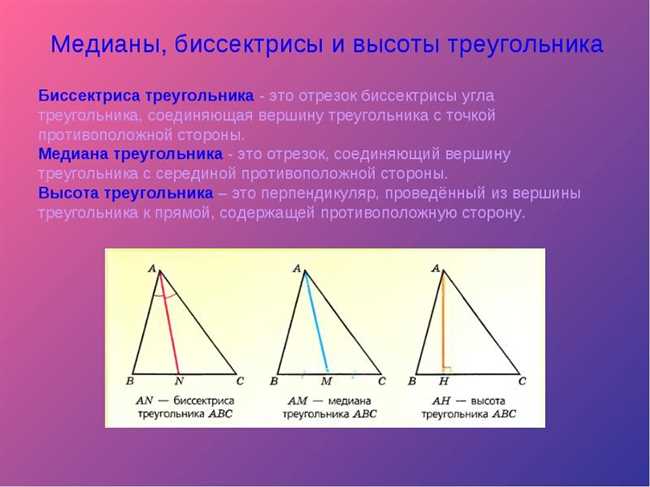
Биссектриса является важным элементом треугольника, так как она имеет несколько свойств и применений:

• Деление сторон: Биссектриса треугольника делит противоположную ей сторону на две отрезка пропорциональных длин. Отношение длин этих отрезков равно отношению длин двух других сторон треугольника, которые соединены с вершиной данного угла.
• Связь с другими элементами треугольника: Биссектриса треугольника перпендикулярна его высоте и пересекается с медианой в одной точке, называемой центром биссектрис треугольника.
• Угол между биссектрисой и противоположной стороной: Угол между биссектрисой и противоположной ей стороной треугольника равен половине суммы двух других углов этого треугольника.

Биссектрисы треугольника играют важную роль в различных геометрических и тригонометрических задачах. Они позволяют определить точки пересечения медиан, провести вписанную окружность и решить другие задачи, связанные с углами и сторонами треугольника.

Понимание определения и свойств биссектрисы треугольника является важным для решения задач в геометрии и может быть полезно при изучении других разделов математики, где треугольники играют важную роль.

Определение биссектрисы

Представь себе треугольник с одним из его углов внизу. Теперь визуализируй линию, которая идет от вершины этого угла и делит его пополам. Вот эта линия и будет биссектрисой.

Биссектриса имеет ряд уникальных свойств и играет важную роль в геометрии:

• Биссектриса треугольника равноудалена от боковых сторон этого угла. Иными словами, расстояние от биссектрисы до каждой из сторон угла одинаково.
• Биссектрисы всех трех углов одного и того же треугольника пересекаются в одной точке, которая называется центром вписанной окружности. Это важное свойство используется во многих задачах геометрии.
• Биссектрисы могут служить основой для построения других фигур и вычислений, например, чтобы найти расстояние от биссектрисы до точки на боковой стороне треугольника или найти углы треугольника, зная величины других углов.

Таким образом, биссектриса является важным понятием в геометрии и имеет множество применений и свойств. Она помогает нам понять и изучать треугольники, исследовать их углы и строить другие фигуры.

Свойства биссектрисы

• Биссектриса делит противоположную сторону в отношении, равном отношению двух остальных сторон угла. Это свойство называется теоремой о биссектрисе. Если AC и BC — две стороны угла ABC, а BD — биссектриса этого угла, то отношение длин отрезков AD и CD равно отношению длин сторон AB и BC: AD/CD=AB/BC.
• Биссектриса является высотой в случае равных сторон угла. Если AB и AC — две равные стороны угла ABC, а BD — биссектриса этого угла, то BD одновременно является и высотой этого угла. Это свойство позволяет найти высоту угла, зная его биссектрису.
• Биссектриса перпендикулярна прямой, проходящей через середину противолежащей стороны и точку пересечения других двух биссектрис. Если BD и BE — биссектрисы угла ABC, а M — середина стороны AC, то прямые BD и BE перпендикулярны. Это свойство позволяет находить перпендикулярные прямые, проходящие через биссектрисы угла.

Таким образом, свойства биссектрис позволяют использовать их в различных геометрических задачах и вычислениях. Знание этих свойств поможет легче разобраться в структуре треугольника и использовать его особенности в доказательствах и решении задач.