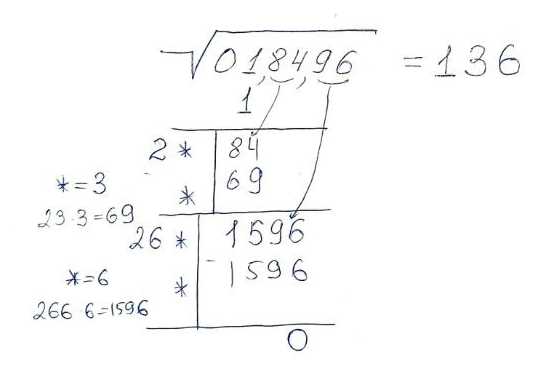
Корень из двух является одной из самых известных и одновременно загадочных математических констант. Он представляет собой число, которое при возведении в квадрат равно двум. Однако, попытка выразить это число в десятичной форме оказывается бесконечной и не поддающейся точному выражению. При округлении корня из двух до определенного количества знаков после запятой, мы все равно получим только приближенное значение. Эта неразрешимость обусловлена особенностями десятичной системы, которая имеет конечное число цифр, но неспособна выразить некоторые числа бесконечной длины. Таким образом, корень из двух остается неразрешимой и загадочной константой в математике.
Природа и свойства корня из двух
Свойства корня из двух можно разделить на теоретические и практические аспекты. Теоретически, корень из двух является иррациональным числом, что означает, что его не может быть точно представлено в виде десятичной дроби или отношения двух целых чисел. Это связано с тем, что квадрат иррационального числа не может быть целым числом.
Практически, это означает, что мы не можем представить корень из двух в виде конечной десятичной дроби. Результатом возведения этого числа в квадрат будет приближенное значение 2, но никогда точно 2. Допустим, что мы представляем корень из двух в виде десятичной дроби 1,41421356… При возведении этой дроби в квадрат получим приближенное значение 1,99999994… Для получения большей точности, нам потребуется бесконечное количество знаков после запятой.
Таблица с историческими приближениями корня из двух:
| Приближение | Количество знаков после запятой | Погрешность |
|---|---|---|
| 1,4 | 1 | 0,2 |
| 1,41 | 2 | 0,01 |
| 1,414 | 3 | 0,001 |
| 1,4142 | 4 | 0,0001 |
Интересно, что корень из двух появился в древнем мире задолго до появления понятия иррациональных чисел. В Древней Греции математики сталкивались с проблемой несоответствия между длиной диагонали квадрата и его стороной. Они уже понимали, что это число не может быть выражено целым или дробным числом, и олицетворяли его символом.
Свойства корня из двух делают его уникальным и интересным для математиков и ученых. Оно представляет собой числовой символический объект, который раскрывает глубину и неразрешимость некоторых математических проблем. Корень из двух неразделим с помощью простых чиселых отношений и остается загадкой, подобно многим другим феноменам в нашем мире.
Таким образом, корень из двух обладает уникальными свойствами, которые делают его неразрешимым в форме десятичной дроби. Понимание и признание этой уникальности позволяет нам продолжать исследовать и открывать новые грани математики. Возможно, в будущем мы найдем новые подходы к представлению корня из двух, но пока мы можем лишь наслаждаться его загадочной и красивой природой.
Ограничения десятичной системы
Однако, несмотря на все преимущества десятичной системы, она имеет свои ограничения. Одним из таких ограничений является невозможность точно выразить некоторые числа, включая корень из двух, в десятичной форме.
Корень из двух является иррациональным числом, что означает, что его десятичная запись не ограничена длиной и не может быть представлена в виде десятичной дроби или конечного числа. В десятичной системе, мы всегда сталкиваемся с ограничением конечного числа десятичных разрядов, поэтому невозможно точно выразить корень из двух в десятичной форме.
Такая невозможность точного выражения корня из двух в десятичной системе создает определенные проблемы при решении математических задач, особенно в областях, связанных с геометрией, физикой, инженерией и компьютерной наукой. В таких областях требуется высокая точность и невозможность точного представления корня из двух в десятичной форме может усложнить вычисления и привести к неточным результатам.
Необходимость точного представления корня из двух и других иррациональных чисел привела к использованию других систем счисления, таких как десятичная система с увеличенной точностью, двоичная система, которая используется в компьютере и позволяет точно представить корень из двух в виде бесконечной двоичной дроби.
Таким образом, ограничения десятичной системы счисления и невозможность точного выражения корня из двух в десятичной форме подтверждают, что существует много других систем счисления, которые могут быть более эффективными и точными в различных областях науки и технологии.
Результаты приближенных вычислений
Одной из причин, почему приближенные вычисления не дают абсолютно точных результатов, является ограниченность чисел, которые можно представить в компьютере. Компьютеры используют двоичную систему счисления, в которой числа представляются в виде последовательности единиц и нулей. Это позволяет компьютерам обрабатывать числа очень быстро, но также ограничивает их точность.
Еще одной причиной неточных результатов являются методы округления, используемые при выполнении вычислений. Во многих случаях невозможно точно представить бесконечные иррациональные числа, такие как число π или корень квадратный из двух, в десятичной форме. Вместо этого используются приближенные значения, которые соответствуют определенному количеству знаков после запятой.
Когда мы вычисляем корень из двух, мы получаем бесконечную десятичную дробь, которая не может быть представлена точно в десятичной форме. Мы можем приблизительно вычислить значение корня из двух, используя различные методы, такие как метод Ньютона или метод деления пополам. Однако, даже с использованием этих методов, мы не сможем получить абсолютно точный результат.
Таким образом, приближенные вычисления дают нам результаты, которые достаточно близки к точным значениям, но не являются абсолютно точными. Это необходимо учитывать при использовании результатов приближенных вычислений, особенно в задачах, где точность критически важна.
Альтернативные способы представления корня из двух

Один из таких способов — использование десятичных десятичных дробей. Например, можно представить корень из двух как 1.41 или 1.414, где число цифр после запятой определяет точность приближения. Чем больше цифр, тем ближе будет значение к истинному корню из двух.
Другой способ — использование бесконечных десятичных дробей. В данном случае корень из двух записывается как бесконечная десятичная дробь «1.41421356…». Это число не имеет точного окончания и продолжает бесконечно повторяться, но является приближенным значением корня из двух.
Однако, несмотря на приближенное представление корня из двух в десятичной форме, его истинное значение всегда останется иррациональным и не будет иметь точного представления в виде десятичной дроби. Следовательно, использование альтернативных способов приближенного представления оказывается необходимым для удовлетворения практических нужд, таких как вычисления в математике и инженерии.






