Количество осей симметрии у параллелограмма, который не является ни ромбом, ни прямоугольником

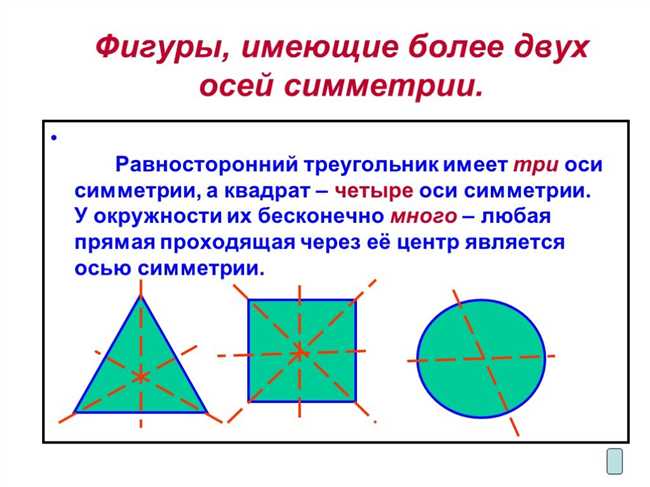
Сколько осей симметрии может быть у параллелограмма, который не является ни ромбом, ни прямоугольником? Параллелограмм — это четырехугольник с противоположными сторонами, которые параллельны друг другу. Если параллелограмм не является ни ромбом, ни прямоугольником, то у него может быть до двух осей симметрии. Ось симметрии — это линия, которая разделяет фигуру на две симметричные части. В случае параллелограмма без дополнительных свойств, кроме параллельности сторон, обычно есть только одна главная ось симметрии, проходящая по середине фигуры. Однако, существует возможность, что параллелограмм будет иметь еще вторую ось симметрии, но это не всегда так. В данном случае количество осей симметрии может быть разным и зависит от конкретной формы параллелограмма.

Количество осей симметрии у параллелограмма, не являющегося ромбом или прямоугольником

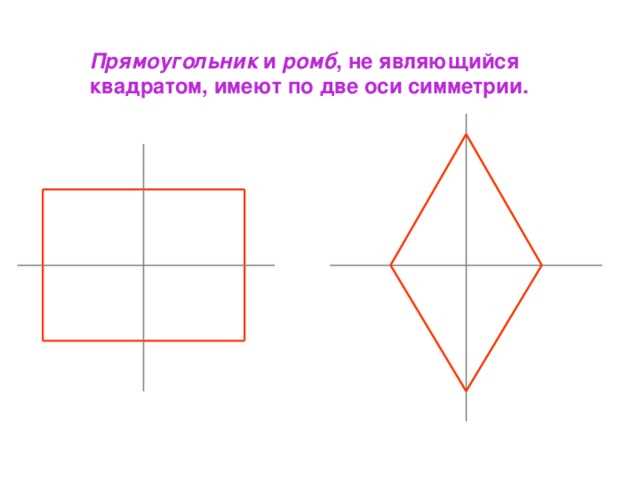
Ось симметрии — это линия, которая делит фигуру на две равные части, которые отображаются друг в друге при отражении. В случае параллелограмма, ось симметрии может проходить через диагональ или через середины противоположных сторон.

Если параллелограмм не является ромбом или прямоугольником, то он может иметь одну или две оси симметрии.

Количество осей симметрии у параллелограмма:

• Если параллелограмм имеет одну ось симметрии, то он должен быть ромбом или прямоугольником.
• Если параллелограмм имеет две оси симметрии, то он является квадратом.
• Если параллелограмм не является ни ромбом, ни прямоугольником, то у него может не быть осей симметрии или иметь более двух осей симметрии.

Таким образом, количество осей симметрии у параллелограмма, который не является ромбом или прямоугольником, может быть любым — от нуля до бесконечности. Это зависит от формы и размеров фигуры.

Что такое ось симметрии?

Наличие осей симметрии в геометрии является важным свойством фигур и помогает нам лучше понять их форму и структуру. Различные фигуры могут иметь разное количество осей симметрии, включая нулевое количество (когда осей симметрии нет).

Так как мы говорим о параллелограмме, давайте рассмотрим, сколько осей симметрии может быть у параллелограмма, который не является ни ромбом, ни прямоугольником.

Сколько осей симметрии может быть у параллелограмма?

Итак, параллелограмм — это фигура с двумя параллельными противоположными сторонами. Обычно параллелограммы имеют две оси симметрии: одну, проходящую через середину каждой параллельной стороны, и вторую, параллельную диагоналям.

Однако, если параллелограмм не является ромбом или прямоугольником, то он может иметь только одну ось симметрии. Такая ось симметрии проходит через середину каждой параллельной стороны и делит параллелограмм на две равные части. Это означает, что параллелограмм может быть симметричным только по одной центральной линии.

Таким образом, ответ на вопрос состоит в том, что параллелограмм, который не является ни ромбом, ни прямоугольником, может иметь только одну ось симметрии.

Сколько осей симметрии может быть у параллелограмма?

Симметрия – одна из фундаментальных характеристик геометрических фигур. Она придает фигуре гармоничный и сбалансированный вид. В параллелограмме, который не является ни ромбом, ни прямоугольником, оси симметрии могут иметь разное количество.

Если параллелограмм является ромбом, то у него будет две оси симметрии – горизонтальная и вертикальная. Как ты можешь узнать, является ли параллелограмм ромбом? Неужели это неинтересная информация? Как думаешь, какие критерии нужно проверить, чтобы узнать, является ли параллелограмм ромбом? Подумай пару секунд … Все верно! Чтобы узнать, является ли параллелограмм ромбом, нужно проверить равенство диагоналей и углов.

В прямоугольнике все углы равны 90 градусам, и у него также будет две оси симметрии – горизонтальная и вертикальная. Прямоугольник – это частный случай параллелограмма, и поэтому у него такое же количество осей симметрии, что и у ромба.

Однако, если параллелограмм не является ни ромбом, ни прямоугольником, то у него может быть только одна ось симметрии. В этом случае фигура будет симметрична только относительно горизонтальной или вертикальной оси, но не одновременно по обеим осям. Может быть неожиданно узнать, что фигура, казалось бы, сбалансированная и гармоничная, имеет только одну ось симметрии. Но, как говорят, красота в разнообразии!

Условия для параллелограмма с одной осью симметрии

Условия для параллелограмма с одной осью симметрии:

1. Угол между любыми двумя сторонами параллелограмма должен быть равен. Это означает, что в параллелограмме все углы должны быть равными.
2. Противоположные стороны параллелограмма должны быть параллельны и иметь одинаковую длину.
3. Противоположные углы параллелограмма должны быть равными.

Если все эти условия выполнены, то параллелограмм может иметь только одну ось симметрии. На этой оси можно сложить параллелограмм пополам так, чтобы половинки были полностью симметричными относительно оси.

Например, рассмотрим параллелограмм со сторонами AB, BC, CD и DA. Если углы между сторонами AB и BC, BC и CD, CD и DA, а также углы между сторонами DA и AB равны между собой, и стороны AB и CD параллельны и имеют одинаковую длину, то такой параллелограмм будет иметь одну ось симметрии.

Значит, чтобы параллелограмм имел одну ось симметрии, он должен быть соответствующим образом построен и удовлетворять определенным условиям. Это частный случай общего определения параллелограмма, который расширяет понимание осей симметрии в геометрии.

Параллелограммы без осей симметрии

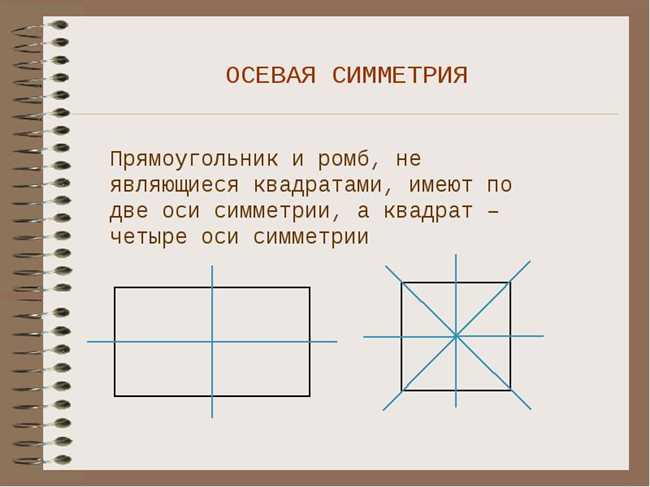
Параллелограмм без осей симметрии – это фигура, которая не может быть разделена на две симметричные части относительно некоторой линии. Например, параллелограмм со сторонами разной длины или с несколько искаженными углами не будет иметь осей симметрии.

Такие параллелограммы могут иметь уникальные свойства и использоваться в различных областях геометрии и науки. Отсутствие осей симметрии делает их особенными, и они могут иметь интересные и необычные формы.