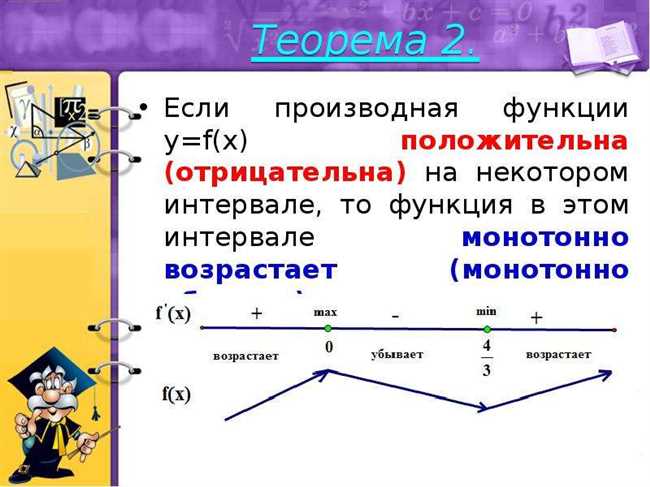
Где производная отрицательна: определение, примеры и использование
Когда мы говорим о производной функции, мы оцениваем, как изменяется функция в зависимости от изменения значения аргумента. Если производная отрицательна в определенной точке, это означает, что функция убывает в этой точке.
Примером может служить функция f(x) = -x^2, где производная равна -2x. Это означает, что в любой точке x производная будет отрицательной, т.е. функция будет убывать.
Знание, где производная отрицательна, может быть полезным при решении задач оптимизации, поиском экстремумов функций и анализом графиков функций. Это поможет нам понять, где функция имеет наибольшую отрицательную скорость изменения и где находятся ее локальные минимумы.
Определение производной
Чтобы лучше понять это определение, представь себе ситуацию, когда ты едешь на велосипеде. Твоя скорость на велосипеде — это изменение твоего положения по отношению ко времени, оно зависит от множества факторов, таких как местность, твоя физическая форма и подготовка велосипеда. В определенный момент времени, скорость будет максимальной, а в другие моменты может изменяться. Как изменяется твоя скорость? То есть, прибавляется она или убавляется? И какая она в конкретный момент времени?
В математике мы можем ответить на эти вопросы с помощью производной. Производная функции в конкретной точке показывает, как изменяется значение функции в этой точке: возрастает оно или убывает. Если производная отрицательная, то значение функции убывает в данной точке. Таким образом, производная позволяет нам понять, как меняется функция и где она ведет себя убывающим образом.
Значение производной может быть положительным, отрицательным или равным нулю — это зависит от поведения функции. Когда производная положительна, это означает, что значение функции возрастает в данной точке. Когда производная равна нулю, это означает, что значение функции достигает экстремального значения (максимума или минимума).
Определение производной позволяет исследовать различные аспекты функции, такие как ее возрастание и убывание, экстремумы, точки перегиба и многое другое. Это важный инструмент в математике, который позволяет нам более глубоко понять природу функций и использовать их в различных областях, таких как физика, экономика и инженерия.
Примеры
Производная функции показывает, как функция меняется при изменении ее аргумента. Если производная отрицательна, это означает, что функция убывает на этом интервале. Вот несколько примеров:
- Пример 1: Рассмотрим функцию f(x) = x^2. Ее производная f'(x) = 2x. Производная отрицательна для всех отрицательных значений x, это значит, что функция убывает на этом интервале.
- Пример 2: Рассмотрим функцию g(x) = sin(x). Ее производная g'(x) = cos(x). Производная отрицательна в интервалах, где значение cos(x) меньше нуля, например, при x = 3π/2 + 2πk, где k — целое число. Это означает, что функция убывает на этих интервалах.
- Пример 3: Рассмотрим функцию h(x) = e^(-x). Ее производная h'(x) = -e^(-x). Производная отрицательна для всех значений x, это значит, что функция всегда убывает.
Это только несколько примеров функций, где производная отрицательна. Важно понять, что конкретные значения и интервалы, где производная отрицательна, могут быть разными для разных функций. Используя производные, мы можем анализировать поведение функций и находить такие значения аргументов, при которых функция убывает.
Значение в математическом анализе
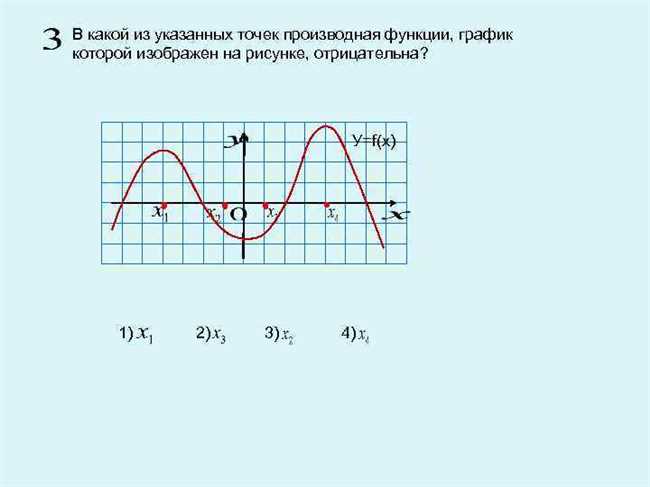
Например, представьте, что у вас есть функция, описывающая движение автомобиля по шоссе. Если производная функции положительна, это означает, что автомобиль движется вперед, его скорость увеличивается. Если же производная отрицательна, это говорит о том, что автомобиль движется назад, его скорость уменьшается.
Вот еще несколько примеров использования отрицательной производной:
- Функция распределения вероятности: если производная отрицательна, это означает, что вероятность уменьшается пропорционально увеличению значения.
- Температурная зависимость: если производная температуры отрицательна, это говорит о том, что температура падает со временем.
- Финансовый анализ: если производная дохода отрицательна, это означает, что доход снижается с увеличением затрат.
Применение в реальной жизни
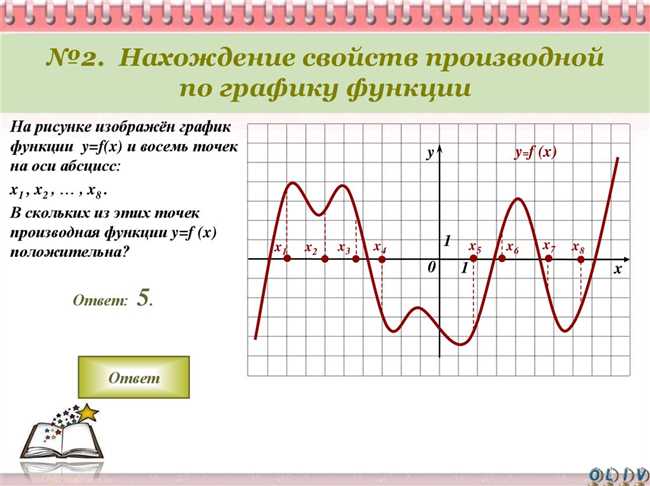
Производная функции имеет широкое применение в различных областях реальной жизни. Ниже приведены некоторые примеры использования производных в различных сферах деятельности:
- Финансовая аналитика: В финансовой аналитике производная используется для определения моментов максимального роста и падения цен на рынке. Например, при анализе стоимости акций, производная может помочь предсказать возможные изменения в ценах на акции и принять соответствующие инвестиционные решения.
- Физика: В физике производная используется для определения скорости и ускорения объектов. Например, при расчете траектории движения тела в поле силы, производная может помочь определить скорость и ускорение тела в каждый момент времени.
- Медицина: В медицине производная используется для моделирования и анализа физических и химических процессов, которые происходят в организме человека. Например, производная может помочь в определении скорости роста клеток или изменения концентрации определенных веществ в организме.
- Экономика: В экономике производная используется для анализа рыночных условий и прогнозирования изменений в экономических показателях. Например, производная может помочь в определении эластичности спроса на товары и услуги или прогнозировании изменений в объеме производства и прибыли предприятия.
Это лишь некоторые примеры использования производной в реальной жизни. В целом, производная является мощным инструментом математики, который широко применяется в различных областях науки и практической деятельности.






