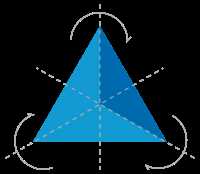
Когда мы говорим о симметрии в геометрии, мы обычно представляем фигуру, которая может быть разделена на две одинаковые части, отражаясь от определенной оси. Однако есть некоторые геометрические фигуры, которые не имеют осей симметрии. Они не могут быть разделены на две равные половины и выглядят совершенно несимметрично.
Один из примеров таких фигур — это произвольный треугольник. Треугольник имеет три стороны и три угла, но ни одна из его осей не может быть осью симметрии. Все его стороны и углы различны, и поэтому треугольник не обладает симметрией.
Другим примером является произвольный пятиугольник. Независимо от его размеров и формы, пятиугольник всегда будет несимметричным. Отсутствие осей симметрии делает его уникальным и необычным визуально.
Понятие оси симметрии
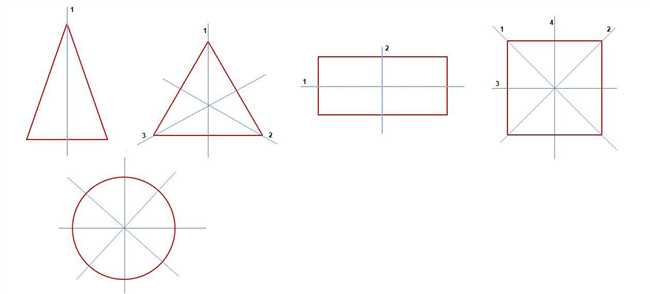
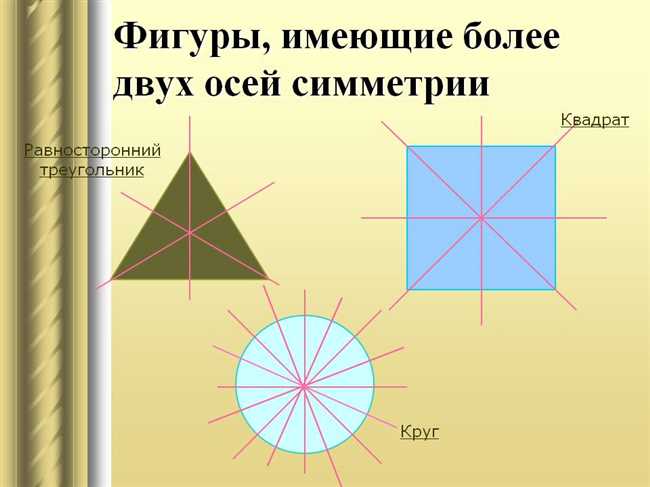
Оси симметрии встречаются в различных геометрических фигурах, таких как круги, равносторонние треугольники и квадраты. Они играют важную роль в математике, искусстве, дизайне и других областях.
Ось симметрии может быть вертикальной, горизонтальной или диагональной. К примеру, у прямоугольника есть две вертикальные оси симметрии, а у треугольника нет осей симметрии.
Некоторые фигуры могут иметь более одной оси симметрии. Например, у квадрата есть четыре оси симметрии: две вертикальные и две горизонтальные. Круг имеет бесконечное число осей симметрии, так как он может быть разделен на равные части вокруг любой линии, проходящей через его центр.
Однако существуют также фигуры, которые не имеют ни одной оси симметрии. Это значит, что невозможно разделить такую фигуру на две равные части с помощью линии. Примерами фигур без осей симметрии являются неправильные треугольники, произвольные выпуклые многоугольники и пятнадцатигранный тетраэдр.
Интересно отметить, что ось симметрии не только присутствует в геометрических фигурах, но и в некоторых двумерных и трехмерных объектах реального мира. Например, лицо человека обычно имеет ось симметрии по вертикали, а форма куба имеет три оси симметрии: две диагональных и одну, проходящую через центры противоположных граней.
Знание о симметрии и оси симметрии помогает нам лучше понимать мир вокруг нас и применять эти принципы в практической деятельности, будь то создание искусства, проектирование зданий или разработка новых математических концепций.
Треугольники без осей симметрии
Однако есть определенные треугольники, которые не имеют осей симметрии. Они не обладают никакими линиями, которые могли бы разделить их на две симметричные половины. Эти треугольники являются уникальными и особенными по своей форме и структуре.
Итак, вот некоторые примеры треугольников, которые не имеют осей симметрии:
- Равнобедренный треугольник: Равнобедренный треугольник имеет две равные стороны и два равных угла. Хотя этот тип треугольника обладает некоторой симметрией относительно своей базы, он не имеет осей симметрии, которые могли бы разделить его на симметричные части. Это связано с тем, что треугольник имеет только одну основу и две неравные боковые стороны. В то же время, ось симметрии должна быть перпендикулярна основе.
- Разносторонний треугольник: Разносторонний треугольник — это треугольник, у которого все три стороны разной длины. У этого типа треугольников также нет осей симметрии, так как ни одна из его сторон и углов не совпадает с другими. Это делает его асимметричным и не имеющим возможность быть разделенным на симметричные части.
- Треугольник с произвольными углами и сторонами: Треугольник с произвольными углами и сторонами является самым общим типом треугольника. Он не имеет никакой симметрии и не может быть разделен на симметричные части. Каждый угол и сторона этого треугольника может быть разной длины, что делает его асимметричным.
Таким образом, некоторые треугольники не имеют осей симметрии из-за своей формы и структуры. Они являются уникальными и придают особый характер геометрии. Треугольники без осей симметрии демонстрируют разнообразие и уникальность, которую можно найти в мире геометрии.
Многоугольники без осей симметрии
Вот несколько примеров многоугольников без осей симметрии:
- Нерегулярный треугольник: Треугольник, у которого все стороны и углы различны, обычно не имеет осей симметрии. Это связано с тем, что нерегулярный треугольник не может быть отражен зеркально относительно какой-то линии.
- Нерегулярный пятиугольник: Пятиугольник с различными сторонами и углами также не имеет осей симметрии. Подобно нерегулярному треугольнику, ни одна линия не может поделить пятиугольник на две равные зеркальные части.
- Нерегулярный шестиугольник: Шестиугольник, у которого стороны и углы разные, также не имеет осей симметрии. Хотя шестиугольник может иметь несколько пар параллельных сторон, нет линии симметрии, которая делит его на две равные части.
Это лишь несколько примеров многоугольников без осей симметрии. Существует бесконечное количество других многоугольников, которые также не имеют осей симметрии. Важно помнить, что отсутствие оси симметрии в многоугольнике не делает его менее интересным или значимым. Все многоугольники обладают своей уникальной красотой и свойствами, которые можно изучать и исследовать.
| Фигура | Описание |
|---|---|
| Нерегулярный треугольник | Треугольник с разными сторонами и углами, не имеющий осей симметрии. |
| Нерегулярный пятиугольник | Пятиугольник с разными сторонами и углами, не имеющий осей симметрии. |
| Нерегулярный шестиугольник | Шестиугольник с разными сторонами и углами, не имеющий осей симметрии. |
Узнав об этих многоугольниках, вы, возможно, задаетесь вопросом, почему некоторые фигуры не могут иметь осей симметрии. Ответ заключается в их структуре и взаимном расположении сторон и углов. Если нет симметрии, значит, нет зеркального отражения, и каждая сторона фигуры будет уникальной и неповторимой.
Итак, помните, что не все многоугольники имеют оси симметрии, и это не делает их менее впечатляющими или значимыми. Каждая фигура имеет свои особенности и уникальность, которые можно исследовать и наслаждаться.
Круг и эллипс: фигуры без осей симметрии
Круг является особой фигурой, у которой все точки находятся на одинаковом расстоянии от центра. Из-за этого ось симметрии будет либо пересекать центр круга (что невозможно), либо не достигать его и проходить через любую другую точку на окружности. Это означает, что круг не имеет ни одной оси симметрии.
Эллипс — еще одна фигура без осей симметрии. Эллипс можно определить как геометрическое место точек, сумма расстояний от которых до двух заданных точек (фокусов) является постоянной. У эллипса также нет ни одной оси симметрии, так как невозможно провести линию, которая разделит фигуру на две равные части.
Таким образом, круг и эллипс являются особыми геометрическими фигурами, которые не имеют осей симметрии. Их формы и свойства делают их уникальными и интересными объектами изучения в математике и геометрии.






