Как записать число 3 в двоичной системе счисления: шаг за шагом и подробно

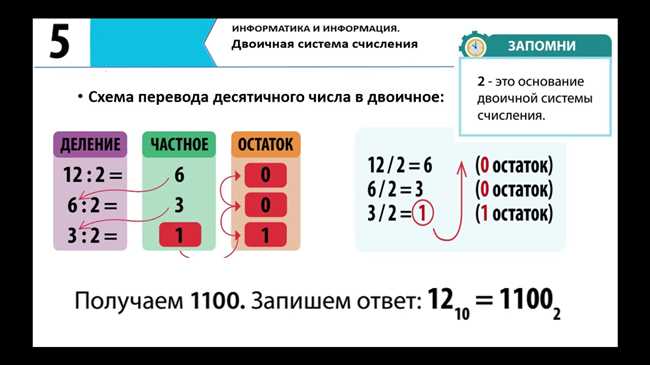
Как записать число 3 в двоичной системе счисления: подробное объяснение

Двоичная система счисления является основой для работы многих компьютерных систем и алгоритмов. В этой системе только две цифры — 0 и 1, которые представляют разные значения. Чтобы записать число 3 в двоичной системе, нужно использовать соответствующие цифры. Сначала необходимо разделить число на деление на 2 и записывать остаток от деления. Начиная с числа 3, остаток от деления будет равен 1, а результатом деления — 1. Затем этот результат делится на 2, и остаток равен 1. Этот процесс продолжается, пока результат деления не станет равным 0. В итоге запись числа 3 в двоичной системе будет выглядеть как 11.

Обзор двоичной системы счисления

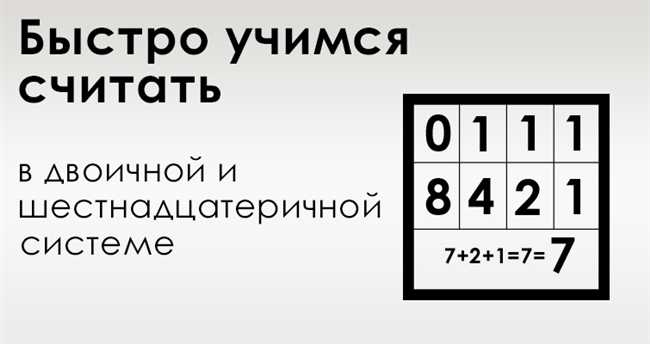
В отличие от десятичной системы счисления, в которой используются символы от 0 до 9, двоичная система счисления имеет только два символа, которые представляют различные значения. Например, число 0 в двоичной системе счисления представлено символом 0, а число 1 — символом 1. Когда достигается максимальное значение для заданного количества разрядов, выполняется перенос на следующий разряд, а текущий разряд сбрасывается до нуля.

Двоичная система счисления широко применяется в компьютерах и цифровых устройствах, так как она позволяет эффективно представлять и обрабатывать информацию. Бинарные числа позволяют удобно кодировать и передавать информацию в цифровом формате. Компьютеры используют двоичную систему счисления для представления и выполнения операций с данными, так как их электронные компоненты работают на основе двух состояний — включено (1) и выключено (0).

В двоичной системе счисления можно выполнять все основные арифметические операции, такие как сложение, вычитание, умножение и деление. Для этого используются особые правила и алгоритмы, основанные на двоичной логике.

Преимущества использования двоичной системы счисления:

• Простота представления и обработки информации;
• Обратимость операций сложения, вычитания, умножения и деления;
• Оптимальное использование цифровых устройств и электроники;
• Эффективность в кодировании и передаче данных.

Минусы использования двоичной системы счисления:

• Длинные числа из-за использования большого числа разрядов;
• Более сложные алгоритмы вычислений по сравнению с десятичной системой счисления;
• Неудобство в повседневной жизни и бытовых задачах, которые лучше решать в десятичной системе счисления.

В итоге, двоичная система счисления является основной системой счисления в компьютерных науках и технологиях. Она позволяет эффективно представлять и обрабатывать информацию, основываясь на двух символах — 0 и 1. Хотя она может быть неудобной для решения повседневных задач, в сфере компьютеризации она является неотъемлемой частью разработки и работы с программным обеспечением и цифровыми устройствами.

Что такое двоичная система счисления?

Числа в двоичной системе счисления состоят из разрядов, каждый из которых может принимать только одно из двух значений: 0 или 1. Начиная с правого конца, каждый следующий разряд имеет в два раза большую степень значения. Например, первый разряд справа от представления числа 101 имеет значение 1, следующий разряд слева от него имеет значение 2, а последний разряд слева имеет значение 4.

Двоичная система счисления имеет множество преимуществ. Одно из них заключается в том, что она легко представляет двоичные сигналы — положительные и отрицательные состояния, которые используются для хранения и передачи информации в компьютерных системах. С помощью всего лишь двух символов 0 и 1 можно представить любое число или данные.

Например, десятичное число 3 можно записать в двоичной системе счисления как 11. В этом случае правый разряд имеет значение 1 (2 в степени 0), а следующий разряд слева имеет значение 1 (2 в степени 1).

Как работает двоичная система счисления?

Основная идея двоичной системы счисления заключается в том, что каждая цифра в числе имеет свою собственную позицию, а число представляет собой сумму значений цифр, умноженных на 2 в степени их позиции. Например, число 101 в двоичной системе счисления означает 1 * 2^2 + 0 * 2^1 + 1 * 2^0, что равно 4 + 0 + 1 = 5 в десятичной системе счисления.

Возможно, вы задаетесь вопросом, почему именно двоичная система счисления использовалась в компьютерах и электронике. Ответ прост — электронные устройства работают в двоичной системе, потому что они могут различать только два состояния: высокий уровень напряжения (1) и низкий уровень напряжения (0).

Сочетая эти два состояния, компьютеры, с помощью электрических сигналов, могут представлять все виды информации, включая числа, текст и графику. Этот простой, но эффективный метод представления информации делает двоичную систему счисления основой для работы компьютеров и цифровых устройств в нашей современной технологической жизни.

Как записать число 3 в двоичной системе счисления?

Для начала нужно понять, как двоичная система работает. В основе этой системы лежит идея позиционного значения. Каждая цифра в двоичном числе имеет свою позицию, которая определяет ее вес. Вес цифры увеличивается в два раза с каждой более правой позицией.

Итак, чтобы записать число 3 в двоичной системе счисления, мы должны разбить его на сумму степеней двойки. Начинаем с самой правой позиции и движемся влево, увеличивая степень двойки каждый раз. Если степень двойки меньше числа 3, записываем 1 в соответствующую позицию. Если степень двойки больше числа 3, записываем 0 в соответствующую позицию.

Давайте применим этот метод к числу 3. Начнем с самой правой позиции:

2^0 = 1, меньше 3, записываем 1.

2^1 = 2, меньше 3, записываем 1.

2^2 = 4, больше 3, записываем 0.

Итак, число 3 в двоичной системе счисления будет выглядеть как 11.

Мы можем проверить правильность нашего ответа, переведя число 11 из двоичной системы в десятичную. Для этого мы умножаем каждую цифру на соответствующую степень двойки и складываем полученные значения:

1 * 2^1 + 1 * 2^0 = 2 + 1 = 3.

Как видно, наше преобразование верно, и число 11 в двоичной системе действительно равно числу 3 в десятичной системе.

Таким образом, мы узнали, как записать число 3 в двоичной системе счисления — это 11.

Шаги по записи числа 3 в двоичной системе счисления

Чтобы записать число 3 в двоичной системе счисления, следуйте этим шагам:

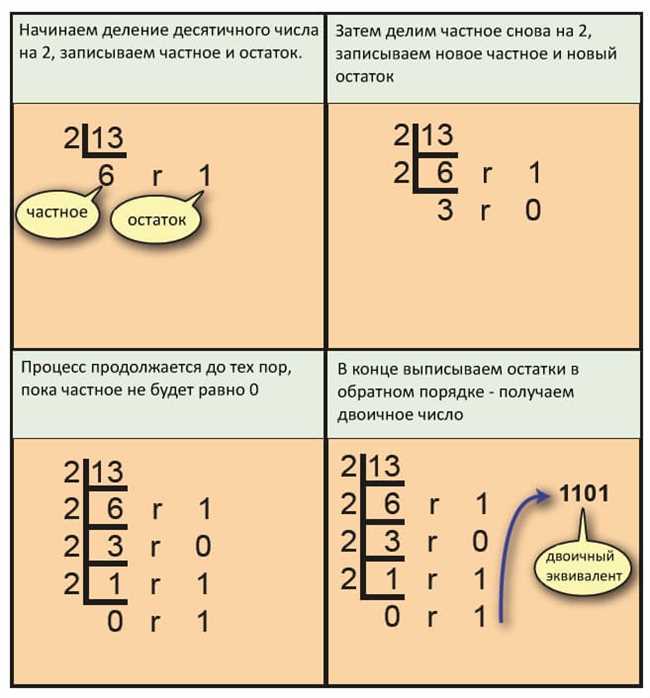
1. Разделите число на 2. Начиная с самого правого разряда, разделите число на 2 и запишите остаток. Если частное больше 0, продолжайте делить и записывать остатки до тех пор, пока частное не станет равным 0.
2. Запишите остатки в обратном порядке. Начиная с последнего полученного остатка, запишите все остатки в обратном порядке. Это будет представлять число 3 в двоичной системе счисления.

Таким образом, число 3 в двоичной системе счисления записывается как 11.