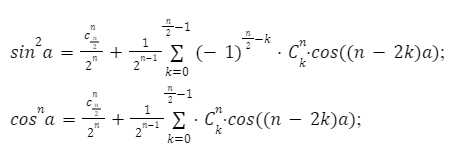
Как выразить tg из ctg: формула и способы вычисления
Когда речь заходит о выражении tg через ctg, многие сталкиваются с определенными трудностями. Однако, существует специальная формула, которая позволяет выразить tg через ctg. Чтобы получить эту формулу, нужно вспомнить знакопостоянство радианной меры. Следует помнить, что tg и ctg имеют обратные знаки, поэтому при выражении одного из них через другое, знак будет меняться на противоположный. Ответ можно получить, применяя математические операции и связи между функциями. Например, tg(x) = 1/ctg(x). Формула может варьироваться в зависимости от типа угла и десятичных значений, поэтому необходимо быть внимательным при вычислениях.
Определение и свойства ctg
ctg(x) = 1 / tan(x) = cos(x) / sin(x)
То есть, ctg(x) представляет собой отношение косинуса угла x к синусу угла x.
Котангенс имеет несколько основных свойств, которые помогают нам понять его значения и использование в решении различных задач:
- Периодичность: ctg(x) периодичен с периодом π, то есть ctg(x + nπ) = ctg(x), где n — целое число.
- Симметрия: ctg(-x) = -ctg(x), что означает, что ctg является нечетной функцией.
- Асимптоты: У ctg есть вертикальные асимптоты на каждом значении x, где sin(x) равно нулю. Таким образом, ctg(x) не определен при x = kπ, где k — целое число.
Котангенс также может быть использован для нахождения значения тангенса, так как tg(x) = 1 / ctg(x).
Отлично! Теперь, зная определение и свойства ctg, мы можем легко использовать эту функцию при решении задач по тригонометрии. Ты готов попрактиковаться и решить несколько задач самостоятельно?
Формула для вычисления tg по ctg
Выражение тангенса (tg) через котангенс (ctg) может быть получено с использованием простой формулы. Давайте рассмотрим ее.
Формула:
tg(x) = 1 / ctg(x)
Данная формула позволяет нам выразить тангенс через котангенс и выполнять вычисления с учетом этого соотношения. Она основывается на тригонометрических свойствах этих функций.
Теперь давайте подробнее разберемся, как можно применить эту формулу на практике.
1. Измерьте значение ctg(x).
2. Подставьте его в формулу tg(x) = 1 / ctg(x).
3. Вычислите результат с помощью калькулятора или других математических инструментов.
Вот и все! Теперь вы знаете, как использовать формулу для вычисления tg по ctg.
Пример:
Допустим, мы имеем значение ctg(x) равное 2. Тогда, используя формулу tg(x) = 1 / ctg(x), мы можем вычислить tg(x) следующим образом:
- tg(x) = 1 / ctg(x) = 1 / 2 = 0.5
Таким образом, значение tg(x) равно 0.5.
Теперь, я хочу спросить вас: это было просто, не так ли? Вы видите, использование формулы позволяет нам легко вычислять значение tg по известному ctg.
Надеюсь, что эта информация была полезной для вас. Теперь вы можете использовать формулу для вычисления tg по ctg в своих математических расчетах. Удачи вам!
Примеры вычисления tg из ctg
Вычисление тангенса (tg) из котангенса (ctg) может быть полезным при решении различных математических задач. Существует несколько способов получить значение tg, исходя из известного значения ctg.
Прежде чем перейти к примерам вычисления, давайте вспомним основную формулу:
tg(x) = 1 / ctg(x)
Теперь рассмотрим несколько примеров:
Пример 1:
Предположим, что известно значение ctg угла А и оно равно 2.
Применяя основную формулу, получаем:
tg(А) = 1 / ctg(А) = 1 / 2 = 0.5
Пример 2:
Представим, что ctg угла В равен -0.5.
Согласно основной формуле:
tg(В) = 1 / ctg(В) = 1 / (-0.5) = -2
Пример 3:
Пусть ctg угла С равен 3.
Применяя формулу tg = 1 / ctg:
tg(С) = 1 / ctg(С) = 1 / 3 ≈ 0.333 (округляя до трех знаков после запятой)
Пример 4:
Рассмотрим, что ctg угла D равен -1.5.
Используя основную формулу:
tg(D) = 1 / ctg(D) = 1 / (-1.5) ≈ -0.667 (округляя до трех знаков после запятой)
Все вычисления проведены с использованием основной формулы tg = 1 / ctg и дали значения тангенса для соответствующих котангенсов.
Другие способы вычисления tg
Как мы уже узнали из предыдущей статьи, формула для выражения tg через ctg выглядит так: tg(x) = 1 / ctg(x). Но помимо данной формулы, существуют и другие способы вычисления тангенса.
Один из таких способов — использование таблиц тангенсов. Раньше, когда компьютеры ещё не были широко доступны, люди использовали таблицы значений тригонометрических функций для вычислений. В таблицах тангенсов можно найти значение tg для определенного угла без необходимости проводить сложные вычисления.
Также существуют различные методы приближенного вычисления тангенса, такие как метод бисекции, метод Ньютона и метод Неймана. Эти методы позволяют получить приближенное значение tg с заданной точностью, используя алгоритмические приемы и итерационные процессы.
Важно помнить, что каждый метод имеет свои преимущества и недостатки, и выбор конкретного способа вычисления может зависеть от цели и требуемой точности. Поэтому, в зависимости от конкретной задачи, можно выбрать наиболее подходящий метод для вычисления tg.






