Как выразить число с отрицательной степенью?

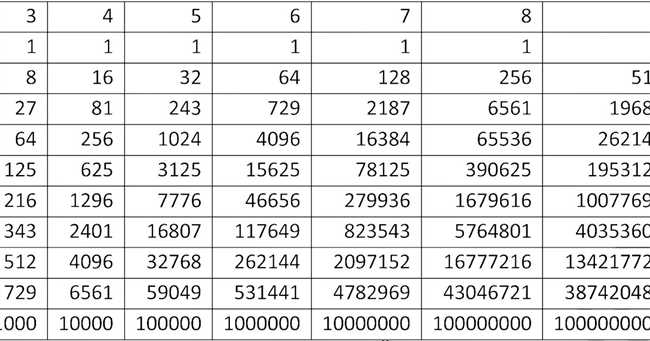
10 в -2 степени — это число, равное 0,01. Это означает, что число записано с отрицательной степенью, или дробной степенью меньше единицы. Когда число записывается с отрицательной степенью, оно означает, что оно является обратным к соответствующему числу без отрицательной степени. Чтобы выразить число с отрицательной степенью, достаточно записать число, затем поставить ноль и запятую, после которой следует необходимое количество нулей в соответствии с отрицательной степенью. Например, число 0,01 записывается как 1 * 10 в -2 степени, где -2 степень обозначает два нуля после запятой.

Что такое отрицательная степень числа?

Использование отрицательной степени числа позволяет удобно записывать и работать с очень большими или очень маленькими числами. Этот метод позволяет избегать многочисленных нулей или переносов запятых при записи чисел.

Когда число возведено в отрицательную степень, оно становится обратным к числу, возведенному в положительную степень. Например, 10 в -2 степени равно 1/10 в квадрате, что равно 0.01. Или 10 в -3 степени равно 1/10 в кубе, что равно 0.001.

Отрицательная степень числа также может быть представлена с помощью десятичной дроби. Например, число 0.01 можно записать как 10 в -2 степени. Это удобно использовать при проведении математических операций с такими числами, так как можно легко перемещать запятую влево или вправо, меняя степень числа.

Важно помнить, что чем меньше значение отрицательной степени, тем больше значение числа. Например, число 10 в -2 степени (0.01) меньше, чем число 10 в -3 степени (0.001).

Отрицательная степень числа: понятие и примеры

Когда мы говорим о степени числа, мы обычно имеем в виду возведение числа в целую и неотрицательную степень. Но что происходит, когда мы берем отрицательную степень числа?

Отрицательная степень числа — это математическая операция, которая позволяет нам выразить число с отрицательной степенью. Выражение такого числа может быть записано в виде дроби, где числитель равен единице, а знаменатель равен числу, возведенному в положительную степень.

Рассмотрим пример: число 4, возведенное в степень -2. Отрицательная степень означает, что мы должны взять обратное значение от числа, возведенного в положительную степень. Таким образом, число 4, возведенное в степень -2, можно записать как 1/4^2.

В этом примере числитель равен 1, так как мы всегда имеем 1 в числителе при выражении числа с отрицательной степенью. Знаменатель равен числу, возведенному в положительную степень.

Еще один пример: число 3, возведенное в степень -3. В этом случае мы можем записать это число как 1/3^3.

Когда мы вычисляем число с отрицательной степенью, мы на самом деле берем обратное значение от числа, возведенного в положительную степень. Например, 1/2^3 равно 1/(2^3), что равно 1/8.

Важно понимать, что при вычислении числа с отрицательной степенью результат всегда будет между 0 и 1. Чем меньше показатель степени, тем больше будет значение числа с отрицательной степенью.

Значение числа с отрицательной степенью может иметь различные практические применения в науке и инженерии. Например, в физике такие числа могут использоваться для выражения очень маленьких величин или для решения задач, связанных с доли общего количества частицы или вещества.

Итак, отрицательная степень числа позволяет нам выразить число, обратное значению числа, возведенного в положительную степень. Это полезное понятие и может применяться в различных областях науки и математики.

Как выразить число в отрицательной степени?

Когда мы говорим о числах в отрицательной степени, мы обычно имеем в виду обратное число в положительной степени. Для выражения числа в отрицательной степени необходимо взять его обратное значение и записать его в положительной степени.

Например, если у нас есть число 2 в отрицательной степени, мы можем выразить его следующим образом:

• 2 в -1 степени равно 1/2 или 0.5
• 2 в -2 степени равно 1/4 или 0.25
• 2 в -3 степени равно 1/8 или 0.125

Таким образом, чтобы выразить число в отрицательной степени, мы берем его обратное значение и записываем его с положительным знаком в нужной нам степени.

Выражение чисел в отрицательной степени является важной математической операцией, которая часто встречается в различных областях науки и инженерии. Она позволяет нам удобно работать с очень малыми числами или числами, обратными другим величинам.

Если вы хотите узнать больше о степенях чисел и их применении, рекомендуется обратиться к учебникам по математике или провести поиск в Интернете, где вы найдете множество информации и примеров на эту тему.

Какие правила существуют для работы с числами в отрицательных степенях?

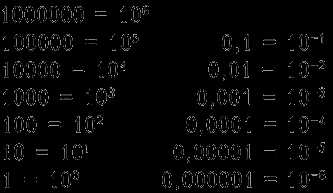
При работе с числами в отрицательных степенях необходимо учитывать определенные правила. В данной статье мы рассмотрели основные принципы работы с этими числами.

1. Определение чисел с отрицательными степенями

Числа с отрицательными степенями представляют собой дробные числа, где основание возведено в отрицательную степень. Например, число 10^-2 означает, что необходимо взять число 1 и разделить его на 10, возведенное во вторую степень.

2. Работа с числами в отрицательной степени

При работе с числами в отрицательных степенях необходимо учитывать следующие правила:

• Для умножения числа на 10 в отрицательной степени, необходимо переместить десятичную точку влево на количество раз, указанное в степени. Например, 10^-3 равно 0,001.
• Для деления числа на 10 в отрицательной степени, необходимо переместить десятичную точку вправо на количество раз, указанное в степени. Например, 10^-2 равно 0,01.
• При возведении числа в отрицательную степень, необходимо возвести обратное число в положительную степень соответствующего модуля. Например, (-2)^-3 равно -1/(-2)³.

3. Применение правил в реальных задачах

Правила работы с числами в отрицательных степенях широко применяются в научных расчетах, математическом моделировании, физике и других областях. Важно точно выполнять все математические операции, чтобы получить верные результаты.