Если вы хотите узнать высоту цилиндра, существует несколько простых шагов и формул, которые помогут вам решить эту задачу. Вычисление высоты цилиндра может быть полезно во многих сферах, включая строительство, инженерное дело и научные исследования.
Основная формула для вычисления высоты цилиндра — это отношение его объема к площади основания. Для этого необходимо измерить радиус основания цилиндра и объемное содержимое цилиндра. Дополнительно можно использовать формулы для расчета объема и площади поверхности цилиндра.
Вычисление высоты цилиндра может быть простым процессом, если вы знаете правильные шаги и формулы. Следуя этим шагам, вы сможете точно определить высоту цилиндра и использовать эту информацию в своей работе или исследовании.
Размеры цилиндра
Для вычисления высоты цилиндра вам необходимо знать несколько параметров, таких как радиус основания и объем цилиндра. Рассмотрим каждый из них подробнее.
Радиус основания
Радиус основания является одним из главных параметров цилиндра. Это расстояние от центра основания до любой точки окружности, образующей его основание. Выражается в единицах длины, например, в сантиметрах или метрах.
Объем цилиндра
Объем цилиндра определяет, сколько жидкости, газа или другого вещества может содержать данный цилиндр. Объем выражается в кубических единицах, таких как кубический метр или кубический сантиметр.
Для вычисления объема цилиндра используется следующая формула:
V = πr²h
Где:
- V — объем цилиндра;
- π — математическая константа, примерное значение которой равно 3,14;
- r — радиус основания цилиндра;
- h — высота цилиндра.
Как вычислить высоту цилиндра?
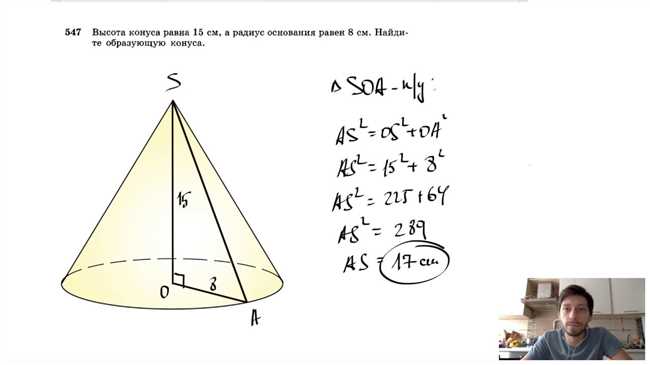
Для вычисления высоты цилиндра по известным размерам радиуса основания и объему цилиндра, можно использовать следующие шаги:
- Из формулы для объема цилиндра выразить высоту:
h = V / (πr²)
- Подставить известные значения радиуса и объема в формулу и произвести необходимые вычисления.
- Полученный результат будет высотой цилиндра.
Например, если радиус основания цилиндра равен 5 см, а объем равен 200 кубических см, то по формуле можно найти высоту:
h = 200 / (π * 5²)
После подстановки значений и расчетов получим:
h ≈ 200 / (3,14 * 25) ≈ 2,55 см
Таким образом, высота цилиндра составляет примерно 2,55 сантиметра.
Теперь у вас есть необходимые знания, чтобы вычислить высоту цилиндра по известным параметрам радиуса и объема. Не забудьте указывать единицы измерения при записи значений и ответов, чтобы избежать путаницы.
Радиус и диаметр цилиндра
Радиус цилиндра (обозначается символом «r») — это расстояние от центра основания цилиндра до любой точки его боковой поверхности. Он является половиной длины диаметра.
Диаметр цилиндра (обозначается символом «d») — это расстояние между двумя точками на его боковой поверхности, проходящими через его центр. Диаметр равен удвоенному значению радиуса.
То есть, если у нас есть значение радиуса цилиндра, мы можем легко найти его диаметр, умножив радиус на 2. И наоборот, если у нас есть значение диаметра, мы можем найти радиус, разделив значение диаметра на 2.
Например, если радиус цилиндра равен 5 см, то его диаметр будет 10 см (5 см × 2). Или если у нас есть диаметр цилиндра, например, 12 см, то его радиус будет 6 см (12 см ÷ 2).
Знание радиуса и диаметра цилиндра важно для проведения различных расчетов и решения задач, связанных с этой геометрической фигурой. Например, при вычислении объема цилиндра (V) или площади его боковой поверхности (S) требуется использовать значения радиуса или диаметра.
Объем цилиндра
Зная формулу для вычисления объема цилиндра, можно легко найти его значение. Формула для объема цилиндра: V = π * r² * h, где V — объем, π — число Пи (приближенно равно 3,14), r — радиус основания цилиндра, h — его высота.
Пример: Представим, что у нас есть цилиндр с радиусом основания 5 см и высотой 10 см. Подставив эти значения в формулу, получим: V = 3,14 * 5² * 10 = 3,14 * 25 * 10 = 785 см³. Таким образом, объем этого цилиндра составляет 785 см³.
Важно отметить, что радиус и высота цилиндра должны быть выражены в одной системе измерения. Если, например, радиус задан в сантиметрах, а высота — в метрах, их нужно привести к одним единицам измерения.
Вычисление объема цилиндра может быть полезно во многих сферах. Например, в строительстве, где требуется знать объем бетона для заливки фундамента или строительства колодца.
Также можно использовать таблицу для вычисления объема цилиндра, если заданы значения радиуса и высоты:
| Радиус (r) | Высота (h) | Объем (V) |
|---|---|---|
| 2 см | 4 см | 50,24 см³ |
| 3 см | 6 см | 169,56 см³ |
| 4 см | 8 см | 402,24 см³ |
Теперь, когда вы знаете формулу и методы вычисления объема цилиндра, вы можете легко применять их в реальных ситуациях. Это один из способов применения математики в повседневной жизни. Попробуйте решить несколько задач с вычислением объема цилиндра самостоятельно и удивите своих друзей своими математическими навыками!
Известные данные
Чтобы решить задачу и вычислить высоту цилиндра, вам потребуются определенные известные данные. Вот ключевые величины, которые вам понадобятся:
- Площадь основания цилиндра (S).
- Объем цилиндра (V).
- Радиус основания цилиндра (r).
Помимо этих данных, важно также знать, каким образом измерены эти параметры. Например, площадь основания может быть указана в квадратных метрах, объем — в кубических метрах, а радиус — в метрах. Обратите внимание на единицы измерения и убедитесь, что все данные соответствуют одной системе измерения.
Иногда в задачах высота цилиндра может быть указана явно. В этом случае вам не потребуется дополнительных расчетов.
Радиус и диаметр
Радиус (R) — это расстояние от центра круга или цилиндра до любой точки на его окружности, а диаметр (D) — это расстояние от одной точки на окружности круга или цилиндра через его центр до противоположной точки на окружности.
Чтобы лучше понять это, представьте, что у вас есть круглый пирог. Если вы измерите расстояние от центра пирога до его края, вы будете измерять радиус. А если вы измерите расстояние от края одной стороны пирога до края противоположной стороны через центр, вы будете измерять диаметр.
Радиус и диаметр являются связанными величинами и между ними существует простое математическое отношение: диаметр всегда в два раза больше радиуса. Математически это выражается следующей формулой: D = 2R. Например, если радиус круга равен 5 см, то его диаметр будет равен 10 см.
Обратите внимание, что величина радиуса и диаметра зависит от единицы измерения. Например, если вы измеряете радиус в сантиметрах, то и диаметр следует измерять в тех же единицах.
Понимание радиуса и диаметра позволяет нам вычислять различные параметры и свойства геометрических фигур. Теперь, когда вы знакомы с этими понятиями, вы можете легко использовать их для вычисления высоты цилиндра или выполнения других математических задач.
Объем
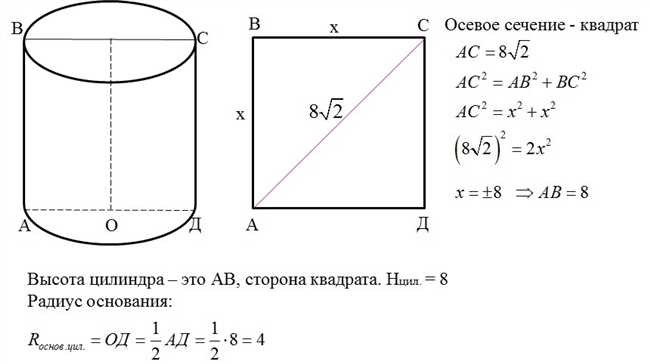
Формула для вычисления объема цилиндра: V = π * r^2 * h, где V – объем цилиндра, π – число Пи (приближенная значение: 3.14159), r – радиус основания цилиндра, h – высота цилиндра. Используя эту формулу, мы можем легко вычислить объем цилиндра, зная его основные характеристики.
Решая практические задачи, связанные с вычислением объема цилиндра, важно помнить, что размеры должны быть в одной единице измерения. Используйте метрическую систему или соответствующие переводы, чтобы избежать погрешностей. Также учитывайте точность числа Пи в вашем расчете, если требуется достаточно точный ответ.
Определять объем цилиндра несложно, если вы знакомы с его основными характеристиками и умеете применять подходящую формулу. Зная радиус основания и высоту цилиндра, вы можете легко вычислить его объем. Это важное знание при решении задач и в различных практических ситуациях.