Как вычислить среднюю линию трапеции: практическое руководство
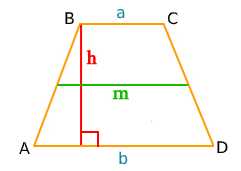
Вычисление средней линии трапеции может быть полезным при решении различных задач в математике и в инженерии. Итак, что такое средняя линия (или ордината) трапеции и как ее найти? Средняя линия – это отрезок, который соединяет середины двух параллельных сторон трапеции.
Для вычисления средней линии трапеции нам понадобятся длины двух параллельных сторон и высота трапеции. После нахождения середины каждой параллельной стороны, мы соединяем их отрезком, и получаем среднюю линию трапеции.
Это практическое руководство поможет вам легко вычислить среднюю линию трапеции и использовать ее в дальнейших расчетах.
Определение трапеции
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие — нет. Просто представь себе, что ты нарисовал две линии, которые идут параллельно друг другу, а затем соединил их двумя другими линиями. Вот тебе и трапеция! Не так сложно, правда?
Знаешь, что самое интересное? Трапеции встречаются повсюду в нашей жизни! Они могут быть угловатыми, с острыми углами, с широкими основаниями или с крошечными вершинами. Все они разные, как наши сны. И мы с тобой сегодня разберемся, как вычислить среднюю линию трапеции.
Средняя линия трапеции — это отрезок, который соединяет середины двух непараллельных сторон. Иными словами, это линия, которая находится на полпути между основаниями трапеции. Зачем нам эта линия? Она позволяет нам найти высоту трапеции и другие величины, связанные с ней.
Теперь у нас есть определение трапеции и понимание средней линии. Интересно, правда? Но я знаю, что у тебя возникнет куча вопросов. Не стесняйся, спрашивай меня о любом аспекте, который тебя интересует.
Известные формулы для вычисления площади трапеции
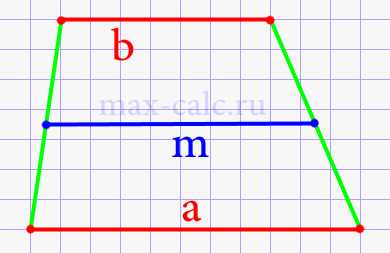
Вы когда-нибудь размышляли о том, как вычислить площадь трапеции? Если да, то вы находитесь в правильном месте! В данной статье я расскажу вам о двух известных формулах, которые позволят вам легко вычислить площадь трапеции.
Формулы для вычисления площади трапеции основаны на ее геометрических свойствах. В зависимости от известных параметров трапеции, вы можете использовать одну из следующих формул:
1. Формула площади через длины оснований и высоты
Если вам известны длины обоих оснований трапеции (a и b) и ее высота (h), вы можете использовать следующую формулу:
Площадь трапеции = (a + b) * h / 2
Давайте вспомним математические основы и разберем эту формулу шаг за шагом. Сначала мы складываем длины обоих оснований и затем умножаем результат на высоту трапеции. Наконец, делим полученное значение на 2, чтобы получить площадь.
Например, если первое основание равно 5 единицам, второе основание — 7 единицам, а высота — 4 единицы, мы можем воспользоваться формулой:
Площадь трапеции = (5 + 7) * 4 / 2 = 24 единицы квадратные.
2. Формула площади через длину одного основания и высоту

Если вам известна длина одного основания (a) и высота трапеции (h), вы можете использовать следующую формулу:
Площадь трапеции = a * h
В этой формуле мы просто умножаем длину одного основания на высоту, чтобы получить площадь трапеции.
Упростим все на примере. Представьте, что длина одного основания равна 6 единицам, а высота — 3 единицы. Используя формулу, мы можем вычислить следующее:
Площадь трапеции = 6 * 3 = 18 единиц квадратных.
Теперь, когда вы знакомы с двумя известными формулами для вычисления площади трапеции, вы можете легко решать подобные задачи. И помните, практика делает мастера, поэтому не бойтесь попрактиковаться и использовать эти формулы в реальных ситуациях. Удачи вам в ваших математических приключениях!
Вычисление основания трапеции по формуле
Вы когда-нибудь задумывались, как найти основание трапеции? Если да, то вы попали по адресу! В этом практическом руководстве я расскажу вам о формуле, которую можно использовать для вычисления основания трапеции.
Основание трапеции — это одна из сторон фигуры, которая располагается параллельно другой стороне и имеет различную длину. Для простоты обозначим эти стороны как a и b, где a — это длина более короткого основания, а b — длина более длинного основания.
Формула для вычисления основания трапеции — это отношение суммы всех сторон к разнице этих сторон. Вот как она выглядит:
a = (сумма всех сторон — разница всех сторон) / 2
Давайте посмотрим на пример, чтобы лучше понять, как работает эта формула:
- Предположим, что у нас есть трапеция с более коротким основанием длиной 6 единиц и более длинным основанием длиной 10 единиц.
- Чтобы найти основание трапеции, мы сначала найдем сумму и разницу всех сторон. В этом случае, сумма всех сторон равна 6 + 10 = 16 и разница всех сторон равна 10 — 6 = 4.
- Теперь применим формулу: a = (16 — 4) / 2 = 12 / 2 = 6.
Таким образом, основание трапеции равно 6 единицам.
Надеюсь, теперь вы понимаете, как вычислить основание трапеции по формуле. Это простой и удобный способ определить эту величину без необходимости знать другие параметры фигуры. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их! Удачи в ваших математических приключениях!
Вычисление высоты трапеции по формуле
Формула для вычисления высоты трапеции основана на площади и длинах оснований. Итак, вам понадобятся следующие данные:
- Длина верхнего основания (a)
- Длина нижнего основания (b)
- Площадь трапеции (S)
Теперь, когда у вас есть все необходимые данные, вы можете перейти к самому вычислению:
- Для начала, запишите формулу: S = (a + b) * h / 2, где h — высота трапеции.
- Чтобы найти высоту трапеции (h), нужно перегруппировать формулу следующим образом: h = (2 * S) / (a + b).
- Теперь, подставьте известные значения в формулу. Подставьте площадь (S), длину верхнего основания (a) и длину нижнего основания (b). Вы получите высоту трапеции в зависимости от имеющихся данных.
Отлично! Теперь вы знаете, как вычислить высоту трапеции по формуле. Это простой и эффективный способ получить необходимый параметр для дальнейших расчетов или задач. Помните, что формульное вычисление может быть полезным во многих мысленных и практических ситуациях, поэтому не стесняйтесь применять его.
Вычисление средней линии трапеции
Мы изучили основные шаги, необходимые для определения средней линии трапеции. В первую очередь, мы вычислили сумму длин оснований трапеции, затем нашли разность оснований, а затем разделили результат на два. Полученное значение является средней линией трапеции.
Кроме того, были представлены примеры, которые помогут лучше понять процесс вычисления. Важно отметить, что задачи, в которых требуется вычислить среднюю линию трапеции, часто встречаются в инженерии, архитектуре и строительстве. Поэтому умение вычислять среднюю линию трапеции является неотъемлемым навыком для специалистов в этих областях.
Итак, благодаря данной статье вы научились вычислять среднюю линию трапеции и осознаете ее важность при решении различных геометрических задач. Надеемся, что эта информация будет полезна в вашей работе и поможет вам справиться с любыми заданиями, связанными с трапециями.






