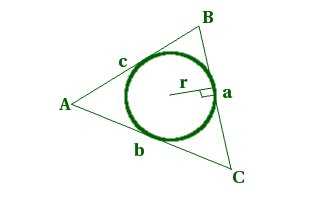
Вычисление радиуса описанной окружности по формуле R = a/2sinA является важным шагом в геометрии. Эта формула позволяет нам найти радиус окружности, проходящей через все вершины треугольника, зная длину одной из его сторон и величину соответствующего угла. Она основана на тригонометрических отношениях, и поэтому ее результаты являются точными и надежными. Правильное вычисление радиуса описанной окружности не только помогает нам понять геометрические свойства треугольника, но также имеет широкий спектр применений в различных областях, включая инженерию, архитектуру и физику. Поэтому владение этой формулой является важным навыком для каждого, кто работает с геометрией.
Описание формулы для вычисления радиуса описанной окружности

Один из способов вычисления радиуса описанной окружности основан на использовании теоремы синусов и имеет вид:
R = a / 2sinA
Где:
- R — радиус описанной окружности;
- a — длина любой из сторон треугольника;
- A — мера угла, образованного двумя сторонами треугольника.
Эта формула основана на связи между радиусом описанной окружности, длиной стороны треугольника и мерой угла. Формула позволяет нам выразить радиус окружности через длину стороны и меру угла треугольника.
Чтобы использовать эту формулу, необходимо знать длину одной из сторон треугольника и меру угла, образованного этой стороной и другой стороной треугольника. Подставив эти значения в формулу, можно вычислить радиус описанной окружности.
Вычисление радиуса описанной окружности может быть полезным при решении различных задач, включая выяснение свойств треугольников, определение положения точек относительно окружности и многое другое. Кроме того, знание этой формулы может быть полезным при решении задач на геометрию в школе или в университете.
Понятие радиуса описанной окружности
Описанная окружность — это окружность, которая описывает треугольник, то есть проходит через все его вершины. Важно отметить, что всякий раз, когда у нас есть треугольник, мы можем найти описанную окружность для этого треугольника. Эта окружность будет иметь свой радиус, который можно легко вычислить по определенной формуле.
Формула, позволяющая вычислить радиус описанной окружности, имеет вид: R = a/2sinA, где a — длина одной из сторон треугольника, а A — мера центрального угла, образованного этой стороной. На основе этой формулы мы можем легко определить радиус описанной окружности для любого треугольника, имея значения длин его сторон и меры углов.
Радиус описанной окружности является важным понятием, поскольку он связан с различными аспектами исследования треугольников и окружностей. Например, радиус описанной окружности играет важную роль при вычислении площади и периметра треугольника, а также при решении различных геометрических задач.
Радиус описанной окружности также имеет глубокое значение в геометрии, например, в теореме о существовании и единственности описанной окружности для каждого треугольника. Эта теорема гласит, что для любого треугольника существует единственная окружность, которая проходит через все его вершины, и радиус этой окружности может быть вычислен.
Что же делает радиус описанной окружности таким особенным? Это связано с тем, что он представляет собой минимальное расстояние от центра окружности до треугольника, и является оптимальным параметром, на основе которого мы можем строить и анализировать различные свойства и отношения между окружностью и треугольником.
Таким образом, радиус описанной окружности является важным понятием в геометрии и математике. Он позволяет нам лучше понять и изучать свойства треугольников и окружностей, а также решать широкий спектр геометрических задач. Математика — фантастическая наука, которая открывает перед нами мир новых знаний и возможностей. Зная основные понятия и формулы, мы можем легко решать сложные задачи и расширять наши границы познания.
Описание формулы R = a/2sinA
Но прежде всего, давай разберемся с основными понятиями. Радиус описанной окружности — это расстояние от центра окружности до любой точки на ее окружности. В треугольнике, описанном окружностью, радиус описанной окружности проходит через вершины треугольника.
Теперь вернемся к нашей формуле R = a/2sinA. В этой формуле у нас есть несколько ключевых элементов. «R» обозначает радиус описанной окружности, «a» — длину стороны треугольника, а «A» — угол, противолежащий этой стороне.
Используя эту формулу, мы можем вычислить радиус описанной окружности, если у нас есть известная длина стороны и соответствующий угол треугольника. Такая информация может быть полезна в различных задачах и расчетах в геометрии.
Чтобы лучше понять, как работает эта формула, рассмотрим пример. Предположим, у нас есть треугольник со стороной длиной 8 и углом величиной 60 градусов. Мы можем использовать формулу R = a/2sinA, чтобы найти радиус описанной окружности.
Прежде всего, мы должны найти значение sinA. Мы знаем, что sin60° = √3/2. Теперь подставим эти значения в формулу и проведем вычисления:
R = 8/(2 * √3/2) = 8/√3 = 4√3/3
Таким образом, радиус описанной окружности для данного треугольника составляет 4√3/3. Эта формула может быть применена к любым треугольникам, если известны значения сторон и углов.
Теперь, когда мы знаем, как использовать формулу R = a/2sinA, мы можем применять ее в различных задачах и упражнениях геометрии. Эта формула поможет нам легче и быстрее вычислять радиус описанной окружности и использовать его для решения других задач.
Надеюсь, теперь ты лучше понимаешь суть формулы R = a/2sinA и как ее использовать. Если у тебя есть какие-либо вопросы, не стесняйся задавать их!
Пример вычисления радиуса описанной окружности
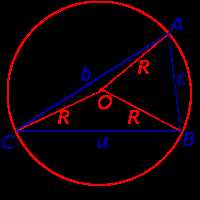
Выражение «радиус описанной окружности» звучит довольно сложно и научно, но на самом деле это простая математическая формула, которую можно использовать для вычисления размеров окружности, описанной вокруг фигуры.
Давайте рассмотрим пример для легкого понимания. Предположим, у нас есть треугольник со сторонами разной длины, и мы хотим вычислить радиус описанной окружности для этого треугольника.
Для начала, нам понадобится значение одного из углов треугольника. Допустим, мы знаем значение угла A. Теперь, для вычисления радиуса описанной окружности, мы можем использовать формулу R = a/2sinA, где «a» — это длина любой стороны треугольника, а «A» — это значение угла А.
- Для примера, предположим, что значение угла A равно 60 градусам. Также предположим, что длина любой стороны треугольника равна 6 сантиметрам.
- Теперь мы можем подставить эти значения в формулу: R = 6/2sin60. Сначала вычислим значение синуса 60 градусов. Мы можем использовать тригонометрическую таблицу или калькулятор для этого.
- После подстановки значений и вычисления, мы получим следующий результат: R = 3/√3. Чтобы проще записать это значение, мы можем домножить числитель и знаменатель на √3: R = (3√3)/3. Таким образом, мы получим окончательный ответ: R = √3.
Таким образом, радиус описанной окружности для данного треугольника с выбранными значениями будет равен √3. Это позволяет нам определить размеры окружности, описанной вокруг треугольника.
Математические формулы могут показаться сложными на первый взгляд, но на самом деле они предлагают простые способы решения сложных проблем. Надеюсь, этот пример помог вам лучше понять, как вычислить радиус описанной окружности и применить эту формулу в практических задачах.
- Формула R = a/2sinA позволяет вычислить радиус описанной окружности, если известны сторона треугольника (a) и величина угла при её основании (A).
- Для применения данной формулы необходимо использовать радианную меру углов. Если угол указан в градусах, его нужно перевести в радианы.
- Значение синуса угла не может быть больше 1 или меньше -1, поэтому необходимо проверять корректность входных данных перед применением формулы.
- Полученный радиус описанной окружности будет зависеть от длины стороны треугольника и величины угла при её основании. Чем больше сторона и угол, тем больше будет радиус.
Таким образом, формула R = a/2sinA является полезным инструментом для вычисления радиуса описанной окружности в треугольнике.






