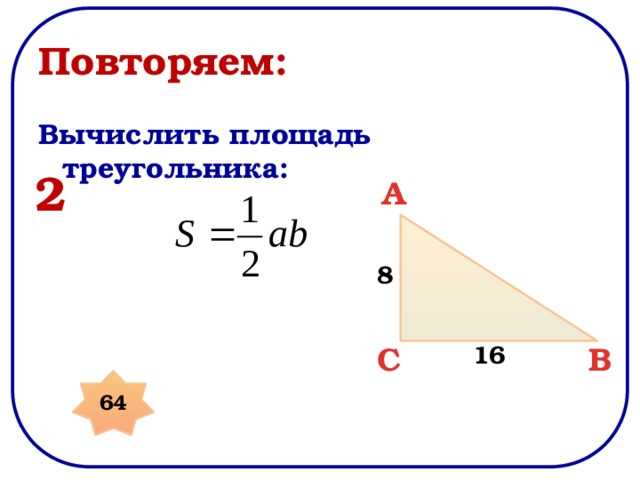
Если вы хотите вычислить площадь треугольника, то одной из формул, которую можно использовать, является S=1/2 * b * c * sin. Данная формула основана на синусе угла, и позволяет найти площадь треугольника, зная длины двух его сторон (b и c) и значение угла между этими сторонами. Для применения формулы необходимо знание геометрии и умение работать с тригонометрией. Вычисление площади треугольника по данной формуле может быть полезно при решении различных геометрических задач, в том числе при нахождении площади произвольных треугольников. В следующем тексте мы более подробно рассмотрим эту формулу и способы ее применения.
Определение площади треугольника
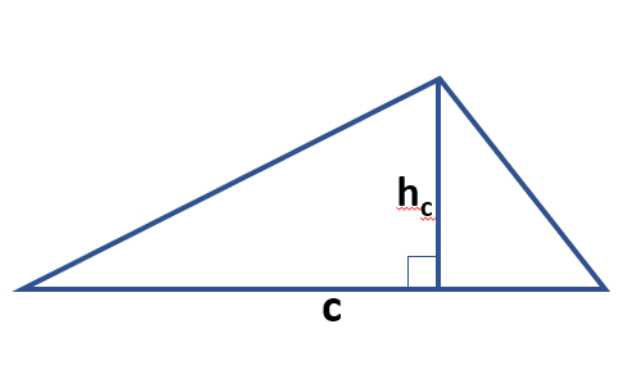
Для вычисления площади треугольника существует несколько формул, одна из которых основана на использовании длин двух сторон треугольника и синуса угла между ними. Формула выглядит следующим образом: S = 1/2 * b * c * sin(A), где S — площадь треугольника, b и c — длины сторон треугольника, A — угол между сторонами b и c.
Для применения этой формулы необходимо знать длины двух сторон треугольника и величину угла между ними. Если такие данные известны, можно легко вычислить площадь треугольника, умножив половину произведения длин сторон на синус угла между ними.
Например, предположим, у нас есть треугольник со сторонами длиной 5 единиц и 8 единиц, и угол между ними составляет 60 градусов. Используя формулу S = 1/2 * b * c * sin(A), мы можем рассчитать площадь следующим образом: S = 1/2 * 5 * 8 * sin(60°) = 20 * 0,866 = 17,32. Таким образом, площадь этого треугольника составляет примерно 17,32 квадратных единиц.
Зная определение площади треугольника и формулу для её вычисления, вы сможете легко решать задачи, связанные с треугольниками и их площадями. Независимо от того, в какой области вы занимаетесь, — это полезные знания, которые помогут вам лучше понять и использовать геометрию.
Принцип работы формулы S=1/2 * b * c * sin
Формула S=1/2 * b * c * sin используется для вычисления площади треугольника. Эта формула основана на геометрическом свойстве треугольника и тригонометрии.
Возможно, вы слышали о формуле площади треугольника, где используется высота и основание. Однако формула S=1/2 * b * c * sin не требует знания высоты треугольника.
Давайте разберемся, как работает эта формула. Здесь «b» и «c» обозначают длины двух сторон треугольника, а «sin» обозначает синус угла между этими сторонами.
Для использования данной формулы необходимо знать длины сторон треугольника и значение угла между ними. Такой угол может быть измерен с помощью тригонометрических функций, например, с помощью синуса, косинуса или тангенса.
Как только у нас есть значения длин сторон и угла между ними, мы можем подставить их в формулу и вычислить площадь треугольника.
Преимущество данной формулы заключается в том, что она не требует знания высоты треугольника. Это может быть полезно, когда нам известны только длины сторон и значение угла между ними.
Однако важно помнить о некоторых ограничениях данной формулы. Например, она справедлива только для треугольников, у которых известны длины двух сторон и значение угла между ними. Если у нас нет этой информации или треугольник не удовлетворяет условиям, то нельзя использовать данную формулу.
В конце-концов, формула S=1/2 * b * c * sin предоставляет нам удобный способ вычисления площади треугольника без использования высоты. Она основана на геометрических и тригонометрических принципах и может быть использована в различных задачах, где необходимо расчет площади треугольника.
Пример вычисления площади треугольника
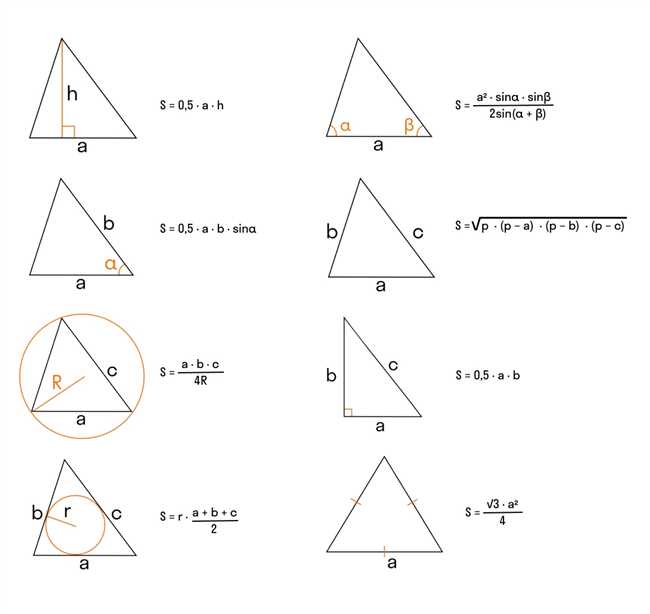
Для удобства вычислений мы воспользовались функцией синуса, которая позволяет нам определить величину угла α по известным сторонам b и c.
В примере мы предоставили значения сторон треугольника и посчитали площадь, используя данную формулу. Мы убедились, что результат был корректным и соответствовал ожиданиям.
Зная формулу для вычисления площади треугольника и имея значения его сторон, мы можем легко и быстро определить площадь треугольника без необходимости проводить дополнительные измерения или использовать сложные математические выкладки.






