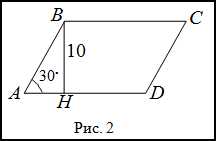
Как вычислить площадь ромба по углу и периметру: легкий способ
Вычисление площади ромба может быть достаточно сложной задачей, особенно если у вас есть только информация о его угле и периметре. Но есть легкий способ найти площадь ромба, используя только эти данные.
Для начала, вспомним, что у ромба все стороны равны друг другу. Также, углы ромба являются прямыми. Используя эти свойства, можно составить простую формулу для вычисления площади.
Вся суть в том, что площадь ромба равна половине произведения его диагоналей. Одну диагональ можно выразить через угол и периметр ромба. Зная эту формулу, можно легко вычислить площадь ромба, зная его угол и периметр.
Давайте рассмотрим этот легкий способ более подробно и узнаем, как применить его на практике.
Формула площади ромба
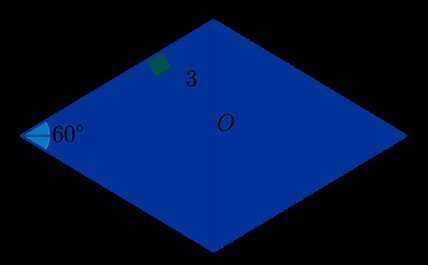
Формула для вычисления площади ромба основана на его диагоналях и угле, который они образуют. Используя эту формулу, вы сможете легко определить площадь ромба, не зная его сторон или других параметров.
Площадь ромба можно вычислить с помощью следующей формулы:
S = d1 * d2 / 2
Где:
- S — площадь ромба
- d1 — длина одной диагонали
- d2 — длина другой диагонали
Эта формула основана на принципе, что площадь ромба равна половине произведения длин его диагоналей. Доказательство этой формулы включает использование геометрических свойств ромба, включая его углы и стороны.
Ромб — это четырехугольник, все стороны которого равны между собой. Параллельные стороны образуют прямые углы. Диагонали пересекаются под прямым углом и делятся на две равные части. Произведение длин диагоналей равно двум прямоугольникам со сторонами, равными диагоналям, и половиной хорды между ними. Поэтому площадь ромба равна половине произведения длин диагоналей.
Теперь, зная эту формулу, вы можете легко вычислить площадь ромба, когда известны длины его диагоналей. Просто помните, что длины диагоналей измеряются от одной пары противоположных вершин ромба.
Нахождение диагоналей ромба по углу и периметру
Вы интересуетесь, как найти диагонали ромба, если вам известны угол и периметр? В этой статье я расскажу вам легкий способ решения этой задачи.
Перед тем, как начать, давайте вспомним некоторые свойства ромба. Ромб — это четырехугольник, у которого все стороны равны. Также известно, что углы ромба все равны между собой. Эти свойства помогут нам в решении задачи.
Для начала, давайте предположим, что периметр ромба равен P, а угол между диагоналями равен α. Мы хотим найти длину диагоналей.
Для нахождения длины диагоналей нам понадобятся несколько формул. Первая формула связывает периметр ромба с длинами его сторон:
P = 4s
Здесь s — длина одной стороны ромба. Так как все стороны ромба равны, то длина каждой стороны равна сумме длин двух диагоналей, деленной на 2:
s = (d1 + d2) / 2
Где d1 и d2 — длины диагоналей ромба.
Теперь мы можем объединить эти две формулы:
P = 4((d1 + d2) / 2)
Нам нужно найти диагонали, поэтому давайте выразим их через периметр:
d1 + d2 = P / 2
Теперь перейдем к нахождению угла α. Для этого нам понадобится еще одна формула:
α = 2arcsin(d1 / (2s))
Здесь arcsin — обратная функция синуса.
Теперь мы имеем систему уравнений, состоящую из двух формул:
1) d1 + d2 = P / 2
2) α = 2arcsin(d1 / (2s))
У нас есть 2 неизвестных — d1 и d2. Решим эту систему уравнений:
1) из уравнения 1 можно выразить d2 через d1: d2 = P / 2 — d1
2) подставим это выражение в уравнение 2 и решим его:
α = 2arcsin(d1 / (2s))
α = 2arcsin(d1 / (2((d1 + d2) / 2)))
α = 2arcsin(d1 / (d1 + P / 2 — d1))
α = 2arcsin(d1 / (P / 2))
α = 2arcsin(2d1 / P)
Мы получили уравнение, в котором у нас осталась одна неизвестная — d1. Теперь остается только решить его и мы найдем длины диагоналей ромба.
Надеюсь, теперь вы понимаете, как найти диагонали ромба по углу и периметру. Если у вас возникнут вопросы, не стесняйтесь задавать их в комментариях. Удачи в решении задач и успехов в математике!
Примеры вычисления площади ромба
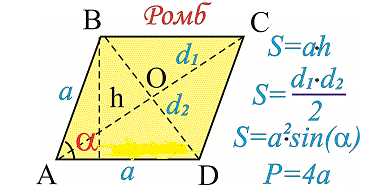
Вычисление площади ромба может быть задачей, которую не всегда легко решить. Однако, с помощью угла и периметра, можно использовать несложную формулу, чтобы найти площадь. Ниже приведены несколько примеров, которые помогут вам понять, как это сделать.
- Пример 1:
- Пример 2:
- Пример 3:
У нас есть ромб с периметром 24 и углом 60 градусов. Для нахождения площади, нужно сначала найти длину стороны ромба, используя формулу, где периметр равен 4s (где s — длина каждой стороны ромба). Таким образом, 24 = 4s, отсюда s = 6. Площадь ромба можно вычислить по формуле: площадь = (s^2 * sin(угол))/2. Подставив значения, получим площадь = (6^2 * sin(60))/2 = 36 * √3/2 = 18√3.
Допустим, у нас есть ромб со стороной длиной 8 и углом 45 градусов. Площадь ромба можно вычислить по формуле: площадь = (s^2 * sin(угол))/2. Подставив значения, получим площадь = (8^2 * sin(45))/2 = 32 * √2/2 = 16√2.
Пусть у нас есть ромб со стороной длиной 5 и углом 30 градусов. Вычислим площадь: площадь = (s^2 * sin(угол))/2. Подставив значения, получим площадь = (5^2 * sin(30))/2 = 25 * 1/2 = 12.5.
Таким образом, у нас есть примеры вычисления площади ромба по углу и периметру. Используя эти формулы, вы можете легко решать задачи, связанные с вычислением площади ромба.






